- •Раздел 1. Теория вероятностей
- •Тема 1. Случайные события
- •1.1.1.Предмет теории вероятностей
- •1.1.2.Вероятность события.
- •1.1.3.Действия над событиями
- •1.1.4.Формула полной вероятности
- •Тема 2. Случайные величины и законы их распределения
- •1.2.1. Понятие случайной величины
- •1.2.2. Функция распределения и плотность распределения
- •1.2.3.Числовые характеристики дискретных случайных величин
- •1.2.4. Непрерывные случайные величины (нсв), их числовые характеристики
- •Числовые характеристики непрерывных случайных величин
- •1.2.5. Закон больших чисел
- •Раздел 2. Математическая статистика
- •Тема 1. Выборочный метод
- •2.1.1. Задачи математической статистики
- •Тема 2. Статистическое оценивание и проверка гипотез. Статистические методы обработки экспериментальных данных
1.2.2. Функция распределения и плотность распределения
Функция распределения
Каждая случайная величина полностью определяется своей функцией распределения.
Если x .- случайная величина, то функция F(x) = Fx (x) = P(x < x) называется функцией распределения случайной величины x . Здесь P(x < x) - вероятность того, что случайная величина x принимает значение, меньшее x.
Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.
Функция распределения любой случайной величины обладает следующими свойствами:
F(x) определена на всей числовой прямой R;
F(x) не убывает, т.е. если x1
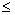 x2,
то F(x1)
F(x2);
x2,
то F(x1)
F(x2);F(-
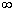 )=0,
F(+
)=1,
т.е.
)=0,
F(+
)=1,
т.е.
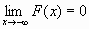 и
и
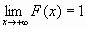 ;
;F(x) непрерывна справа, т.е.
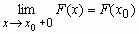
Плотность распределения
Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения: f (x) = F′(x).
Вероятность
того,что непрерывная случайная величина
Х примет значение, принадлежащее
интервалу (а,b), определяется равенством:
![]()
Зная
плотность распределения, можно найти
функцию распределения F(x)=
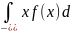 x
x
Плотность распределения обладает следующими свойствами:
Свойство 1. Плотность распределения неотрицательна, т.е. f(x) ≥0
Свойство
2. Несобственный интеграл от плотности
распределения в пределах от -
до +
равен единице:
![]() .
.
В
частности, если все возможные значения
случайной величины принадлежат интервалу
(a,b),
то
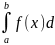 x=1
x=1
1.2.3.Числовые характеристики дискретных случайных величин
Математическое ожидание ДСВ
Математическим ожиданием (или средним значением) дискретной случайной величины называется сумма произведений всех её возможных значение на соответствующие им вероятности.
X |
|
|
… |
|
P |
|
|
… |
|
Т.е.,
если сл. величина имеет закон распределения,
то
![]()
называется
её математическим ожиданием. Если сл.
величина имеет бесконечное число
значений, то математическое ожидание
определяется суммой бесконечного ряда
![]() ,
при условии, что этот ряд абсолютно
сходится (в противном случае говорят,
что математическое ожидание не
существует).
,
при условии, что этот ряд абсолютно
сходится (в противном случае говорят,
что математическое ожидание не
существует).
Свойства математического ожидания
Свойство 1. Математическое ожидание постоянной равно самой этой постоянной.
Постоянная С принимает это значение с вероятностью единица и по определению М(С)=С×1=С
Свойство 2. Математическое ожидание алгебраической суммы случайных величин равно алгебраической суме их математических ожиданий.
Ограничимся
доказательством этого свойства только
для суммы двух дискретных случайных
величин, т.е. докажем, что
![]()
Под
суммой двух дискретных сл. Величин
понимается сл. Величина, которая принимает
значения
![]() с вероятностями
с вероятностями
По определению
![]()
![]()
Но,
![]()
где
![]() вероятность события
вероятность события
![]() ,
вычисленная при условии, что
,
вычисленная при условии, что
![]() .
В правой части последнего равенства
перечислены все случаи появления события
, поэтому
.
В правой части последнего равенства
перечислены все случаи появления события
, поэтому
![]() равна полной вероятности появления
события
, т.е.
равна полной вероятности появления
события
, т.е.
![]() Аналогично
Аналогично![]() . Окончательно имеем
. Окончательно имеем
![]()
Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
-
Y
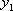
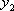
…
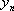
Q
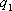
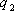
…
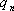
X
…
P
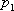
….
Приведем доказательства этого свойства только для дискретных величин. Для непрерывных случайных величин оно доказывается аналогично.
Пусть Х и У независимы и имеют законы распределения
Произведением
этих случайных величин будет случайная
величина, которая принимает значения
![]() с
вероятностями равными, в силу независимости
случайных величин,
с
вероятностями равными, в силу независимости
случайных величин,
![]() .
Тогда
.
Тогда
![]()
Следствие. Постоянный множитель можно выносить за знак математического ожидания. Так век постоянная С не зависит от того какое значение примет сл. величина X, то по свойству 3. имеем
М(СХ)=М(С)×М(Х)=С×М(Х)
Математическое ожидание числа появления события в схеме независимых испытаний.
Пусть
производится n
независимых опытов, вероятность
появления события в каждом из которых
равна Р. Число появлений события в этих
n
опытах является случайной величиною Х
распределённой по биномиальному закону.
Однако, непосредственное вычисление
её среднего значения громоздко. Для
упрощения воспользуемся разложением,
которым будем пользоваться в дальнейшем
неоднократно: Число появления события
в n
опытах состоит из числа появлений
события в отдельных опытах, т.е.
![]()
Где
![]() имеет закон распределения (принимает
значение 1, если событие в данном опыте
произошло, и значение 0, если событие в
данном опыте не появилось).
имеет закон распределения (принимает
значение 1, если событие в данном опыте
произошло, и значение 0, если событие в
данном опыте не появилось).
-
0
1
Р
1-р
р
Поэтому
![]()
Или
![]()
т.е. среднее число появлений события в n независимых опытах равно произведению числа опытов на вероятность появления события в одном опыте.
Например, если вероятность попадания в цель при одном выстреле равна 0,1, то среднее число попадания в 20 выстрелах равно 20×0,1=2.
Дисперсия ДСВ
Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
![]()
Для
вычисления дисперсии можно использовать
слегка преобразованную формулу
![]()
т.к.
М(х), 2 и
![]() постоянные величины, то
постоянные величины, то
![]()
![]()
Свойства дисперсии
Свойство 1. Дисперсия постоянной равна нулю. По определению
![]()
Свойство 2. Постоянную можно выносить за знак дисперсии с возведением в квадрат.
Доказательство:
![]()
Центрированной
случайной величиной называется отклонение
случайной величины от ее математического
ожидания.
![]()
Центрированная
величина обладает двумя удобными для
преобразования свойствами:
![]()
![]()
Свойство
3. Если случайные величины Х и У независимы,
то
![]()
Дисперсия числа появления события в схеме независимых испытаний
Производится
n независимых испытаний и вероятность
появления события в каждом испытании
равна р. Выразим, как и прежде, число
появления события Х через число появления
события в отдельных опытах
![]()
Так
как опыты независимы, то и связанные с
опытами случайные величины
независимы. А в силу независимости
имеем
![]()
-
0
1
Р
1-р
р
Но
каждая из случайных величин имеет закон
распределения и
![]() ,
поэтому по определению дисперсии
,
поэтому по определению дисперсии
![]()
Где q=1-p
В
итоге имеем
![]() ,
,
![]()
Среднее квадратическое отклонение
Дисперсия,
как характеристика разброса случайной
величины, имеет один недостаток. Если,
например, Х – ошибка измерения имеет
размерность ММ, то дисперсия имеет
размерность
![]() .
Поэтому часто предпочитают пользоваться
другой характеристикой разброса –
средним квадратическим отклонением,
которое равно корню квадратному из
дисперсии.
.
Поэтому часто предпочитают пользоваться
другой характеристикой разброса –
средним квадратическим отклонением,
которое равно корню квадратному из
дисперсии.
![]()
Среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.
Одинаково распределенные независимые случайные величины
Рассмотрим
n
взаимно независимых случайных величин
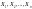 ,
которые имеют одинаковые распределения,
а
следовательно и одинаковые характеристики.
,
которые имеют одинаковые распределения,
а
следовательно и одинаковые характеристики.
Обозначим
среднее арифметическое рассматриваемых
случайных величин через


Математическое
ожидание среднего арифметического n
одинаково распределенных взаимно
независимых случайных величин равно
математическому ожиданию a
каждой из величин:
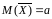
Дисперсия
среднего арифметического n
одинаково распределенных взаимно
независимых случайных величин в n
раз меньше дисперсии каждой из величин:
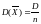
Среднее
квадратическое среднего арифметического
n
одинаково распределенных взаимно
независимых случайных величин в
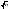 раз меньше среднего квадратического
каждой из величин:
раз меньше среднего квадратического
каждой из величин: