V. Для решения следующих задач используйте формулы для перестановок и сочетаний с повторениям

1. Найти число перестановок, образованных из всех букв слова комиссия.

2. Сколько различных перестановок можно образовать изо всех букв слова перестановка? Сколько из них начинается с буквы п и оканчивается буквой а?

3. Найти число всех возможных перестановок букв слова зоология. Сколько среди них таких, в которых три буквы о стоят рядом? Сколько таких, в которых в точности две буквы о стоят рядом?

4. Найти число различных способов, которыми можно выписать в один ряд 6 плюсов и 4 минуса.

5. Сколькими способами можно расположить в один ряд три красных мяча, четыре черных мяча и три белых мяча так, чтобы мячи, лежащие на краях, были одного цвета?

СЛОВАРЬ ТЕРМИНОВ

Combinatorics	Комбинаторика
Product rule	Принцип умножения
Sum Rule	Принцип сложения
Permutations	Размещение
Combinations	Сочетание
Arrangement	Расстановка
Repetitions	Повторение
Mutually exclusive	Взаимоисключающие
The order of the articles	Порядок элементов

Introduction

Combinatorics is the study of collections of objects. Specifically, counting objects, arrangement, derangement, etc. of objects along with their mathematical properties. Counting objects is important in order to analyze algorithms and compute discrete probabilities. Originally, combinatorics was motivated by gambling: counting configurations is essential to elementary probability.A simple example: How many arrangements are there of a deck of 52 cards? In addition, combinatorics can be used as a proof technique. A combinatorial proof is a proof method that uses counting arguments to prove a statement.

Product rule

If two events are not mutually exclusive (that is, we do them separately), then we apply the product rule.

Theorem (Product Rule)

Suppose a procedure can be accomplished with two disjoint subtasks. If there are ways of doing the first task and ways of doing the second, then there are

ways of doing the overall procedure.

Example 1

You are trying to construct a schedule. You have 3 courses you could take at 8:30, and 2 courses you could take at 9:30. How many different possible schedules are there?

Solution

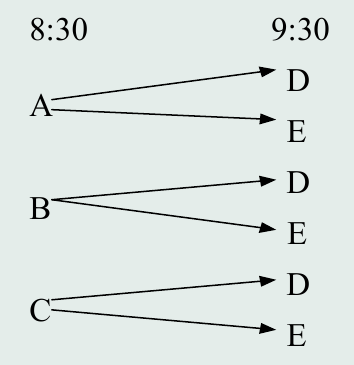
The answer is the product of 3 and 2, or 6. It is easy to see how this rule is derived, if you simply produce a diagram of the possibilities. Suppose that the available courses at 8:30 are labeled A, B, and C, and the available courses at 9:30 are D and E. You obtain 6 possible pathways, as

shown on the following picture.

Sum Rule

If two events are mutually exclusive, that is, they cannot be done at the same time, then we must apply the sum rule.

Theorem (Sum Rule)

If an event can be done in ways and an event can be done in ways and and are mutually exclusive, then the number of ways of both events occurring is

Example

If there are 3 different courses offered in the morning and 2 different course offered in the afternoon. There will be 3 + 2 choices for a student to enroll in only one course.

Permutations and Combinations

A combination of a given number of articles is a set or group of articles selected from those given where the order of the articles in the set or group is not taken into account.

A permutation of a given number of articles is a set or group of articles selected from those given where the order of the articles in the set or group is taken into account.

At that point we looked at straightforward questions and often used the formulae to calculate the number of permutations or combinations. We will now look at some more complicated examples where the formulae do not work directly.