Элементы комбинаторного анализа

Языковеду постоянно приходится решать задачи, в которых рассматриваются комбинации и расположения элементов, принадлежащих определенному лингвистическому множеству. Так, например, синтаксисту важно знать, сколько позиционных вариантов может давать в устно-разговорной речи предложение сегодня идет дождь. Фонетисту и специалисту в области кодирования текста нужно знать, сколько двухбуквенных, трехбуквенных и т.д. комбинаций может дать русский алфавит. Иногда при этом нужно выяснить, какая часть этих комбинаций образует слова и их формы, использующиеся в современном русском (английском или французском) языке. Задачи, в которых требуется ответить на вопрос «сколько?» или «сколькими способами?», называются комбинаторными, а раздел математики, занимающийся решением подобных задач, именуется комбинаторикой.

Комбинаторика (комбинаторный анализ, комбинаторная математика) – раздел математики, посвящённый решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами.

Например, путем перебора нетрудно установить, что предложение сегодня идет дождь имеет в русской разговорной речи 6 вариантов: сегодня идет дождь; сегодня дождь идет; дождь сегодня идет; дождь идет сегодня; идет сегодня дождь; идет дождь сегодня. Однако число комбинаций быстро растет с увеличением числа составляющих их элементов. Так, четыре слова (увы, сегодня, дождь, идет) дают 24, пять слов – 120, шесть – 720 позиционных вариантов и т. д. Не все из этих вариантов допустимы с точки зрения норм современного литературного языка. Определить допустимые варианты путем простого перебора оказывается зачастую невозможным. Поэтому, сталкиваясь с такими комбинаторными задачами, прибегают к типовым схемам решения, учитывающим лингвистические или какие-либо другие ограничения.

Принцип умножения. Пусть необходимо выполнить одно за другим какие-то k действий. Если первое действие можно выполнить n₁ способами, после чего второе действие можно выполнить n₂ способами, после чего третье действие можно выполнить n₃ способами, и так далее до k-го действия, которое можно выполнить n_k. способами, то все k. действий вместе могут быть выполнены n_{1 *} n_{2 *} n_{3 *} ... _* n_k способами.

Принцип сложения. Если два действия взаимно исключают одно другое, причем одно из них можно выполнить m способами, а другое — n способами, то какое-либо одно из них можно выполнить m+n способами.

Пример. В магазине имеется три разных коробки шоколадных конфет и четыре вида плюшевых медведей, то подарить девушке что-нибудь одно (конфеты или медведя) можно семью различными способами, а составить подарок из плюшевого медведя и коробки конфет можно двенадцатью различными способами.

1. Размещения. Предположим, что имеется алфавит, включающий п элементов. Из этих элементов составляются m-членные комбинации (соединения), причем каждый из п элементов может входить в соединение не более одного раза.

Т акой тип комбинаций называется размещением. Число размещений из п элементов по т определяется по формуле:

П ример. Из 32 букв русского алфавита можно составить

двухбуквенные комбинации, не содержащие повторений букв. По данным четырехтомного «Словаря русского языка» (М., 1957–1961), из этих сочетаний только 114 выступает в качестве самостоятельных слов (имена собственные, сокращения, архаизмы и диалектные слова при этом не учитываются).

2. Размещения с повторениями. Снова возьмем алфавит из п элементов и будем составлять m-членные соединения, допуская повторения каждого элемента от 0 до m раз. Тогда общее число соединений, называемых размещениями с повторениями, находится по формуле

П ример. Из 30 букв русского алфавита (исключая ь и ъ) можно составить 30² = 900 двухбуквенных серий (например, для денежных знаков) и 30³ = 27 000 трехбуквенных серий.

3. Перестановки. Пусть размещения из п разных элементов взяты по п элементов, т.е. каждое размещение содержит все п элементов алфавита и отличается от других лишь порядком этих элементов. Такие размещения называются перестановками. Для нахождения числа перестановок используют формулу P_n = n!

4. Перестановки с повторениями. В тех случаях, когда среди образующих перестановки элементов имеются одинаковые, получаются соединения, называемые перестановками с повторениями. Число этих перестановок вычисляется по формуле

Pⁿ_{n1 , n2 , ... nk} = , где п — общее количество элементов, входящих в перестановку, a n₁, n₂,, n_k — количество одинаковых элементов в первой, второй, ..., k-й группах.

Пример. Определим число перестановок с повторениями, которое можно получить из букв, составляющих словоформу математика. Всего в перестановках участвует десять букв, т. е. n = 10; буква м повторяется два раза, поэтому если бы все остальные буквы были различными, то искомое число перестановок, было бы равно P₂¹⁰= 10! / 2!. На самом деле, кроме двух одинаковых м в нашем слове имеются три а и два т. Поэтому общее число перестановок, полученных из букв, входящих в словоформу математика, равно

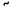P¹⁰_2,2,3⁼

5 . Сочетания. В размещениях из n элементов по m соединения отличаются друг от друга либо элементами, либо их порядком, либо и элементами и их порядком. Объединим в отдельные группы такие комбинации, Объединим в отдельные группы такие комбинации, которые содержат т одинаковых элементов и отличаются друг от друга только порядком этих элементов. Нетрудно заметить, что в каждой группе будет ровно Р_т элементов. Группы комбинаций, различающиеся только элементами, называются сочетаниями из п элементов по т. Их число равно

6. Сочетания с повторениями. Сочетаниями из п элементов по т с повторениями называются такие соединения, которые включают т из п различающихся между собой элементов при условии, что один и тот же элемент может включаться в комбинацию несколько раз. Два соединения считаются различными, если они отличаются хотя бы одним элементом, и одинаковыми, если они состоят из одних и тех же элементов. Число сочетаний из п элементов по т с повторениями определяется по формуле