Расчет бункеров. Определение давления на стенки бункеров.

Давление груза на стенки бункера зависит от свойств груза и конфигурации бункера. Наиболее просто его определить для грузов, по свойствам близких к жидкостям. В этом случае давление на стенки распреде­ляется по гидростатическому закону

σ = h γ n_д,

где h — глубина расположения точки приложения давления;

n_д — поправочный коэффициент, учитывающий динамичность нагрузки; n_д = 1 + j/g (здесь j — наибольшее ускорение вертикальных колебаний бункера). Обычно не пре­вышает 6 м/с². Это значение и следует считать расчетным, если точное значение неизвестно.

Коэффициент динамичности для транспортных бункеров n_д = 1,6, для неглубоких бункеров с вибраторами k_д = 1,3...1,5. Если груз падает в неглубокий бункер с большой высоты (напри­мер, при загрузке грейфером), то k_д = = 1,1...1,4. Если фундаменты неглубоких бункеров подвергаются сотрясениям (например, при расположении их вблизи копров и т. п.), то k_д = 1,1...1,2.

Для глубоких бункеров коэффициент динамич­ности можно приближенно вычислить по формуле k_д = 0,65+ 0,35·h_CT /А_б,

где h_CT > A_б — высота стенок бункера.

Давление сыпучих грузов на стенки бункеров зависит от сил внутреннего трения и сцепления частиц груза. При расчете давле­ния сыпучих грузов на стенки бункеров исходят из следующих допущений:

- сыпучий груз состоит из частиц столь малых, что размерами их по сравнению с размерами бункера можно пренебречь и рассма­тривать сыпучий груз как сплошную среду;

- между частицами груза могут действовать силы трения, макси­мальное значение которых пропорционально нормальному давле­нию;

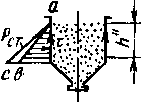
Схема для расчета давления

груза на стенки бункера

- между частицами груза могут возникнуть силы сцепления, не зависящие от давления.

В бункере наблю­дается вертикальное перемещение глубоко расположенных слоев материала под давлением верхних слоев и возникает упругая дефор­мация стенок бункера. На поверхности стенок бункера начинают дейст­вовать направленные вверх касательные напряжения, воспринимающие частично вес содержимого бункера. В результате распределение давлений будет откло­няться от гидростатического закона тем сильнее, чем больше глубина погружения.

Общее выражение давления на вертикальные стенки имеет вид

σ = n_Д ε K h γ,

где ε — коэффициент, учитывающий вертикальные силы трения насыпного груза о стенки бункера (так называемый коэффициент зависания):

здесь χ = (K h f1) / R_Б

f1 — коэффициент трения насыпного груза о стенки бун­кера;

R_Б — гидравлический радиус бункера, равный частному от деления площади горизонтального сечения бункера на его периметр;

Для неглубоких бункеров ε = 1

К — коэффициент боко­вого давления, равный отношению боко­вого давления к вертикальному, зависит от глубины бункера (у глубоких бункеров высота вертикальных стенок превышает ширину бункера). Для неглубоких бункеров коэффициент боко­вого давления принимают равным коэффициенту подвижности.

Для глубоких бункеров коэффициент бокового давления:

для круглых и квадратных

для щелевых бункеров

f — коэффициент внутреннего трения груза.

При определении давления груза на вертикальные стенки расчетную величину h находят по разному для открытых бункеров. Открытый бункер может быть загружен с «шапкой», в этом случае расчетная высота h будет больше, чем высота h_ст стенок.

При загрузке круглого бункера в центральной точке «шапка» имеет вид конуса и высота h определяется по формуле

h" = h_ст + А_бf/6.

При загрузке щелевого бункера по центральной линии (на­пример, с помощью передвижной сбрасывающей тележки ленточ­ного конвейера) расчетную высоту h" определяют по формуле h" = h_ст + А_бf/4.

На наклонные стенки давление хорошо сыпучих грузов неглу­боких бункеров

σ_н = n_д h γ (cos² α + m sin² α),

где β — угол наклона стенок к горизонтали;

m— коэффициент подвижности груза.

(ПСМ) При больших значениях начального сопротивления сдвигу уточняют значение давления на вертикальные стенки по выраже­нию

р = n_д ε K (h – h0) γ,

где h₀ — высота вертикальной свободностоящей стенки;

Коэффициент зависания ε определяют по формуле при значении

χ = K (h – h₀)f1 / R_Б.

Давление на наклонные стенки неглубоких бункеров, содер­жащих плохосыпучие грузы,

σ_н = n_д γ [hcos²α + m(h - h₀) sin²α].

Если глубина h < h₀, то

σ_н = n_д γ h cos²α.

Давление грузов на наклонные стенки днища глубоких бункеров

σ_н = n_д γ [ε(h – h₀)(cos²α + К sin²α) + h₀ cos²α].

Коэффициент К определяют как для хорошо сыпучих грузов

Коэффициент зависания находят по максимальному гидрав­лическому радиусу днища.

По формуле можно вычис­лить и давление грузов на горизонтальные днища глубоких бун­керов при β = 0. формула применима и для расчета бункеров для хорошо сыпучих грузов при h₀ = 0.

Расчет круглых бункеров

Определение действующих расчетных усилий. Обозначим че­рез Nс усилие, действующее вдоль образующей конуса (скатное усилие), и через Nк — кольцевое усилие, действующее на расстоянии у от вершины конуса.

Скатное растягивающее усилие, отнесен­ное к единице длины окружности радиуса R (см. рис. 46, а), определяют по формуле

г де σв — вертикальное давление груза; G_B — вес груза, содержа­щегося в бункере ниже рассматриваемого сечения cd (см. рис.), и собственный вес отсеченной нижней части бункера; α — угол наклона стенки к горизонту.

Кольцевое усилие Nк, отнесенное к единице длины образующей бункера, вычисляют по формуле

С 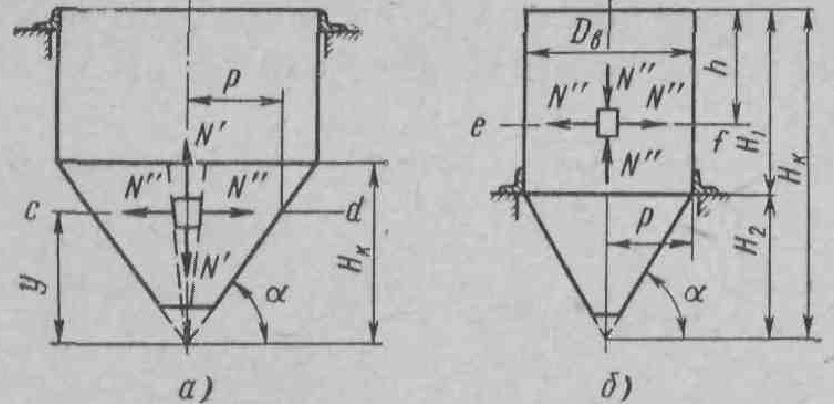хемы к расчету на проч­ность круглых бункеров

Приведенные формулы при подстановке а = 90° действительны для расчета цилиндрической части, если она расположена ниже опорного кольца бункера.

Е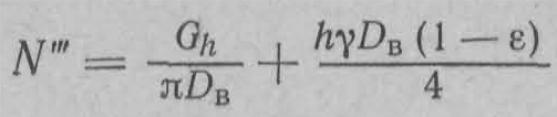 сли же цилиндриче­ская часть бункера расположена выше опорного кольца, то в вертикальных стенках вместо растягивающих усилий Nс возникают сжимающие усилия Nс' (отнесено к еди­нице периметра бункера)

где G_h — собственный вес части бункера, расположенной выше рассматриваемого сечения ef (см. рис. 46, б); h — расстояние от верхних кромок бункера до рассматриваемого сечения; e — коэф­фициент зависания.

Толщину стенок цилиндрической части цилин-дроконических бункеров с опорой внизу, определяют по формуле

, (126)

где — боковое давление на уровне рассматриваемого горизонтального сечения; — диаметр бункера.

Если цилиндроконический бункер подвешен за верхнюю окантовку (см. рис. 46, а), то толщину стенок цилиндрической части , полученную по формуле (126), следует проверить на растяжение в вертикальном направлении под действием полного веса загруженного бункера.

Напряжение растяжения а, возникающее в стенках конических бункеров под действием усилия Nс находят по формуле

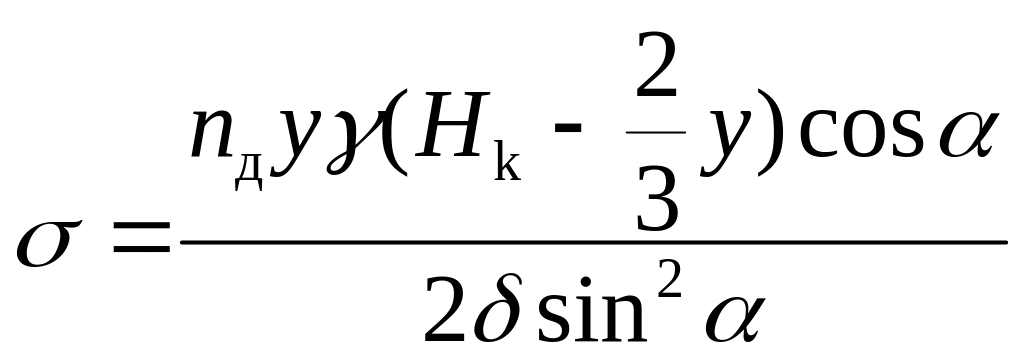, (122)

где у — расстояние рассматриваемого сечения от вершины конуса (см. рис, 46, а); — коэффициент динамичности; — толщина стенки бункера; — высота конуса.

Напряжение достигает максимума при . Максимальное напряжение

. (123)

Кольцевое напряжение под действием усилий Nк [формула (120)] определяют по формуле

, (124)

где т' — коэффициент подвижности

При напряжение достигает максимума

. (125)

Напряжения в стенках конической части (воронке) неглубокого цилиндроконического бункера находят по формулам (122) и (124), если под величиной Н_к понимать высоту бункера (см. рис; 46, б) от верхних кромок до вершины конуса. Вид формул для расчета максимальных значений , зависит от соотношения высот цилиндрической и конической частей бункера и (рис. 46, б).

Формула (123) справедлива при ; если , то следует пользоваться формулой

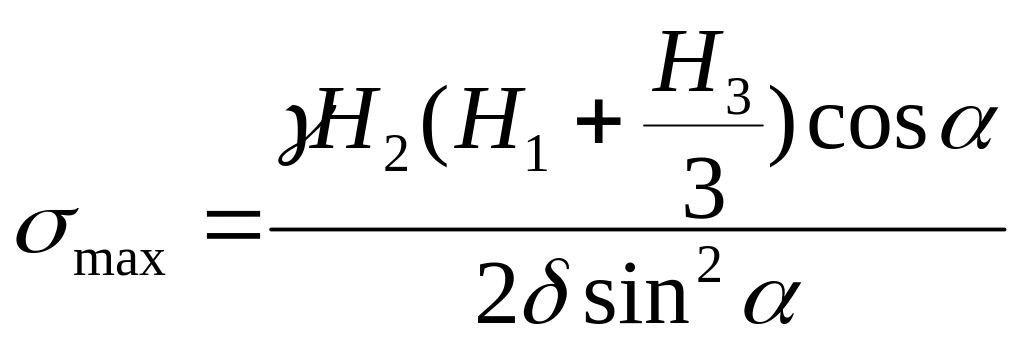. (127)

Формула (125) справедлива при . Если , то

. (128)

По формулам (122—128) можно рассчитать стенки бункеров для легкосыпучих грузов; их можно применять также для расчета бункеров с полужидкими грузами при т'= 1.

По этим же формулам можно рассчитывать бункеры с плохо-сыпучими грузами; получаемая при этом погрешность будет в сторону запаса прочности.

РАСЧЕТ НА ПРОЧНОСТЬ ПРЯМОУГОЛЬНЫХ БУНКЕРОВ

На прочность стенок подвесных стальных бункеров влияют возникающие растягивающие и изгибающие напряжения. Общая картина действия сил показана на рис. 45, а, б.

В верхних вертикальных стенках бункера, опирающихся на колонны (рис. 45, а), действуют горизонтальные растягивающие усилия N_a, N_B. Стенки работают еще на местный изгиб под действием бокового давления груза как пластины и на общий изгиб под действием собственного веса как балки.

В наклонных стенках воронки кроме перечисленных нагрузок действуют еще и растягивающие силы вдоль ската воронки (скатные усилия).

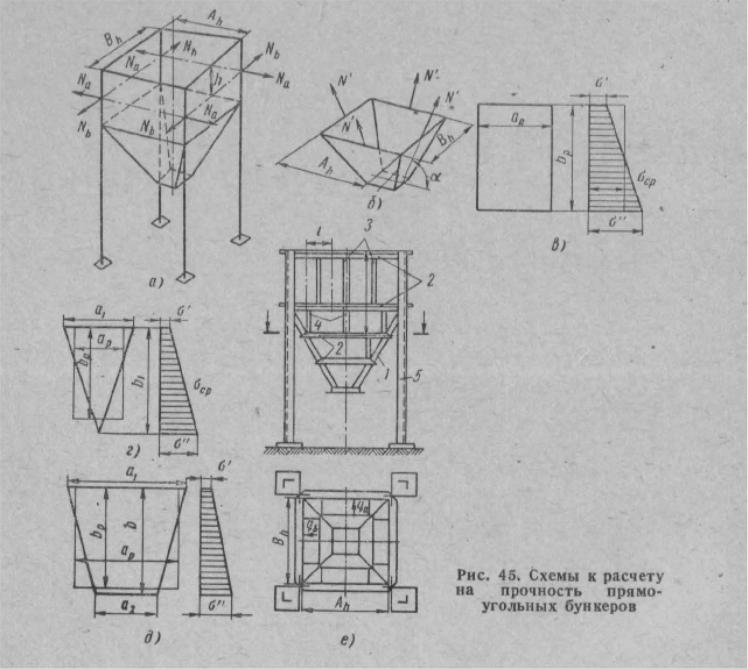
Если бункер подвешен за верхнюю окантовку вертикальных стенок (это встречается сравнительно редко), то в вертикальных стенках могут возникнуть вертикальные растягивающие силы.

Определение, растягивающих усилий. Горизонтальные растягивающие усилия, отнесенные к единице линейного размера стенок по высоте, вычисляют по формулам

N_a = σB_h /2; N_B= σA_h/2, (98)

где σ — боковое давление; A_h, B_h— размеры поперечного сечения бункера на рассматриваемом уровне.

Величину скатных усилий N' (рис. 45, б), отнесенных к единице периметра стенок, при симметричной форме воронки определяют по формуле

, (99)

где G"— вертикальная нагрузка на рассматриваемое сечение воронки; α — угол наклона стенки к горизонту.

Вертикальную нагрузку G" находят по формуле

G" = A_hB_hσ + G_B, (100)

где σ — вертикальное давление груза; G_B — вес груза, содержащегося в воронке ниже рассматриваемого сечения, а также собственный вес нижней части воронки.

Определение изгибающих моментов. Наибольший изгибающий момент, возникающий в стенках, имеющих опору по контуру, под действием давления насыпного груза, вычисляют по формуле

М_max = , (101)

где σ_cp— среднее нормальное давление насыпного груза на стенку; a_p < b_p — расчетные размеры пластины (рис. 45, в); с₁ — безразмерный коэффициент (см. табл. 1)

_{1. Значения коэффициента c}1

Отнош	Коэффициент c1		Отнош	Коэффициент c1
сторон, bp/ ap	зажат	опоры	сторон, bp/ ap	зажат	опоры
1	19,5	20,9	2	12,1	9,8
1,2	15,6	16	3	12	8,4
1,4	13,7	13,3	4	12	8,1
1,6	12,7	11,6	∞	12	8
1,8	12,2	10,6

Среднее давление σ_cp [см. формулу (101)] вычисляют для наклонных и вертикальных стенок стальных бункеров.

Для прямоугольной пластины

σ_cp= , (102)

где σ', σ" — наименьшая и наибольшая величины нормальных давлений (рис. 45, в, д).

Для треугольной пластины (рис. 45, г)

σ_cp= . (103)

Для трапецеидальной пластины (рис. 45, д)

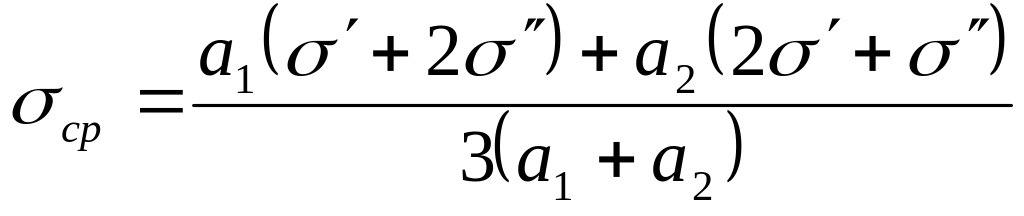, (104)

где а₁, а₂ — верхнее и нижнее основания трапеции.

Расчетные размеры а_p, b_p, входящие в формулу (101), для треугольных и трапецеидальных пластин определяют путем условного преобразования их формы в прямоугольную.

Для треугольных пластин расчетные размеры вычисляют по формулам

; , (106)

где а₁, b₁ — основание и высота треугольника (рис. 45, г).

Для трапецеидальных пластин (см. рис. 45, г) расчетные размеры находят по формулам:

; , (107)

где b₁ — высота трапеции.

Расчет стенок металлических бункеров. Конструкция стенок металлических бункеров состоит из каркаса и обшивки. Каркас бункера — из профильного проката; элементы каркаса носят название ребер.

Различают ребра (рис. 45, е): угловые 1, горизонтальные 2, вертикальные 3 и ребра, идущие вдоль ската воронки — 4 (скатные).

Стальные листы обшивки бункера рассчитывают на местный изгиб, возникающий под воздействием давления насыпного груза на стенки

δ= , (108)

где δ — толщина листов обшивки, см; с₁ — коэффициент (находят по табл.1); σ_доп — допустимое давление на стенки.

При жестком соединении угловых ребер 1 с колоннами 5 (см. рис. 45,е) ребра рассчитывают на растяжение под действием усилий N, которые определяют по приближенной формуле

N= , (109)

где G" — вертикальная нагрузка [вычисляют по формуле (100) для верхнего сечения воронки]; θ — угол наклона углового ребра к горизонту [определяют по формуле (103)]; k_H — коэффициент неравномерности распределения нагрузки.

Для симметричных воронок k_H = 1. Для несимметричных -1,6.

Если бункер подвешен за верхнюю окантовку вертикальных стенок, то боковые ребра подобно скатным рассчитывают на растяжение под действием удельных скатных усилий, определяемых по формулам (99). Усилие, приходящееся на отдельное ребро, рассчитывают по формуле

N = Nс l', (110)

где l' — ширина участка стенки, условно отнесенного к данному ребру (обычно l' определяют как расстояние между серединами смежных листов обшивки, примыкающих к рассчитываемому ребру).

Скатные ребра, кроме того, рассчитываются на изгиб под действием давления насыпного груза на стенки. Изгибающий момент находят по формуле

М = , (111)

где q_H — интенсивность равномерно распределенной нагрузки; l — пролет ребра; с₂ — безразмерный коэффициент (с₂ = 8 для балки со свободно лежащими концами; с₂ = 12 при защемленных концах).

Интенсивность нагрузки [см. формулу (111)]

q_H = σl', (112)

где σ — давление на стенки, определяемое на уровне средней точки ребра по высоте; l' — то же, что и в формуле (110).

Суммарное напряжение в растянутых волокнах скатных ребер

(113)

где N — растягивающее усилие; М — изгибающий момент; F — площадь поперечного сечения ребра; W — момент сопротивления ребра.

Величина напряжения не должна превышать величины [см. формулу (108)].

Если призматическая часть бункера опирается на колонны, то вертикальные ребра 3 (см. рис. 45, в) рассчитывают только на изгиб, причем изгибающий момент определяют так же, как и для скатных ребер, по формуле (111). В случае подвески бункера за верхнюю окантовку призматической части вертикальные ребра рассчитывают на изгиб и на растяжение усилием N, которое находят по формуле

, (114)

где — вес бункера с его содержимым; , — размеры горизонтального сечения призматической части бункера; — то же, что и в формуле (110).

Суммарное напряжение вертикальных ребер определяют по формуле (113).

Горизонтальные ребра каркаса рассчитывают на растяжение под действием сил и (см. рис. 45, б), которые находят по формулам (98), и на изгиб под действием давления насыпного груза на стенки. Обычно горизонтальные ребра жестко соединены в углах и образуют замкнутую раму. Узловые изгибающие моменты рамы определяют по формуле

, (115)

где A_h, B_h — размеры ребер (см. рис. 45, е); , — интенсивность равномерного распределения нагрузок на ребра.

Пролетные изгибающие моменты определяют по формулам

; , (116)

Интенсивность нагрузок q_a, q_b, входящих в приведенные формулы, находят по формулам

; , (117)

где — давление на стенки, определяемое на уровне рассматриваемого ребра; , — углы наклона стенок бункера в зоне горизонтальных ребер с длинами A_h и B_h соответственно.

Рассчитывают ребра на изгиб либо по узловому моменту, либо по пролетному в зависимости от того, который из этих моментов больше.

Если горизонтальные ребра не имеют жесткой связи в углах, то изгибающие моменты определяют по формулам

; , (118)

Суммарное напряжение в горизонтальных ребрах вычисляют по формуле (113).