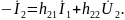- •8 Теорема об эквивалентном генераторе
- •1.9 Преобразование реального источника напряжения в реальный источник тока
- •1.10 Преобразование треугольника сопротивлений в эквивалентную звезду
- •1.11 Преобразование звезды сопротивлений в эквивалентный треугольник
- •2.2 Разряд и заряд конденсатора через резистор
- •2.3 Конденсатор в цепи переменного синусоидального тока
- •2.5 Переходные процессы в цепях с катушкой индуктивности
- •2.6 Катушка индуктивности в цепи переменного
- •2.7 Использование комплексных чисел при расчете электрических цепей переменного синусоидального тока
- •1. Параллельное соединение и
- •2. Последовательное соединение и
- •2.10 Мощность цепи переменного синусоидального тока
- •Баланс мощности в сложных
- •Метод контурных токов
- •Метод узловых потенциалов
- •Метод двух узлов
- •2. Несинусоидальные периодические токи.
- •3. Максимальные, средние и действующие значения
- •4. Расчет цепей при несинусоидальных эдс и токах.
- •5. Мощность цепи несинусоидального тока
- •3. Каскадное соединение четырехполюсников
- •2. Классический метод расчета переходных процессов
- •3. Переходные процессы в цепях синусоидального тока
- •4. Операторный метод расчета переходных процессов
- •5. Свойства (теоремы) преобразования Лапласа
- •1 Принцип построения трехфазной системы
- •2. Соединение звездой
- •3. Соединение треугольником
- •4. Мощность в трехфазных цепях
- •1. Основные определения
- •2. Свойства ферромагнитных материалов
- •3. Расчет магнитных цепей
- •4. Трансформатор
- •4.1. Устройство
- •4.2. Холостой ход
- •4.3. Режим нагрузки
- •4.4. Пример
4. Расчет цепей при несинусоидальных эдс и токах.
1. Заданная несинусоидальная ЭДС раскладывается на гармонические составляющие.
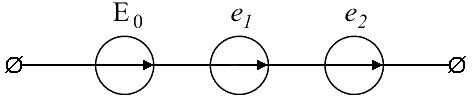
Например:
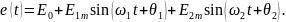
2. В соответствии с принципом наложения производится расчет токов и напряжений на участках при действии каждой ЭДС в отдельности. При расчете следует учитывать, что реактивные сопротивления зависят от частоты:

Если источник несинусоидальной ЭДС подключается непосредственно к емкости, то ток в ней:

где
 .
.
Отсюда следует, что в индуктивности несинусоидальность тока меньше, чем у напряжения. Расчет цепи для каждой из гармоник в отдельности может производиться символическим методом и любыми другими, на нем основанными.
3. Результаты расчета рассматриваются совместно. При этом мгновенное значение любой величины определяется как сумма мгновенных значений составляющих гармоник. Например, для тока:
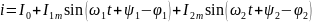 ,
,
а его действующее значение
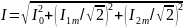 .
.
При задании источников токов принцип решения остается тем же.
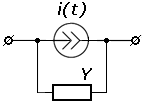
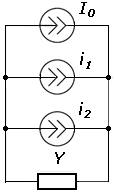
Источник несинусоидального тока представляется в виде параллельного соединения ряда источников гармонического тока:

Билет 18
5. Мощность цепи несинусоидального тока
Активная мощность цепи несинусоидального тока определяется так же, как для цепи синусоидального тока, т.е. как среднее значение мгновенной мощности за период:
|
(4) |
Подставляя в (4) выражения для напряжения и тока, получим:
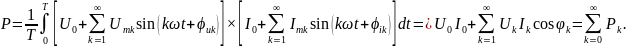
Таким
образом, активная мощность при
несинусоидальном токе равна сумме
активных мощностей отдельных гармоник,
включая постоянную составляющую, как
гармонику с нулевой частотой (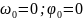 ).
).
По аналогии с синусоидальным током можно ввести понятие реактив-
ной мощности, как суммы реактивных мощностей гармонических составляющих, т.е.
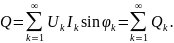
Также по аналогии вводится понятие полной мощности, как произведение действующих значений напряжения и тока
 .
.
Необходимо отметить, что при несинусоидальных токах

причем равенство достигается, только при синусоидальных токах.
Отношение
активной мощности к полной называется
коэффициентом мощности и его можно
приравнять косинусу некоторого угла
 ,
т.е.
,
т.е.
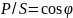 .
.
Билет 19
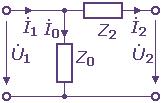
А - Форма уравнений четырехполюсника
Участок электрической цепи, который имеет два входных и два выходных полюса (зажима), называется четырехполюсником.
Четырехполюсники бывают активными (с источниками ЭДС внутри) и пассивными.
К активным четырехполюсникам относятся различные усилители, схемы, содержащие источники энергии. Пассивными четырехполюсниками являются трансформаторы, линии электропередач, пассивные фильтры и др.
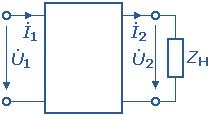
На схеме замещения четырехполюсник обозначается прямоугольником.
Четырехполюсник может быть симметричным, если при изменении входных полюсов выходными режим работы внешних цепей не изменяется. В других случаях четырехполюсник является несимметричным.
|
На
рисунке 1 приведен пассивный
четырехполюсник. Различают входное
и выходное сопротивления четырехполюсника:
где
|
Рисунок 1 |
Взаимные сопротивления определяются так:
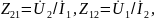
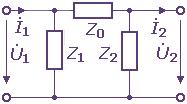
Если взаимные сопротивления равны, то пассивные четырехполюсники обратимы. Любой пассивный четырехполюсник может отвечать схемам замещения: Т -, П -, Г-образной (рисунок 2).
|
|
|
Рисунок 2 |
||
Можно доказать, что в каждой из приведенных схем между напряжением и током приемника и напряжением и током источника существует линейная зависимость.
Если рассмотреть Т-образную схему, то по первому закону Кирхгофа

а учитывая, что

можно получить зависимость

Напряжение на входе четырехполюсника по уравнению второго закона Кирхгофа
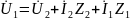
Если
учесть зависимость для тока
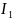 ,
то можно получить
,
то можно получить
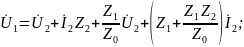
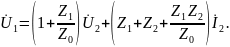
Следовательно, в основных уравнениях четырехполюсника входные и выходные величины связаны линейно
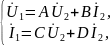
где
А,
B, C, D
 коэффициенты четырехполюсника, которые
определяются таким образом:
коэффициенты четырехполюсника, которые
определяются таким образом:
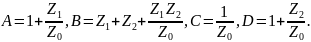
Всегда справедливо соотношение коэффициентов
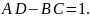
Коэффициенты четырехполюсника можно определять экспериментальным путем по исследованиям холостого (нерабочего) хода и короткого замыкания. В этом случае уравнения четырехполюсника имеют такой вид:
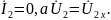
В опыте холостого хода
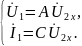
При коротком замыкании, а уравнения

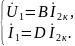
Коэффициенты четырехполюсника имеют смысл:
|
|
|
Билет 20 |
2. H - ФОРМА УРАВНЕНИЙ ЧЕТЫРЕХПОЛЮСНИКА
Эта
форма записи уравнений находит широкое
распространение в электронике. h
-параметры устанавливают зависимости
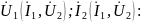
|
(1) |
|
(2) |
Для определения h-параметров используют результаты расчетов режимов холостого хода и короткого замыкания.
При
коротком замыкании ( )
согласно (1),
(2)
)
согласно (1),
(2)

При
холостом ходе
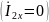 :
:
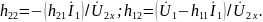
Схема замещения четырёхполюсника в h-параметрах приведена на рисунке 3.
|
Рисунок 3 |
Параметр
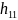 соответствует
входному сопротивлению четырёхполюсника,
его выражают в Омах. Параметр
соответствует
входному сопротивлению четырёхполюсника,
его выражают в Омах. Параметр
 имеет размерность проводимости (См).
Параметр
имеет размерность проводимости (См).
Параметр
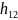 –
безразмерная
величина. Параметр
–
безразмерная
величина. Параметр
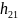 –
безразмерная величина, соответствующая
коэффициенту усиления по току.
–
безразмерная величина, соответствующая
коэффициенту усиления по току.
Билет 21

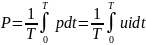

 – входное сопротивление;
– входное сопротивление; – выходное сопротивление четырехполюсника.
– выходное сопротивление четырехполюсника.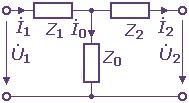
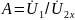 – величина,
обратная коэффициенту усиления по
напряжению;
– величина,
обратная коэффициенту усиления по
напряжению;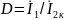 – величина,
обратная коэффициенту усиления по
току;
– величина,
обратная коэффициенту усиления по
току;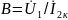 – передаточное
сопротивление при замкнутых выходных
зажимах;
– передаточное
сопротивление при замкнутых выходных
зажимах;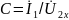 – передаточная
проводимость при разомкнутых выходных
зажимах.
– передаточная
проводимость при разомкнутых выходных
зажимах.