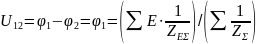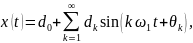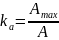3. Метод двух узлов

Схема на рисунке 4 имеет два узла.

	Составим узловое уравнение для узла 1: , Потенциал точки 2 примем равным нулю: = 0. , В общем виде:
Рисунок 4

В знаменателе формулы – сумма проводимостей параллельно включенных ветвей. В числителе – алгебраическая сумма произведений ЭДС источников на проводимости ветвей, в которые эти ЭДС включены. ЭДС в формуле записывается со знаком "плюс", если она направлена к узлу 1, и со знаком "минус", если направлена от узла 1.После вычисления величины потенциала находим токи в ветвях.

Билет 15

2. Несинусоидальные периодические токи.

Для анализа цепей при несинусоидальных периодических токах применяется разложение функции в тригонометрический ряд Фурье. Пусть ток или напряжение описывается периодической функцией , которая удовлетворяет условиям Дирихле, т.е. является кусочно-непрерывной, кусочно-монотонной в пределах периода , а в точках разрыва принимает конечные значения. Такую функцию можно представить в виде ряда Фурье:

		(1)
где
k	– номер гармонической составляющей
	– круговая частота периодического сигнала,
	– постоянная составляющая (среднее значение) сигнала,
	– амплитуды косинусоидальных составляющих сигнала,
	– амплитуды синусоидальных составляющих сигнала.

_{Ряд Фурье (1) можно так же представить в виде}

		(2)
где

Разложения в ряд прямоугольной и треугольной функций:

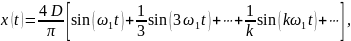
где

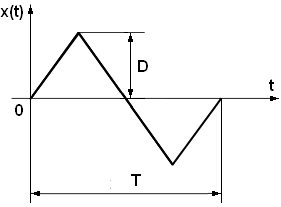
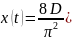
где

Билет 16

3. Максимальные, средние и действующие значения

несинусоидальных токов.

Под максимальным значением 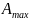понимают наибольшее значение функции за период.

Среднее значение определяется как среднее по модулю:

В случае, если за весь период функция ни разу не меняет знака, среднее по модулю значение равно постоянной составляющей.

Обычно в расчетах пользуются действующим значением ЭДС, токов, и напряжений, которые определяются по формуле:

Разложив заданную функцию в ряд и подставив в выражение для действующего значения, получим:

Возведение ряда в квадрат здесь возможно, так как ряд абсолютно сходится при любом значении .

Окончательно

(3)

Для токов, ЭДС и напряжений:

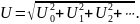
В электроэнергетике, где кривые обычно симметричны относительно оси абсцисс, для оценки несинусоидальности пользуются:

коэффициентом формы:

(для синусоиды

)

коэффициентом амплитуды:

(для синусоиды

)

коэффициентом искажения:

(для синусоиды

)

По стандарту напряжение промышленной сети считается практически синусоидальным, если действующее значение всех высших гармоник не превышает 5% действующего значения напряжения основной частоты. Коэффициент искажения такой кривой с точностью до долей процента равен единице.

В электронике и радиотехнике для оценки искажений пользуются коэффициентом гармоник:

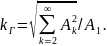
Билет 17
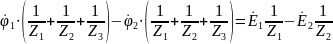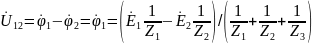