
- •8 Теорема об эквивалентном генераторе
- •1.9 Преобразование реального источника напряжения в реальный источник тока
- •1.10 Преобразование треугольника сопротивлений в эквивалентную звезду
- •1.11 Преобразование звезды сопротивлений в эквивалентный треугольник
- •2.2 Разряд и заряд конденсатора через резистор
- •2.3 Конденсатор в цепи переменного синусоидального тока
- •2.5 Переходные процессы в цепях с катушкой индуктивности
- •2.6 Катушка индуктивности в цепи переменного
- •2.7 Использование комплексных чисел при расчете электрических цепей переменного синусоидального тока
- •1. Параллельное соединение и
- •2. Последовательное соединение и
- •2.10 Мощность цепи переменного синусоидального тока
- •Баланс мощности в сложных
- •Метод контурных токов
- •Метод узловых потенциалов
- •Метод двух узлов
- •2. Несинусоидальные периодические токи.
- •3. Максимальные, средние и действующие значения
- •4. Расчет цепей при несинусоидальных эдс и токах.
- •5. Мощность цепи несинусоидального тока
- •3. Каскадное соединение четырехполюсников
- •2. Классический метод расчета переходных процессов
- •3. Переходные процессы в цепях синусоидального тока
- •4. Операторный метод расчета переходных процессов
- •5. Свойства (теоремы) преобразования Лапласа
- •1 Принцип построения трехфазной системы
- •2. Соединение звездой
- •3. Соединение треугольником
- •4. Мощность в трехфазных цепях
- •1. Основные определения
- •2. Свойства ферромагнитных материалов
- •3. Расчет магнитных цепей
- •4. Трансформатор
- •4.1. Устройство
- •4.2. Холостой ход
- •4.3. Режим нагрузки
- •4.4. Пример
Баланс мощности в сложных
ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Когда определены токи во всех ветвях, можно записать уравнение баланса мощности. Это позволит убедиться в правильности найденного решения. Если задача была решена с помощью метода узловых потенциалов, то можно воспользоваться следующей записью уравнения баланса мощности

Напряжение на ветви определяется разностью потенциалов ее концов
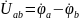 .
Было условлено считать, что положительные
направления отсчета напряжения на ветви
(на элементе цепи) совпадают с положительным
направлением тока. Итак, для электрической
цепи, изображенной на рисунке 2, должно
выполняться следующее равенство:
.
Было условлено считать, что положительные
направления отсчета напряжения на ветви
(на элементе цепи) совпадают с положительным
направлением тока. Итак, для электрической
цепи, изображенной на рисунке 2, должно
выполняться следующее равенство:
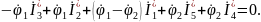
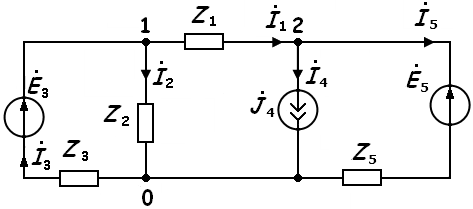
Теперь запишем уравнение баланса мощности для электрической цепи, изображенной на рисунке 1.
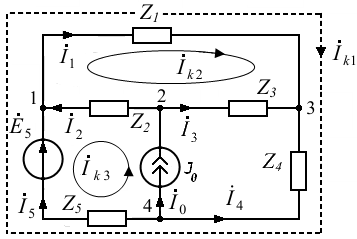
Токи в ветвях этой цепи были рассчитаны с помощью метод контурных токов. Напряжения на ветвях
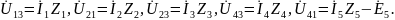
Напряжение
на ветви с источником тока
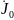 можно определить, как
можно определить, как

Следовательно, для этой электрической цепи должно выполняться равенство:
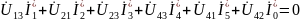
или
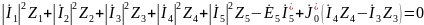
или

Если это равенство выполняется, значит, найденные значения токов в ветвях верны. Последняя запись уравнения баланса мощности говорит о том, что мощность, накопленная и расходуемая в пассивных элементах цепи, должна совпадать с мощностью, развиваемой всеми идеальными источниками энергии.
Билет 12
Метод контурных токов
Пусть
электрическая цепь содержит
 – ветвей,
– ветвей,
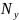 – узлов. Первый закон Кирхгофа позволяет
написать (
– узлов. Первый закон Кирхгофа позволяет
написать (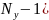 независимых уравнений. Второй закон
позволяет написать
независимых уравнений. Второй закон
позволяет написать
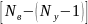 независимых уравнений. Их общее число
равно числу ветвей в цепи
.
независимых уравнений. Их общее число
равно числу ветвей в цепи
.
Метод контурных токов, позволяет сократить число уравнений, которые необходимо первоначально решить. Он заключается в том, что первоначально определяются вспомогательные – контурные токи. Искомые токи в каждой ветви являются алгебраической суммой контурных токов.
Решение задачи методом контурных токов основано на использовании второго закона Кирхгофа.
Число независимых уравнений при этом равно .
Предварительно в исследуемой цепи необходимо выбрать именно такое число контуров. Положительные направления искомых токов в ветвях выбираются произвольно, так же как произвольно выбирается направление контурных токов (направление обхода контуров). Рассмотрим схему на рисунке 1.
|
Уравнения будем писать для комплексных амплитуд, полагая, что в цепи действуют источники гармонических колебаний. В
задаче
|
Рисунок 1 |
Если
в цепи есть идеальные источники тока,
то следует контура выбирать так, чтобы
через ветви, содержащие такие источники,
проходил только один контур. При таком
выборе контуров
можно утверждать, что контурные токи
контуров, содержащих источники тока,
равны токам этих источников (с учетом
выбранного направления). В рассматриваемой
задаче
 .
.
Воспользуемся вторым законом Кирхгофа и запишем уравнения для
контуров 1 и 2 (которые выбраны и пронумерованы произвольно).
Для
контура 1:
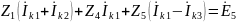 .
.
Для
контура 2:
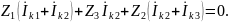
В
первом уравнении перед током
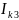 поставлен минус потому, что через элемент
поставлен минус потому, что через элемент
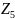 контурные токи
контурные токи
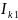 и
протекают
встречно, ток
направлен против выбранного направления
обхода контура. Преобразуем каждое из
уравнений:
и
протекают
встречно, ток
направлен против выбранного направления
обхода контура. Преобразуем каждое из
уравнений:
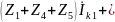
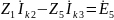 ,
,
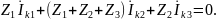
В
первом уравнении, написанном для контура
1,
сомножитель
 – это сумма комплексных сопротивлений
всех ветвей контура 1.
Множитель
– это сумма комплексных сопротивлений
всех ветвей контура 1.
Множитель
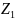 у
у
 – комплексное сопротивление ветви,
общей для контуров 1
и 2,
множитель
у
– это комплексное сопротивление ветви,
общей контуров 1
и 3.
В правой части уравнения стоит комплексная
амплитуда ЭДС источника, входящего в
контур 1.
– комплексное сопротивление ветви,
общей для контуров 1
и 2,
множитель
у
– это комплексное сопротивление ветви,
общей контуров 1
и 3.
В правой части уравнения стоит комплексная
амплитуда ЭДС источника, входящего в
контур 1.
Во
втором уравнении, составленном для
контура 2,
множителем контурного тока
этого контура является
 )
– комплексное сопротивление всех
ветвей, образующих контур 2,
а множители у контурных токов других
контуров – комплексные сопротивления
ветвей, общих для контура 2
и контура 1
или контура 3.
Правая часть уравнения равна 0,
во втором контуре источники ЭДС
отсутствуют.
)
– комплексное сопротивление всех
ветвей, образующих контур 2,
а множители у контурных токов других
контуров – комплексные сопротивления
ветвей, общих для контура 2
и контура 1
или контура 3.
Правая часть уравнения равна 0,
во втором контуре источники ЭДС
отсутствуют.
Согласно
методу контурных токов, для электрической
цепи, содержащей
 контуров, система уравнений в
формализованном виде будет выглядеть
следующим образом:
контуров, система уравнений в
формализованном виде будет выглядеть
следующим образом:
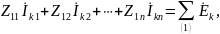
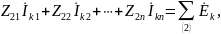
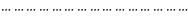

Здесь
 – комплексная
амплитуда контурного тока контура
– комплексная
амплитуда контурного тока контура
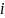 .
.
 – сумма
комплексных сопротивлений всех ветвей,
образующих контур
.
– сумма
комплексных сопротивлений всех ветвей,
образующих контур
.
 – алгебраическая
сумма комплексных сопротивлений ветвей,
общих для контура
и контура
– алгебраическая
сумма комплексных сопротивлений ветвей,
общих для контура
и контура
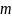 .
Знак перед такими слагаемыми положительный,
если направление контурных токов в
контурах
и
в рассматриваемой ветви совпадает. Если
между контурами
и
нет общей ветви, то
.
Знак перед такими слагаемыми положительный,
если направление контурных токов в
контурах
и
в рассматриваемой ветви совпадает. Если
между контурами
и
нет общей ветви, то
 .
.
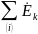 – алгебраическая
сумма комплексных амплитуд ЭДС источников
напряжения, включенных в контур
.
Слагаемые положительные, если направление
контурного тока
и направление источника ЭДС совпадают.
– алгебраическая
сумма комплексных амплитуд ЭДС источников
напряжения, включенных в контур
.
Слагаемые положительные, если направление
контурного тока
и направление источника ЭДС совпадают.
Результатом
решения системы являются комплексные
амплитуды контурных токов
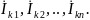 Токи в ветвях электрической цепи можно
определить алгебраическим сложением
контурных токов, протекающих через
рассматриваемые ветви. В нашем примере:
Токи в ветвях электрической цепи можно
определить алгебраическим сложением
контурных токов, протекающих через
рассматриваемые ветви. В нашем примере:

Проверить правильность записанных соотношений можно, применив первый закон Кирхгофа к токам в узлах. Например, для узла 1:

Билет 13

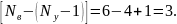 Следовательно, необходимо выбрать
три контура.
Следовательно, необходимо выбрать
три контура.