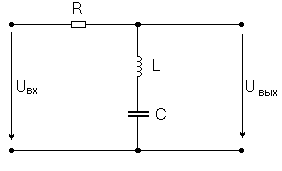
2. Последовательное соединение и

Рассмотрим схему на рисунке 3.

Рисунок 3 - Схема с последовательным соединением L и C

Определим комплексное (реактивное) сопротивление LC:

.

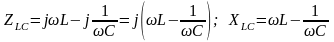Полное сопротивление

.

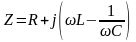Ток в цепи

.

Выходное напряжение

.

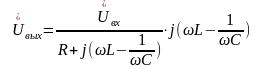Комплексный частотный коэффициент передачи

.

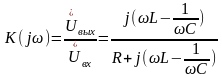Модуль частного коэффициента передачи:

;

;

.

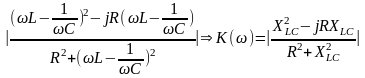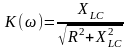На частотах резонанса и равно 0, т.е. .

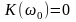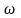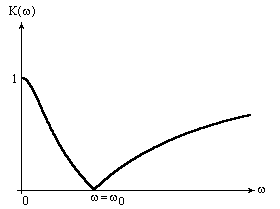
Если отлична от , то 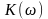находится в пределах от 1 до 0 (рисунок 4).

Рисунок 4 - Коэффициент передачи цепи с последовательным соединением L и C

Билет 11

2.10 Мощность цепи переменного синусоидального тока

Средняя потребляемая мощность для электрической цепи переменного синусоидального тока определяется выражением

.

Используя данное выражение, определим мощность, рассеиваемую на резисторе:

Обозначим:

где 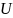и I - действующие значения напряжения и тока. Отсюда получим

.

С использованием комплексных величин средняя потребляемая мощность находится в соответствии с выражением

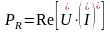
т.е. средняя потребляемая мощность находится как действительная часть от произведения комплексных величин: комплекс напряжения на сопряженный комплекс тока или комплекс тока на сопряженный комплекс напряжения.

Найдем среднюю мощность на конденсаторе и катушке индуктивности:

. .

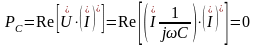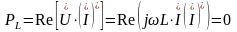В конденсаторе, так же, как и в катушке индуктивности, не рассеивается активная мощность.

При расчете мощности переменного тока используют следующее выражение:

,

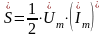где 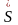- комплексная мощность.

Вещественная составляющая этого выражения равна средней мощности цепи. Мнимая составляющая называется реактивной мощностью цепи:

.

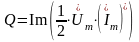Реактивная мощность характеризует наличие в цепи реактивных элементов – катушек индуктивности или конденсаторов. Если цепь содержит только резисторы, то между токами и напряжениями на любых участках этой цепи фазовые сдвиги равны нулю и . Если цепь содержит только конденсаторы или только катушки индуктивности, то значения 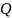максимальны.

Реактивная мощность измеряется в «варах» (Вар).

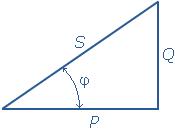
	Максимально допустимая реактивная мощность указывается в технических данных на конденсаторы и на некоторые катушки индуктивности. Полную комплексную мощность можно представить на комплексной плоскости в виде треугольника мощностей (рисунок 5).
Рисунок 5 – Треугольник мощностей

Полная мощность измеряется в вольт-амперах (ВА). Полная мощность понимается как максимальное значение модуля комплексной мощности, которую может потреблять цепь. Полную мощность указывают в технических данных на электрогенераторы переменного тока.

В электрической цепи есть две разновидности элементов: активные, которые генерируют электрическую энергию (источники тока и источники напряжения), и пассивные, которые потребляют энергию. Катушка индуктивности и конденсатор могут часть периода отдавать энергию во внешнюю цепь, но генераторами не являются, так как отдают энергию, накопленную за предыдущую часть периода.

В сложных целях с несколькими источниками напряжения и тока и с большим количеством пассивных элементов действует закон сохранения энергии. Уравнение баланса полных комплексных мощностей записывается следующим образом:

,

где – полная комплексная мощность источника, а 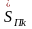– полная комплексная мощность, потребляемая элементом.

Уравнение баланса мощностей можно разбить на два уравнения – для активных и реактивных мощностей:

, .

Рассмотрим электрическую цепь (рисунок 6).

Рисунок 6 - Схема цепи

Комплексное сопротивление цепи и комплексный ток цепи равны:

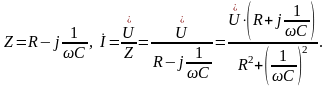
Комплексная и активная мощности цепи:

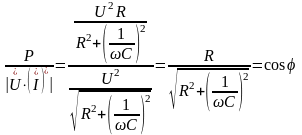Определим полную мощность:

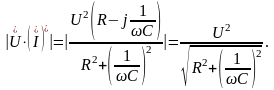
Найдем отношение:

.

Данное отношени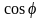е называется коэффициентом мощности. Для уменьшения реактивных токов стремятся коэффициент мощности сделать как можно больше.