- •8 Теорема об эквивалентном генераторе
- •1.9 Преобразование реального источника напряжения в реальный источник тока
- •1.10 Преобразование треугольника сопротивлений в эквивалентную звезду
- •1.11 Преобразование звезды сопротивлений в эквивалентный треугольник
- •2.2 Разряд и заряд конденсатора через резистор
- •2.3 Конденсатор в цепи переменного синусоидального тока
- •2.5 Переходные процессы в цепях с катушкой индуктивности
- •2.6 Катушка индуктивности в цепи переменного
- •2.7 Использование комплексных чисел при расчете электрических цепей переменного синусоидального тока
- •1. Параллельное соединение и
- •2. Последовательное соединение и
- •2.10 Мощность цепи переменного синусоидального тока
- •Баланс мощности в сложных
- •Метод контурных токов
- •Метод узловых потенциалов
- •Метод двух узлов
- •2. Несинусоидальные периодические токи.
- •3. Максимальные, средние и действующие значения
- •4. Расчет цепей при несинусоидальных эдс и токах.
- •5. Мощность цепи несинусоидального тока
- •3. Каскадное соединение четырехполюсников
- •2. Классический метод расчета переходных процессов
- •3. Переходные процессы в цепях синусоидального тока
- •4. Операторный метод расчета переходных процессов
- •5. Свойства (теоремы) преобразования Лапласа
- •1 Принцип построения трехфазной системы
- •2. Соединение звездой
- •3. Соединение треугольником
- •4. Мощность в трехфазных цепях
- •1. Основные определения
- •2. Свойства ферромагнитных материалов
- •3. Расчет магнитных цепей
- •4. Трансформатор
- •4.1. Устройство
- •4.2. Холостой ход
- •4.3. Режим нагрузки
- •4.4. Пример
2.6 Катушка индуктивности в цепи переменного
синусоидального тока
Пусть через катушку индуктивности протекает переменный синусоидальный ток
 .
.
Определим изменение напряжения на катушке индуктивности

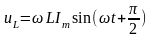 .
.
Из последнего выражения следует:
1)
амплитуды напряжения и тока в катушке
индуктивности связаны соотношением:
 ,
где
,
где
 - индуктивное сопротивление или
сопротивление катушки индуктивности
в цепи переменного синусоидального
тока;
- индуктивное сопротивление или
сопротивление катушки индуктивности
в цепи переменного синусоидального
тока;
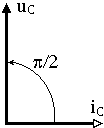
2) напряжение на катушке индуктивности опережает ток в ней на угол (рисунок 2.14).
|
Рисунок 2.14 |
Билет 8
2.7 Использование комплексных чисел при расчете электрических цепей переменного синусоидального тока
Напряжение
согласно рассматриваемому методу
представляется следующим образом:
 ,
,
где
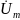 – комплексное изображение синусоидального
напряжения (комплекс напряжения).
– комплексное изображение синусоидального
напряжения (комплекс напряжения).
Ток представляется следующим образом:
 ,
,
где
 – комплексное изображение синусоидального
тока (комплекс тока).
– комплексное изображение синусоидального
тока (комплекс тока).
Для обратного перехода от комплекса напряжения или тока необходимо:
1)
умножить комплекс на
 ;
;
2) взять мнимую часть от полученного комплексного числа.
Метод расчета с помощью комплексных чисел заключается в замене реальных токов и напряжений их комплексными изображениями, расчете электрической цепи и последующем переходе от рассчитанных комплексов к мгновенным значениям токов и напряжений (к оригиналам).
Рассмотрим изображение производной в соответствии с комплексным методом:


Дифференцирование
синусоидальной функции соответствует
умножению изображения этой синусоидальной
функции на комплексное число
 .
.
Рассмотрим изображение интеграла в соответствии с комплексным методом:

 .
.
Интегрирование синусоидальной функции соответствует делению изображения на .
Найдем изображение тока через конденсатор:

где
 -
комплексное сопротивление конденсатора.
-
комплексное сопротивление конденсатора.
Изображение напряжения на катушке индуктивности:

где
 - комплексное сопротивление катушки
индуктивности.
- комплексное сопротивление катушки
индуктивности.
|
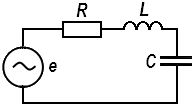
Рассмотрим
электрическую цепь, изображенную на
рисунке 2.15.Составим по второму закону
Кирхгофа уравнение для мгновенных
значений напряжения и тока в данной
цепи:
|
Рисунок 2.15 |
Используя комплексные изображения, получим
 .
.
Находим комплекс тока:
 ,
,
где
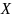 – реактивное сопротивление электрической
цепи;
– реактивное сопротивление электрической
цепи;
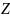 – полное
комплексное сопротивление электрической
цепи.
– полное
комплексное сопротивление электрической
цепи.
Выражение

называется законом Ома в комплексной форме.
Таким образом, используя метод комплексных чисел, можно применять закон Ома для электрических схем переменного синусоидального тока. То же касается и законов Кирхгофа. После расчетов по этим законам определяют комплексы мнимых величин. В конце расчета осуществляется переход от комплексов к мгновенным значениям (оригиналам).
Переход
осуществляется по схеме:
 .
.
Билет 9
1. Параллельное соединение и
Рассмотрим схему
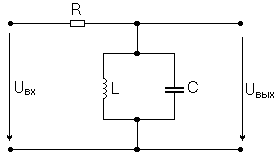
Рисунок 1 - Схема с параллельным соединением L и C
Определим реактивное сопротивление LC:
 ,
,
 .
.
Определим комплекс выходного напряжения электрической цепи:
 .
.
Коэффициент передачи будет равен
 .
.
Модуль частотного коэффициента передачи:

 .
.
 .
.
Если
 ,
то
,
то
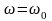 ,
,
 .
.
Если
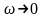 ,
то
,
то
 ,
,
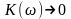 .
.
Если
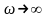 ,
то
,
,
то
,
График
 представлен на рисунке 2.
представлен на рисунке 2.
|
Рисунок 2 - Коэффициент передачи цепи с параллельным соединением L и C |
Электрическая
цепь обладает свойством избирательности,
т.е. через эту цепь наилучшим образом
проходят электрические сигналы с
частотой
 .
Частота
называется резонансной частотой
.
Частота
называется резонансной частотой
Билет 10

 .
.