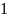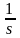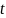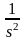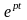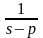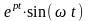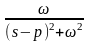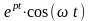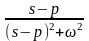4. Операторный метод расчета переходных процессов

Идея операторного метода заключается в том, что расчет переходного процесса переносится из области функций действительной переменной (времени t) в область функций комплексного переменного , в которой дифференциальные уравнения преобразуются в алгебраические уравнения. Такое преобразование называется прямым. Полученное решение обратным преобразованием переносится в область действительного переменного.

Для прямого преобразования функций времени применяется преобразование Лапласа

,

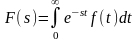что сокращенно записывается так:

,

где 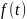– функция времени, называемая оригиналом, определена при , интегрируема в интервале времени 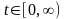и равна нулю при ;

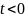– функция комплексного переменного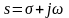 , называемая лапласовым изображением.

Примем, что начало переходного процесса в цепи соответствует моменту времени .

В таблице 1 приведены примеры изображения простых функций.

Таблица 1 – Изображения функций по Лапласу

Оригинал	Изображение

Билет 25

5. Свойства (теоремы) преобразования Лапласа

Теорема о сложении или линейность преобразования:

.

Теорема об интегрировании:

.

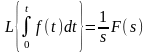Теорема о дифференцировании:

.

Теорема запаздывания:

.

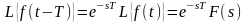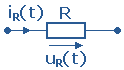
Преобразование Лапласа позволяет получить для резистивного, индуктивного и емкостного элементов соотношения между напряжением и током в операторной форме (рисунке 2).

Рисунок 2 - Операторные схемы замещения элементов

При расчете переходного процесса операторным методом можно выделить несколько логически самостоятельных этапов:

1) представить исходные данные о параметрах всех элементов схемы цепи в операторной форме. Это означает, что, во-первых, ЭДС источников напряжения и токи источников тока, заданные мгновенными значениями и , следует представить соответствующими изображениями и и, во-вторых, пассивные элементы – схемами замещения по рисунку 2;

2) для полученной схемы замещения в операторной форме составить и решить полную систему независимых уравнений по первому и второму законам Кирхгофа в операторной форме, т. е. найти изображение искомой величины, например, ток ;

3) обратным преобразованием нужно найти оригинал , например, ток .

Пример. Рассчитаем ток в катушке индуктивности в цепи (рисунок 3), содержащей ЭДС , и при нулевых начальных условиях.

Рисунок 3

Для выбранных положительных направлений токов составим одно уравнение по первому закону Кирхгофа для узла «а»:

и два уравнения по второму закону Кирхгофа:

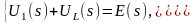
или

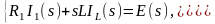
Решая систему из 3-х уравнений, получаем

.

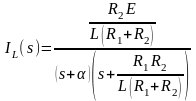Воспользуемся таблицей преобразований, получим

.

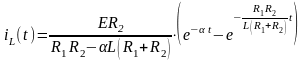Билет 26