Оглавление

«Функциональный Анализ» by OZ

1. Какое множество называется линейным пространством?

Множество L называется линейным (векторным) пространством, если:

1. Дано правило, указывающее, как для любых двух элементов a, b из L найти в L некоторый элемент, называемый их суммой и обозначаемый символом a+b:

;

2. Дано правило, указывающее, как для любого вещественного (или комплексного) числа α и любого элемента a из L найти в L новый элемент, называемый произведением α на a и обозначаемый αa или aα.

3. Определено понятие равенства элементов в L, обозначаемое знаком “=”.

4. Для сложения и умножения на число существует 8 условий:

• Сложение коммутативно: a + b = b + a;

• Сложение ассоциативно: (a + b) + с = a + (b + c);

• Умножение ассоциативно: α(βa) = (αβ)a;

• Умножение дистрибутивно по отношению к сложению элементов из L: α(a + b) = αa + αβ;

• Умножение дистрибутивно по отношению к сложению чисел: (α + β)a = αa + βa;

• Существует такой элемент 0, называемый нулевым, что a+0=a для любого элемента а;

• Для любого элемента а: a*1=a;

• Для любого элемента а существует такой элемент –а, называемый противоположным элементу а, что a+(-a)=0.

2. Какие условия налагаются на операции сложения и умножения на число в линейном пространстве?

Для сложения и умножения на число существует 8 условий:

1. Сложение коммутативно: a + b = b + a;

2. Сложение ассоциативно: (a + b) + с = a + (b + c);

3. Умножение ассоциативно: α(βa) = (αβ)a;

4. Умножение дистрибутивно по отношению к сложению элементов из L: α(a + b) = αa + αβ;

5. Умножение дистрибутивно по отношению к сложению чисел: (α + β)a = αa + βa;

6. Существует такой элемент 0, называемый нулевым, что a+0=a для любого элемента а;

7. Для любого элемента а: a*1=a;

8. Для любого элемента а существует такой элемент –а, называемый противоположным элементу а, что a+(-a)=0.

3. В каком случае линейное пространство называется вещественным, а в каком комплексным?

Если произведение αa определено только для вещественных чисел, то линейное пространство L называется вещественным, если же произведение αa определено для любого комплексного числа α, то линейное пространство L называется комплексным. Элементы линейного пространства называются векторами (или точками) и обозначаются буквами a, b, x, y.

4. Какими свойствами характеризуется линейное пространство?

Свойства линейного пространства:

1. В каждом линейном пространстве существует единственный нулевой вектор.

2. В каждом линейном пространстве для каждого вектора существует единственный противоположный вектор.

3. В любом линейном пространстве для всякого вектора имеет место равенство 0*а=О; в левой части равенства символ 0 означает число нуль, а в правой – нулевой вектор О.

4. Произведение любого числа a на нулевой вектор равно нулевому вектору, т.е. a*0=0

5. Для каждого элемента а противоположный элемент равен произведению этого элемента на число -1, т.е. –а = (-1)*а.

5. Приведите примеры линейных пространств.

6. Что такое линейная комбинация векторов в линейном пространстве?

Линейная комбинация векторов а₁, а₂, …, a_n – сумма произведений этих элементов на произвольные вещественные числа C₁, C₂, …,C_n, т.е. вектор C₁а₁ + C₂а₂ + …+C_nа_n, где C₁, C₂, …,C_n – коэффициенты этой линейной комбинации.

7. В каком случае вектора линейного пространства называются линейно зависимыми?

Векторы а₁, а₂, …, a_n называются линейно зависимыми, если существует n чисел из которых не все равны 0, такие что выполняется равенство 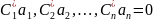. Если же равенство возможно только в единственном случае, когда 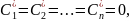то векторы а₁, а₂, …, a_n называются линейно независимыми.

Теорема и доказательство на всякий пожарный, для ответа они НЕ нужны, как и пример, добавлены

из соображений: «А вдруг?»