17 Производственная функция.

Для орг-ции произв-ного процесса предприниматель должен иметь необходимые ф-ры произ-ва, кот. д. сущ-ть в опред. кол-ве и в опред. Соотношении. Зависимость максимального объема произведенного продукта от затрат используемых факторов произв-ва наз. Произв-ной ф-цией

Где Q – максимальный объем продукции, кот. возможен при заданной технологии и опред ф-рах произв-ва. К – затраты капитала, L – затраты труда, М – затраты сырья и мат-ов.

Для укрупненного анализа и прогнозирования исп-ся произв-ная ф-ция Кобба-Дугласа:

Где Q – максимальный объем продукции, кот. возможен при заданных ф-рах произв-ва. К – затраты капитала, L – затраты труда, М – затраты сырья и мат-ов, α, β, γ – коэф-ты эласатичности объема произв-ва соот-но по капиталу, труду и мат-лам.

α+β+γ=1

Производственная функция обладает рядом общих св-в: 1- ф-ры произв-ва явл. взаимодоп-данный процесс произв-ва возможен только при наборе опред. ф-ров; 2-сущ. опред. взаимозаменяемость ф-ров,т.е. в процессе произв-ва один фактор м.б. заменен в опред. пропорции др. Это не предполаг. полного искл-я какого-то ф-ра. Разные комбинации ф-ров дают. разн. объемы производственной продукции. Сущ. опред. предел роста объема произ-ва при увеличении одного ф-ра, если остальные ф-ры остаются постоянными – з-н убывающей произв-ти или убыв. отдачи. этот закон характеризует произв-ую фун-ию с одним переменным ф-ром. Q=f(x;y) y – постоян. Ф-р; х – перемен. Ф-р.

Сущ. понятие общего, среднего, предельного продукта. Общ. продукт – (ТР) общее кол-во произведенного продукта, кот. изменяется по мере увел. исп-ия перемен ф-ра. Средний продукт (АР) – отношение общего продукта к кол-ву переменного фактора используемогов произ-ве АР=ТР/х. Предельн. продукт (МР)-кол-во доп. продукта, получен. при исп-ии дополнительной единицы перемен. ресурса, т.е. МР=∆ТР/∆х. М. сущ положение, когда переменными станов-ся 2 фактора произв-ва, кот. при определ. сочетании дают один и тот же объем произ. продукта. Для примера возьмем затраты труда и капитала припроиз-ве джинс. Затраты труда-Х, а капитала-Y. При отпред-ой комбинации этих ф-ров м.б. произведено 200 джинс, Q=200. М. увеличить величину применяемого капитала и уменьшить применение живого труда. При этом общ объем произ-ва останется на прежнем уровне. Эта зав-ть предств графич с исп-ем изокванты.

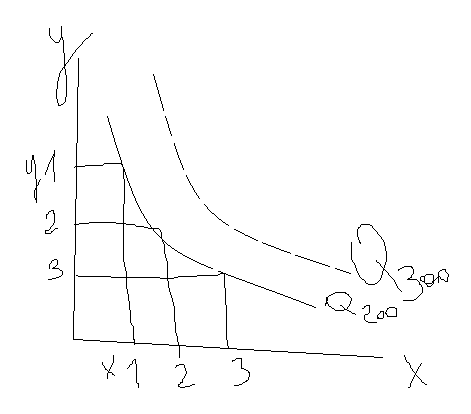
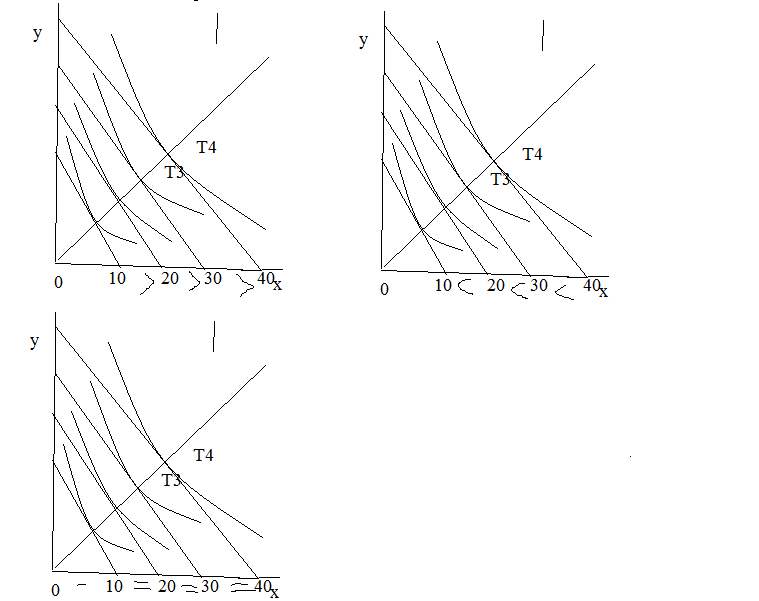
Изокванта (кривая равного) продукта отражает все возмож. комбинации 2х ф-ров, кот. м.б. исп для произв-ва опред. объема продукта. Исп перемен. ф-ров в больших объемах м. увеличить выпуск готовой продукции. Изокванта,отражающая произ-во большого объема продукта, будет располож правее и выше первой изокванты.Кол-во исп-х факторов х,y м. постоянно меняться , что соответ. скажется на max выупске продукта. М. утв-ть, что сущ. множество изоквант, кот. показ. разные объемы выпуска продукции, они образуют карту изоквант.

Изокванты для процесса произв-ва означают тоже, что и кривые безразличия для процесса потребления, они обл. аналогичн. св-вами, имеют «-» наклон, выпуклы вниз, непересек. др. с др., однако в отличие от кривых безразличия , где суммар. удовлетворение потребителя измерить нельзя, изокванты показ. реальный уровень произв-ва. Возникает вопрос на сколько нужно увел. объем капитала, чтобы умен. на 1го человека применения живого труда. Для этого необходимо рассм-ть крутизну наклона изованты, кот. харак-ся предельной нормой технологического замещения. В зоне технического замещения изокванты низшего порядка не пересекаются с изоквантами более высокого уровня. Для наглядности представим пересечение изоквант:

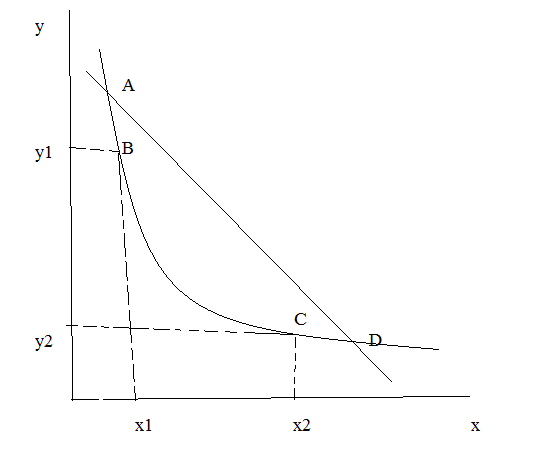
Предположим, что изокванта 1 перес. 2 в точках А и Д, это озаначает, что для произв-ва меньшего кол-ва продукции требуется столько же ресурсов, сколько было бы достаточно было для произв-ва большего кол-ва , такая 17произв-ая комбинация неэфф-на. Для рационального произ-ва проблема выбора оптимального сочетания ресурсов м.б. поставлена лишь в пределах зоны техн. замещения (субституции), т.е. в пределах кривой ВС, именно этот отрезок рассм. дальше. Увеличение затрат фактора х(труда) компенсируется уменьшением затрат фактора у(капитала). Угловой коэффициент изокванты показыв. как происх. техн. замещение капитала трудом. Абсолютное значение этого коэф-та харак. предельную норму техн. замещения (МRTS). Она аналог. предельной норме замещения MPS в теории замещения потреб-ля. Пред. норма техн. замещения измеряется соотн-ем изменения ф-ра у изменением ф-ра х , поскольку замена ф-ров происходит в обратном отношении, то матем. изображение показателя MRTSху берется со знаком «-»: MRTSху= -∆у/∆х, изобразим график:

MRTSху= tg α. Можно отметить, что в верх. части изокванты угол будет достаточно велик, это говорит о том что, для изменения ф-ра х на 1 ед. требуется значит. изменение ф-ра у => в этой части кривой значение MRTSху б. велико. По мере движения вниз по изокванте значение предельной нормы тенх. замещения б. убывать. Умен-е MRTS одного ф-ра др. свидетельствует о том, что эфф-ть исп-я любого ресурса ограничено. По мере замены капитала трудом отдача последнего снижается, аналог. ситуация когда труд замен. капиталом. Анализ произв-ва с помощ. изоквант имеет недостатки, т.к. при этом использ. только натур. показатели затрат ресурса и выпуска продукции. Максимизировать выпуск при данных издержках или затратах позволяет прямая равных издержек или износа. Если Р₁ цена фактора произв-ва х, Р₂-цена фактора у, то располагая опред. бюджетом С, производитель м. купить n ед. факора х, и m ед. фактора у: С=Р₁n+Р₂m или m= -(P_1*n/P₂)+C/Р_2. С увелич.средст на приобретение перемен ф-ров, изокосты б. сдвигаться вправо и вверх. Графически изокосты выгляд. также как бюдж. линия потребителя. При неизменных ценах изокосты – это прямые параллел. линии с «-» углом наклона. Уравнение прямой издержек предст. комбинацию ресу-ов, исп-е кот. ведет к одинаковым затратам, израсх. на произв-во. Касание изокосты с изоквантой опред. положение равнов. произ-ля, поскольку позволяет достичь max объема произв-ва при имеющ-ся огран. средствах, учитывая что в точке Т изокванта и изокоста имеют один наклон, что наклон изокванты измеряется предел. нормой техн. замещения. М написать условие равновесия: MRTSху= -∆у/∆х= P_y/P_x= МP₂/МP₁= r/w, где r – плата за час работы оборудования; w –ставка за час работника. Точка равновесия производителя будет достигнута тогда, когда отклонение предел. продукта капитала к цене и ед. капитала б = соотношению предел. продукта труда к цене ед. труда. Предположим, что цены ресурсов остаются неизм-ми, тогда как бюджет произ-ля постоянно растет, соед-в точки касания изоквант с изокостами => линию OS – «путь развития», аналог. линии «уровня жизни» в теории поведения потребителя.

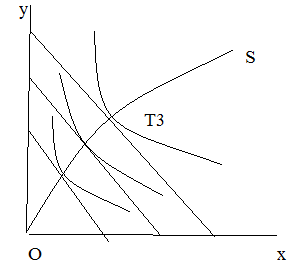
Эти линии показыв. изменение соотношения м/у факторами в процессе расширения произв-ва. Форма кривой «путь развития» зав-т от формы изокванты, цен на ресурсы. Линия «путь развития» м.б. прямой или кривой исходящей из начала координат. Если расстояние м/у изоквантами уменш-ся, это говорит о том, что сущ возраст-ая экономия от масштаба, т.е. увеличения выпуска достигается при относит-ой экономики ресурсов. Если расстояние м/у изоквантами увелич-убывающ экономия от масштаба. Когда увелич-ие произ-ва пропор-цно увелич ресурсов-постоян экономия от масштаба. В случае возраст. экономии от масштаба, фирме необх. наращивать объем произв-ва, то это приводит к относит. экономии имеющихся ресурсов.