
- •Учебно-методический комплекс по дисциплине математика
- •270802 Строительство и эксплуатация зданий и сооружений
- •Для студентов очной формы обучения Альметьевск, 2012
- •Содержание
- •Уважаемый студент!
- •Раздел 1 алгебра
- •Тема 1.1 Элементы вычислительной математики
- •1.1.2. Приближенные значения величин
- •Тема 1.2. Корень. Степень
- •1.2.1. Корень n-ой степени.
- •1.2.2. Степень с рациональным показателем
- •Тема 1.3. Логарифмы
- •Понятие о логарифме числа.
- •Тема 1.4. Тригонометрия
- •Радианная и градусная меры углов
- •1.4.2. Формулы двойного аргумента
- •Тема 1.5. Комплексные числа
- •1.5.1. Понятие о мнимых и комплексных числах.
- •1.5.2. Формы записи комплексных чисел
- •Раздел 2. Функции и графики
- •Тема 2.1. Построение графиков функций
- •2.1.1. Графики показательных функций
- •2.1.2. Графики логарифмических функций
- •Раздел 3. Уравнения и неравенства
- •Тема 3.1. Рациональные уравнения и неравенства
- •3.1.1. Квадратные уравнения и неравенства. Метод интервалов
- •3.1.2. Определители второго порядка
- •3.1.3. Решение систем двух уравнений методом Крамера
- •3.1.4. Метод Гаусса
- •3.1.5. Решение текстовых задач на составление уравнений
- •Тема 3.2. Показательные уравнения и неравенства
- •3.2.1. Простейшие показательные уравнения и неравенства
- •3.2.2. Применение свойств степеней.
- •3.2.3. Показательные уравнения и неравенства, сводящиеся к квадратным
- •Тема 3.3. Логарифмические уравнения и неравенства
- •3.3.1. Простейшие логарифмические уравнения и неравенства
- •3.3.3. Применение свойств логарифмов
- •3.3.4. Логарифмические уравнения и неравенства, сводящиеся к квадратным
- •3.3.5. Системы логарифмических уравнений
- •Тема 3.4. Тригонометрические уравнения и неравенства
- •3.4.1. Обратные тригонометрические функции.
- •3.4.4. Решение тригонометрических уравнений разложением на множители
- •3.4.5. Решение тригонометрических уравнений разными способами
- •3.4.6. Тригонометрические неравенства.
- •Раздел 4. Начала математического анализа
- •Тема 4.1. Пределы функции
- •4.1.1. Последовательности. Предел функции
- •4.1.2. I и II замечательные пределы
- •Тема 4.2. Производная
- •4.2.1. Приращение функции. Производная
- •4.2.2. Правила дифференцирования
- •Тема 4.3. Приложения производной
- •4.3.1. Физический смысл производной. Мгновенная скорость. Ускорение
- •4.3.2. Геометрический смысл производной. Уравнение касательной
- •4.3.3. Возрастание и убывание функции. Точки экстремума
- •4.3.4. Выпуклость графика функции. Точка перегиба
- •4.3.5. Асимптоты
- •Тема4.4. Неопределенный интеграл
- •4.4.1. Первообразная функция
- •4.4.2. Неопределенный интеграл
- •Тема4.5. Определенный интеграл
- •4.5.1. Формула Ньютона-Лейбница
- •4.5.2. Метод замены переменной
- •Тема4.6. Приложения определенного интеграла
- •4.6.1. Площадь криволинейной трапеции
- •4.6.2. Вычисление пути, пройденного телом
- •Тема 4.7. Дифференциальные уравнения
- •4.7.1. Основные понятия дифференциального уравнения
- •4.7.2. Линейные однородные дифференциальные уравнения первого порядка
- •4.7.3 Линейные неоднородные дифференциальные уравнения первого порядка
- •Раздел 5. Комбинаторика, статистика и теория вероятностей
- •Тема 5.1. Элементы комбинаторики и теория вероятностей
- •5.1.1. Перестановки и факториалы. Правило умножения
- •5.1.2. Сочетание и размещение
- •5.1.3. Вероятности случайных событий
- •5.1.4. Сложение и умножение вероятностей случайных событий
- •Тема 5.2. Математическая статистика
- •5.2.1. Задачи математической статистики
- •5.2.2. Центральные тенденции: среднее значение, мода, медиана
- •Раздел 6. Геометрия
- •Тема 6.1. Элементы векторной алгебры и аналитической геометрии
- •6.1.1. Векторы. Действия над векторами.
- •6.1.2. Скалярное произведение векторов
- •6.1.3. Векторное произведение векторов
- •6.1.4. Прямая линия на плоскости. Уравнения прямых
- •6.1.5. Линии второго порядка на плоскости
- •Тема 6.2. Прямая и плоскость в пространстве
- •6.2.1. Аксиомы стереометрии
- •6.2.2. Взаимное расположение прямых и плоскостей в пространстве
- •Тема 6.3. Многогранники
- •6.3.1. Решение планиметрических задач
- •6.3.2. Призма.
- •6.3.3. Параллелепипед
- •Основные элементы
- •6.3.4. Пирамида.
- •6.3.5. Усеченная пирамида
- •6.3.6. Правильные многогранники
- •Тема 6.4. Тела вращения
- •6.4.1. Цилиндр
- •6.4.2. Площади поверхностей и объем цилиндра
- •6.4.3. Конус
- •6.4.4. Площади поверхностей и объем конуса
- •6.4.5. Усеченный конус
- •6.4.6. Шар и сфера
- •Контроль и оценка результатов освоения дисциплины Текущий контроль
- •Итоговый контроль Вопросы к дифференцированному зачету
- •Вопросы к экзамену
- •Глоссарий Абсолютная погрешность - разность между приближенным числом и его точным значением (из большего числа вычитается меньшее).
- •Информационное обеспечение дисциплины Основные источники
- •Дополнительные источники
Тема 3.2. Показательные уравнения и неравенства
3.2.1. Простейшие показательные уравнения и неравенства
Основные понятия и термины: показательные уравнения, показательные неравенства
План изучения темы:
1. Устный опрос
2. Теоретическая часть
3. Практическая работа 25
4. Практическая работа 26
Краткое изложение теоретических вопросов:
Пример 1. 1000x=100
Решение:
Представим левую и правую часть уравнения в виде степени, имеющую одинаковые основания: 103x=102
Теперь, когда основания одинаковые, нужно приравнять показатели степеней.
3x=2 x=2/3
Ответ: 2/3 .
Пример 2. 3х2-х-2=81
Решение:
3х2-х-2=34
Приравниваем показатели:
х2-х-2=4
х2-х-6=0
Получили квадратное уравнение:
D=1+24=25, D>0, следовательно, уравнение имеет два действительных корня
х1=(1+5)/2=3
х2=(1-5)/2=-2
Ответ: х=3 и х=-2
Рассмотрим
решение показательных неравенств вида
![]() ,
где b – некоторое рациональное число.
Если
a>1,
то показательная функция
,
где b – некоторое рациональное число.
Если
a>1,
то показательная функция
![]() монотонно
возрастает и определена при всех х. Для
возрастающей функции большему значению
функции соответствует большее значение
аргумента. Тогда неравенство
монотонно
возрастает и определена при всех х. Для
возрастающей функции большему значению
функции соответствует большее значение
аргумента. Тогда неравенство![]() равносильно
неравенству
равносильно
неравенству
![]() .
Если
0<a<1,
то показательная функция
.
Если
0<a<1,
то показательная функция
![]() монотонно
убывает и определена при всех х. Для
убывающей функции большему значению
функции соответствует меньшее значение
аргумента. Тогда неравенство
монотонно
убывает и определена при всех х. Для
убывающей функции большему значению
функции соответствует меньшее значение
аргумента. Тогда неравенство![]() равносильно
неравенству
равносильно
неравенству
![]()
Пример
3.
Решим неравенство
![]()
Запишем
неравенство в виде
![]() .
Т. к.
.
Т. к.
![]() ,
то показательная функция
,
то показательная функция
![]() возрастает.
Поэтому данное неравенство равносильно
неравенству
возрастает.
Поэтому данное неравенство равносильно
неравенству
![]() .
Ответ:
.
Ответ:
![]() .
.
Пример
4.
Решим неравенство
 .
.
Запишем
неравенство в виде
 .
.
Показательная
функция
 убывает.
Поэтому данное неравенство равносильно
неравенству х
< - 3
убывает.
Поэтому данное неравенство равносильно
неравенству х
< - 3
Ответ:
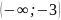 .
.
Практические занятия
1. Решение простейших показательных уравнений
2. Решение простейших показательных неравенств
Задания для самостоятельного выполнения
1 |
271-х
=
|
82
+ 3х = |
|
2 |
2163х
+ 1 =
|
|
|
3 |
13х = 1
|
|
|
Форма контроля самостоятельной работы:
Устный опрос
Проверка тетрадей
Вопросы для самоконтроля по теме:
1. Какие уравнения называются показательными?
2. Какие неравенства называются показательными?
3.2.2. Применение свойств степеней.
Основные понятия и термины: равносильность уравнений, равносильность неравенств
План изучения темы:
1. Устный опрос
2. Теоретическая часть
3. Решение показательных уравнений
4. Решение показательных неравенств
Краткое изложение теоретических вопросов:
При решении показательных уравнений главные правила - действия со степенями.
Пример 1. 4х+1+4х=320
Решение:
В таких случаях выносится основание с наименьшим показателем. В данном уравнении наименьшим показателем является х. Вынесем 4х за скобки:
4х(4+1)=320 4х ∙5=320
Представим 320 в виде 5∙43, тогда: 4х∙5=5∙43
Поделим левую и правую часть уравнения на 5: 4х=43
Приравняем показатели: х=3
Ответ: 3
Практические занятия не предусмотрены
Задания для самостоятельного выполнения
1 |
2х + 2х + 1 = 6
|
7х + 2 - 14•7х = 5 |
10•5х -1 + 5х + 1 = 7
|
2 |
5х + 1 + 5х + 5х – 1 = 31
|
2х + 4 – 2х = 120 |
3х + 2 + 3х + 1 + 3х = 39 |
3 |
2х
+ 2х + 1
|
2х + 3 + 2х + 1 - 7•2х = 48
|
5х
+ 5 х
+ 1
|
Форма контроля самостоятельной работы:
Устный опрос
Проверка тетрадей
Вопросы для самоконтроля по теме:
1. Основные методы решения показательных уравнений и неравенств







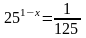

 6
6 30
30