Раздел 3. Уравнения и неравенства

Тема 3.1. Рациональные уравнения и неравенства

3.1.1. Квадратные уравнения и неравенства. Метод интервалов

Основные понятия и термины: уравнение, неравенство

План изучения темы:

1. Устный опрос

2. Теоретическая часть

3. Решение квадратных уравнений разными способами

4. Решение квадратных неравенств методом интервалов

Краткое изложение теоретических вопросов:

Уравнение вида ax ²  +  bx  +  c  = 0, где x − переменная, a ,  b  и  c − некоторые действительные числа, называется квадратным уравнением. Коэффициенты a,b,c имеют соответственно названия: а - старший коэффициент (коэффициент при x² ), b- второй коэффициент (коэффициент при x),   c - свободный член.

Корнем квадратного уравнения называется такое значение переменной, при подстановке которого квадратный трехчлен ax ²  +  bx  +  c   обращается в ноль.

Если старший коэффициент a=1 , то квадратное уравнение является приведенным, если же a≠1, то неприведенным.

Квадратное уравнение называется полным, если оно содержит все три слагаемых (то есть коэффициенты и не равны нулю).

Квадратное уравнение называется неполным, если оно содержит не все три слагаемых (то есть коэффициент b=0 или c=0 или b=0 и c=0).

При решении квадратного уравнения ax ²  +  bx  +  c  = 0 необходимо придерживаться следующей схемы:

1)      Найти дискриминант по формуле: D  =  b ²  – 4 ac

2)      Найти корни квадратного уравнения, опираясь на следующие рассуждения:

- Если D  < 0, то квадратное уравнение имеет 2 корня (комплексные числа);

-Если D  > 0, то квадратное уравнение имеет два действительных корня, которые находятся по формулам:

-Если D  = 0, то корни совпадают и равны:

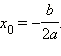
Теорема Виета. Если приведенное квадратное уравнение x² + px + q = 0 имеет действительные корни, то их сумма равна - p, а произведение равно q, то есть x₁ + x₂ = - p , x₁ x₂ = q

(сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену).

Практические занятия не предусмотрены

Задания для самостоятельного выполнения

Конспекты на темы:

1. Решение линейных уравнений с одной переменной

2. Решение линейных неравенств с одной переменной

3. Квадратные уравнения

Форма контроля самостоятельной работы:

• Устный опрос

• Проверка тетрадей

Вопросы для самоконтроля по теме:

1. Какое уравнение называется квадратным уравнением общего вида и какое приведенным квадратным уравнением?

2. Какое выражение называется дискриминантом квадратного уравнения общего вида?

3. Какие уравнения называются неполными квадратными?

4. По какой формуле квадратный трехчлен раскладывается на линейные множители?

3.1.2. Определители второго порядка

Основные понятия и термины: определители, главная диагональ, побочная диагональ

План изучения темы:

1. Устный опрос

2. Теоретическая часть

3. Практическая работа 21

Краткое изложение теоретических вопросов:

Определителем второго порядка называется число

.

Первый индекс указывает номер строки, а второй — номер столбца, в которой стоит данное число. Например, а₁₂ означает число, стоящее в первой строке и втором столбце; а₂₁ – число, стоящее во второй строке и первом столбце.

Свойства определителей второго порядка: 1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами. 2. При перестановке двух строк (или столбцов) определитель изменит знак на противоположный, сохраняя абсолютную величину. 3. Определитель с двумя одинаковыми строками и столбцами равен нулю. 4. Общий множитель всех элементов строки или столбца можно выносить за знак определителя; если все элементы какой-то строки или столбца равны 0, то и определитель равен 0. 5. Если к элементам какой либо строки (или столбца) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель не изменит своей величины.

Практические занятия

1. Вычисление определителей третьего порядка

Задания для самостоятельного выполнения

1. Конспект на тему: Системы линейных уравнений. Метод подстановки.

Форма контроля самостоятельной работы:

• Устный опрос

Вопросы для самоконтроля по теме:

1. Как составляется определитель второго порядка и каким знаком он обозначается?