1.5.2. Формы записи комплексных чисел

Основные понятия и термины: модуль комплексного числа

План изучения темы:

1. Устный опрос

2. Теоретическая часть

3. Практическая работа 16

4. Практическая работа 17

5. Самостоятельная работа

Краткое изложение теоретических вопросов:

Любое комплексное число (кроме нуля)  можно записать в тригонометрической форме: , где  – это модуль комплексного числа, а  – аргумент комплексного числа.

Любое комплексное число (кроме нуля)  можно записать в показательной форме:

Практические занятия

1. Возведение комплексных чисел в степень.

2. Извлечение из корня комплексных чисел

Задания для самостоятельного выполнения

1. Конспект на тему: Возведение комплексных чисел в степень

Форма контроля самостоятельной работы:

• Устный опрос

• Проверка тетрадей

Вопросы для самоконтроля по теме:

1. Как геометрически представляется комплексное число?

2. Что называется модулем комплексного числа?

3. Как выполняется сложение и вычитание комплексных чисел?

4. Как выполняется умножение комплексных чисел?

5. Как выполняется деление комплексных чисел?

6. Как выполняется возведение в степень мнимых и комплексных чисел?

Раздел 2. Функции и графики

Тема 2.1. Построение графиков функций

2.1.1. Графики показательных функций

Основные понятия и термины: показательная функция

План изучения темы:

1. Устный опрос

2. Теоретическая часть

3. Решение задач

Краткое изложение теоретических вопросов:

y = a^x, где a>0, a≠ 1

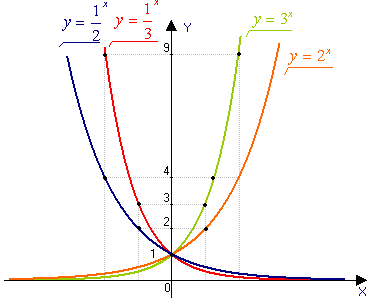
Свойства показательной функции.

Определение. Функция, заданная формулой у=а^х (где а>0, а≠1), называется показательной функцией с основанием а. Пусть a — неотрицательное число, x — рациональное число: . Тогда определяется по следующим правилам.

• Если x> 0, то .

• 

• 

• 

• 

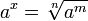Практические занятия не предусмотрены

Задания для самостоятельного выполнения

Конспекты на темы:

1. Графики линейных функций

2. Графики квадратичных функций

Форма контроля самостоятельной работы:

• Устный опрос

• Проверка тетрадей

Вопросы для самоконтроля по теме:

1. Укажите область определения и множество значений показательной функции

2. Перечислите основные свойства показательной функции

3. Постройте график функции у=0,2^х +1

2.1.2. Графики логарифмических функций

Основные понятия и термины: логарифмическая функция

План изучения темы:

1. Устный опрос

2. Теоретическая часть

3. Практическая работа 18

4. Практическая работа 19

5. Практическая работа 20

6. Самостоятельная работа

Краткое изложение теоретических вопросов:

Показательная функция у= (a>0,a≠1) является монотонной, поэтому она имеет обратную функцию, чтобы найти эту функцию нужно из формулы : у= выразить х через у.

х=

Функция у= a>0, a≠1) называется логарифмической

И так, показательная и логарифмическая функция при данном и том же основании является взаимно обратными функциями.

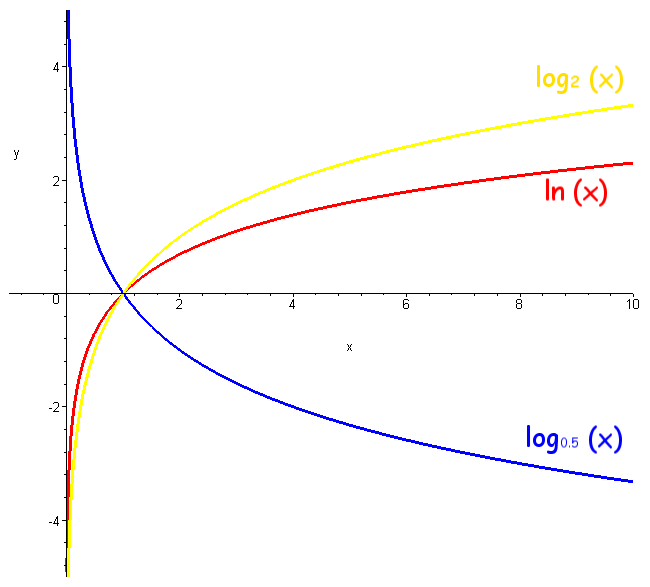
График логарифмической функции у= можно построить, воспользовавшись тем, что график у= обратная показательной функции у= . Поэтому достаточно построить график функции у= ,а затем отобразить его симметрично относительно прямой.

У= у=

а>1 0<a<1

x		1	2	4
у	1	0	-1	-2

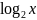y= у=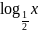

x	1	2	4
y	0	1	2	-1

Практические занятия:

1. Графики функций y=sin x и y=cos x

2. Построение графиков функций y=tg x и y=ctg x

3. Построение графиков обратных тригонометрических функций

Задания для самостоятельного выполнения

1. Конспект на тему: Графическое решение уравнений

Форма контроля самостоятельной работы:

• Устный опрос

• Проверка тетрадей

Вопросы для самоконтроля по теме:

1. Как связаны между собой графики показательной и логарифмической функций?

2. Укажите область определения и множество значений логарифмической функции.

3. Перечислите основные свойства логарифмической функции.

4. Постройте график функции у=log_0,5 x +1