6.4.4. Площади поверхностей и объем конуса
Основные понятия и термины: конус, боковая поверхность конуса, основание конуса
План изучения темы:
1. Устный опрос
2. Теоретическая часть
3. Практическая работа 65
4. Практическая работа 66
Краткое изложение теоретических вопросов:
Площадь поверхности конуса (или просто поверхность конуса) равна сумме площадей основания и боковой поверхности.
Площадь боковой поверхности конуса вычисляется по формуле: S = πRl, где R — радиус основания конуса, а l — образующая конуса.
Так как площадь основания конуса равна πR2 (как площадь круга), то площадь полной поверхности конуса будет равна: πR2 + πRl = πR (R + l ).
Объем
конуса
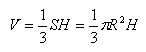
Практические занятия
1. Площади поверхностей конуса
2. Объем конуса
Задания для самостоятельного выполнения:
Вычислить полную поверхность конуса и его объём по данным, помещённым в нижеследующей таблице:
|
Радиус основания |
Длина образующей |
Полная поверхность |
Объём
|
1 |
3см |
10 см |
... |
... |
2 |
5 см |
13 см |
... |
... |
3 |
10 см |
20 см |
... |
... |
4 |
11 см |
35 см |
... |
... |
Форма контроля самостоятельной работы:
Устный опрос
Проверка тетрадей
Вопросы для самоконтроля по теме:
1. Какое тело называется конусом?
2. Что принимается в качестве площади боковой поверхности конуса?
3. Выпишите формулы для вычисления площадей боковой и полной поверхностей конуса.
6.4.5. Усеченный конус
Основные понятия и термины: усечённый конус
План изучения темы:
1. Устный опрос
2. Теоретическая часть
3. Решение задач
Краткое изложение теоретических вопросов:
Усеченный конус – часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.
Основание полного конуса и круг, по которому секущая плоскость пересекает полный конус, называются основаниями усеченного конуса; отрезок прямой, перпендикулярной основаниям и заключенный между ними, называется высотой усеченного конуса, длина этого отрезка также называется высотой усеченного конуса.
Усеченный конус получается, если от полного конуса "отсечь" подобный ему конус плоскостью, параллельной основанию. Значит, и боковую поверхность, и объем усеченного конуса можно вычислить, зная коэффициент подобия, а также боковую поверхность и объем полного конуса.
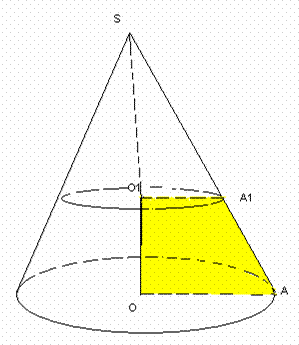
Плоскость, перпендикулярная оси конуса, отсекает от него меньший конус. Оставшуюся часть называют усеченным конусом. Усеченный конус можно получить и как тело вращения.
Усеченным конусом называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям.
Круги O и O1 - его основания, его образующие AA1 равны между собой, прямая OO1 - ось, отрезок OO1 - высота. Его осевое сечение - равнобедренная трапеция.
Площадь
боковой поверхности
усеченного конуса: S=
(R1+R2)l
Объем
усеченного конуса:
V=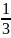
H(R12+R
1R
2+R22),
где h - высота усеченного конуса; R1,R2
- радиусы верхнего и нижнего оснований;
l - образующая.
Практические занятия не предусмотрены
Задания для самостоятельного выполнения:
1. Найдите, чему равна площадь осевого сечения и площадь боковой поверхности усеченного конуса, если радиусы его оснований 3 и 6 см, а высота равна 4 см.
2. Найдите, чему равна осевого сечения и полной поверхности усеченного конуса, образующая равна 30 см, а диагональ осевого сечения равная 40 см перпендикулярна с образующей.
3. Радиусы оснований усеченного конуса равны 16 см и 25 см. Найдите площадь полной поверхности конуса, если в его осевое сечение можно вписать окружность.
Форма контроля самостоятельной работы:
Устный опрос
Проверка тетрадей
Вопросы для самоконтроля по теме:
1. Какое тело называется усечённым конусом?
2. Дайте определение высоты усечённого конуса.
3. Как вычисляется площадь боковой поверхности усечённого конуса.