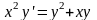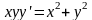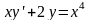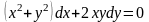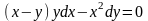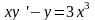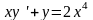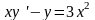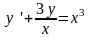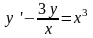- •Учебно-методический комплекс по дисциплине математика
- •270802 Строительство и эксплуатация зданий и сооружений
- •Для студентов очной формы обучения Альметьевск, 2012
- •Содержание
- •Уважаемый студент!
- •Раздел 1 алгебра
- •Тема 1.1 Элементы вычислительной математики
- •1.1.2. Приближенные значения величин
- •Тема 1.2. Корень. Степень
- •1.2.1. Корень n-ой степени.
- •1.2.2. Степень с рациональным показателем
- •Тема 1.3. Логарифмы
- •Понятие о логарифме числа.
- •Тема 1.4. Тригонометрия
- •Радианная и градусная меры углов
- •1.4.2. Формулы двойного аргумента
- •Тема 1.5. Комплексные числа
- •1.5.1. Понятие о мнимых и комплексных числах.
- •1.5.2. Формы записи комплексных чисел
- •Раздел 2. Функции и графики
- •Тема 2.1. Построение графиков функций
- •2.1.1. Графики показательных функций
- •2.1.2. Графики логарифмических функций
- •Раздел 3. Уравнения и неравенства
- •Тема 3.1. Рациональные уравнения и неравенства
- •3.1.1. Квадратные уравнения и неравенства. Метод интервалов
- •3.1.2. Определители второго порядка
- •3.1.3. Решение систем двух уравнений методом Крамера
- •3.1.4. Метод Гаусса
- •3.1.5. Решение текстовых задач на составление уравнений
- •Тема 3.2. Показательные уравнения и неравенства
- •3.2.1. Простейшие показательные уравнения и неравенства
- •3.2.2. Применение свойств степеней.
- •3.2.3. Показательные уравнения и неравенства, сводящиеся к квадратным
- •Тема 3.3. Логарифмические уравнения и неравенства
- •3.3.1. Простейшие логарифмические уравнения и неравенства
- •3.3.3. Применение свойств логарифмов
- •3.3.4. Логарифмические уравнения и неравенства, сводящиеся к квадратным
- •3.3.5. Системы логарифмических уравнений
- •Тема 3.4. Тригонометрические уравнения и неравенства
- •3.4.1. Обратные тригонометрические функции.
- •3.4.4. Решение тригонометрических уравнений разложением на множители
- •3.4.5. Решение тригонометрических уравнений разными способами
- •3.4.6. Тригонометрические неравенства.
- •Раздел 4. Начала математического анализа
- •Тема 4.1. Пределы функции
- •4.1.1. Последовательности. Предел функции
- •4.1.2. I и II замечательные пределы
- •Тема 4.2. Производная
- •4.2.1. Приращение функции. Производная
- •4.2.2. Правила дифференцирования
- •Тема 4.3. Приложения производной
- •4.3.1. Физический смысл производной. Мгновенная скорость. Ускорение
- •4.3.2. Геометрический смысл производной. Уравнение касательной
- •4.3.3. Возрастание и убывание функции. Точки экстремума
- •4.3.4. Выпуклость графика функции. Точка перегиба
- •4.3.5. Асимптоты
- •Тема4.4. Неопределенный интеграл
- •4.4.1. Первообразная функция
- •4.4.2. Неопределенный интеграл
- •Тема4.5. Определенный интеграл
- •4.5.1. Формула Ньютона-Лейбница
- •4.5.2. Метод замены переменной
- •Тема4.6. Приложения определенного интеграла
- •4.6.1. Площадь криволинейной трапеции
- •4.6.2. Вычисление пути, пройденного телом
- •Тема 4.7. Дифференциальные уравнения
- •4.7.1. Основные понятия дифференциального уравнения
- •4.7.2. Линейные однородные дифференциальные уравнения первого порядка
- •4.7.3 Линейные неоднородные дифференциальные уравнения первого порядка
- •Раздел 5. Комбинаторика, статистика и теория вероятностей
- •Тема 5.1. Элементы комбинаторики и теория вероятностей
- •5.1.1. Перестановки и факториалы. Правило умножения
- •5.1.2. Сочетание и размещение
- •5.1.3. Вероятности случайных событий
- •5.1.4. Сложение и умножение вероятностей случайных событий
- •Тема 5.2. Математическая статистика
- •5.2.1. Задачи математической статистики
- •5.2.2. Центральные тенденции: среднее значение, мода, медиана
- •Раздел 6. Геометрия
- •Тема 6.1. Элементы векторной алгебры и аналитической геометрии
- •6.1.1. Векторы. Действия над векторами.
- •6.1.2. Скалярное произведение векторов
- •6.1.3. Векторное произведение векторов
- •6.1.4. Прямая линия на плоскости. Уравнения прямых
- •6.1.5. Линии второго порядка на плоскости
- •Тема 6.2. Прямая и плоскость в пространстве
- •6.2.1. Аксиомы стереометрии
- •6.2.2. Взаимное расположение прямых и плоскостей в пространстве
- •Тема 6.3. Многогранники
- •6.3.1. Решение планиметрических задач
- •6.3.2. Призма.
- •6.3.3. Параллелепипед
- •Основные элементы
- •6.3.4. Пирамида.
- •6.3.5. Усеченная пирамида
- •6.3.6. Правильные многогранники
- •Тема 6.4. Тела вращения
- •6.4.1. Цилиндр
- •6.4.2. Площади поверхностей и объем цилиндра
- •6.4.3. Конус
- •6.4.4. Площади поверхностей и объем конуса
- •6.4.5. Усеченный конус
- •6.4.6. Шар и сфера
- •Контроль и оценка результатов освоения дисциплины Текущий контроль
- •Итоговый контроль Вопросы к дифференцированному зачету
- •Вопросы к экзамену
- •Глоссарий Абсолютная погрешность - разность между приближенным числом и его точным значением (из большего числа вычитается меньшее).
- •Информационное обеспечение дисциплины Основные источники
- •Дополнительные источники
4.7.2. Линейные однородные дифференциальные уравнения первого порядка
Основные понятия и термины: дифференциальные уравнения первого порядка
План изучения темы:
1. Устный опрос
2. Теоретическая часть
3. Практическая работа 51
Краткое изложение теоретических вопросов:
Однородным
дифференциальным уравнением
называется
уравнение вида:
 .
.
При
решении однородных дифференциальных
уравнений сохраняя прежнюю независимую
переменную х,
вводят вспомогательную неизвестную
функцию t
по формуле:
 .
Откуда
.
Откуда
 .
.
Преобразуя
уравнение
,
получаем:
 .
Найдя отсюда выражение для t
как функции от x
возвращаются к переменной
,
получая при этом решение однородного
дифференциального уравнения.
.
Найдя отсюда выражение для t
как функции от x
возвращаются к переменной
,
получая при этом решение однородного
дифференциального уравнения.
Пример.
Решить уравнение
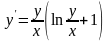 .
.
Делаем
замену:
 .
.
Подставляем
в исходное уравнение:

Разделяем
переменные:
 .
.
Интегрируя:
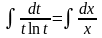 ,
получаем:
,
получаем:
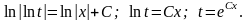
Переходя
от вспомогательной функции обратно к
функции у, получаем общее
решение:

Практические занятия
1. Решение дифференциальных уравнений
Задания для самостоятельного выполнения:
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
Форма контроля самостоятельной работы:
Устный опрос
Проверка тетрадей
Вопросы для самоконтроля по теме:
1. Алгоритм решения линейного однородного дифференциального уравнения первого порядка
4.7.3 Линейные неоднородные дифференциальные уравнения первого порядка
Основные понятия и термины: однородные дифференциальные уравнения первого порядка, неоднородные дифференциальные уравнения первого порядка
План изучения темы:
1. Устный опрос
2. Теоретическая часть
3. Самостоятельная работа
Краткое изложение теоретических вопросов:
Дифференциальное
уравнение называется линейным
относительно неизвестной функции и ее
производной, если оно может быть записано
в виде:
 .
При этом, если правая часть Q(x)
равна нулю, то такое уравнение называется
линейным
однородным
дифференциальным
уравнением, если правая часть Q(x)
не равна нулю, то такое уравнение
называется линейным
неоднородным
дифференциальным
уравнением (P(x)
и
Q(x)
–
функции, непрерывные на некотором
промежутке a
< x
< b).
.
При этом, если правая часть Q(x)
равна нулю, то такое уравнение называется
линейным
однородным
дифференциальным
уравнением, если правая часть Q(x)
не равна нулю, то такое уравнение
называется линейным
неоднородным
дифференциальным
уравнением (P(x)
и
Q(x)
–
функции, непрерывные на некотором
промежутке a
< x
< b).
Метод
Бернулли.
Суть
метода заключается в том, что искомая
функция представляется в виде произведения
двух функций
 ,
где u=u(x)
и v=v(x)
– неизвестные функции от х.
Отсюда,
,
где u=u(x)
и v=v(x)
– неизвестные функции от х.
Отсюда,
 .
.
Подставляя
у
и
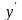 в
исходное уравнение, получаем:
в
исходное уравнение, получаем:
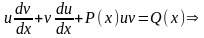
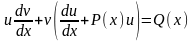 .
.
В
качестве u
берут частное решение уравнения:
 .
Решая это дифференциальное уравнение,
определяем u:
.
Решая это дифференциальное уравнение,
определяем u:

 .
.
Для нахождения второй неизвестной функции v подставим полученное выражение для функции u в исходное уравнение с учетом того, что выражение, стоящее в скобках, равно нулю.
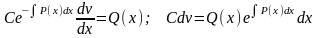 .
.
Интегрируя,
получаем функцию v:
 .
.
Подставляя полученные значения u и v в y=uv, получаем:
 .
.
Окончательно
получаем формулу:
 .
.
Это уравнение является решением неоднородного линейного дифференциального уравнения в общем виде по способу Бернулли.
Пример.
Решить уравнение
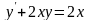 .
.
Решение.
Полагаем и .
Тогда

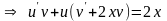 .
.
1)
 ,
,
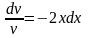 ,
,
 ,
,
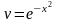 .
.
2)
 ,
т.е.
,
т.е.
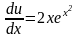 ,
,
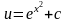 .
.
Итак,
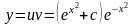 .
.
Практические занятия не предусмотрены
Задания для самостоятельного выполнения:
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
Форма контроля самостоятельной работы:
Устный опрос
Проверка тетрадей
Вопросы для самоконтроля по теме:
1. Алгоритм решения линейного неоднородного дифференциального уравнения первого порядка