
- •Учебно-методический комплекс по дисциплине математика
- •270802 Строительство и эксплуатация зданий и сооружений
- •Для студентов очной формы обучения Альметьевск, 2012
- •Содержание
- •Уважаемый студент!
- •Раздел 1 алгебра
- •Тема 1.1 Элементы вычислительной математики
- •1.1.2. Приближенные значения величин
- •Тема 1.2. Корень. Степень
- •1.2.1. Корень n-ой степени.
- •1.2.2. Степень с рациональным показателем
- •Тема 1.3. Логарифмы
- •Понятие о логарифме числа.
- •Тема 1.4. Тригонометрия
- •Радианная и градусная меры углов
- •1.4.2. Формулы двойного аргумента
- •Тема 1.5. Комплексные числа
- •1.5.1. Понятие о мнимых и комплексных числах.
- •1.5.2. Формы записи комплексных чисел
- •Раздел 2. Функции и графики
- •Тема 2.1. Построение графиков функций
- •2.1.1. Графики показательных функций
- •2.1.2. Графики логарифмических функций
- •Раздел 3. Уравнения и неравенства
- •Тема 3.1. Рациональные уравнения и неравенства
- •3.1.1. Квадратные уравнения и неравенства. Метод интервалов
- •3.1.2. Определители второго порядка
- •3.1.3. Решение систем двух уравнений методом Крамера
- •3.1.4. Метод Гаусса
- •3.1.5. Решение текстовых задач на составление уравнений
- •Тема 3.2. Показательные уравнения и неравенства
- •3.2.1. Простейшие показательные уравнения и неравенства
- •3.2.2. Применение свойств степеней.
- •3.2.3. Показательные уравнения и неравенства, сводящиеся к квадратным
- •Тема 3.3. Логарифмические уравнения и неравенства
- •3.3.1. Простейшие логарифмические уравнения и неравенства
- •3.3.3. Применение свойств логарифмов
- •3.3.4. Логарифмические уравнения и неравенства, сводящиеся к квадратным
- •3.3.5. Системы логарифмических уравнений
- •Тема 3.4. Тригонометрические уравнения и неравенства
- •3.4.1. Обратные тригонометрические функции.
- •3.4.4. Решение тригонометрических уравнений разложением на множители
- •3.4.5. Решение тригонометрических уравнений разными способами
- •3.4.6. Тригонометрические неравенства.
- •Раздел 4. Начала математического анализа
- •Тема 4.1. Пределы функции
- •4.1.1. Последовательности. Предел функции
- •4.1.2. I и II замечательные пределы
- •Тема 4.2. Производная
- •4.2.1. Приращение функции. Производная
- •4.2.2. Правила дифференцирования
- •Тема 4.3. Приложения производной
- •4.3.1. Физический смысл производной. Мгновенная скорость. Ускорение
- •4.3.2. Геометрический смысл производной. Уравнение касательной
- •4.3.3. Возрастание и убывание функции. Точки экстремума
- •4.3.4. Выпуклость графика функции. Точка перегиба
- •4.3.5. Асимптоты
- •Тема4.4. Неопределенный интеграл
- •4.4.1. Первообразная функция
- •4.4.2. Неопределенный интеграл
- •Тема4.5. Определенный интеграл
- •4.5.1. Формула Ньютона-Лейбница
- •4.5.2. Метод замены переменной
- •Тема4.6. Приложения определенного интеграла
- •4.6.1. Площадь криволинейной трапеции
- •4.6.2. Вычисление пути, пройденного телом
- •Тема 4.7. Дифференциальные уравнения
- •4.7.1. Основные понятия дифференциального уравнения
- •4.7.2. Линейные однородные дифференциальные уравнения первого порядка
- •4.7.3 Линейные неоднородные дифференциальные уравнения первого порядка
- •Раздел 5. Комбинаторика, статистика и теория вероятностей
- •Тема 5.1. Элементы комбинаторики и теория вероятностей
- •5.1.1. Перестановки и факториалы. Правило умножения
- •5.1.2. Сочетание и размещение
- •5.1.3. Вероятности случайных событий
- •5.1.4. Сложение и умножение вероятностей случайных событий
- •Тема 5.2. Математическая статистика
- •5.2.1. Задачи математической статистики
- •5.2.2. Центральные тенденции: среднее значение, мода, медиана
- •Раздел 6. Геометрия
- •Тема 6.1. Элементы векторной алгебры и аналитической геометрии
- •6.1.1. Векторы. Действия над векторами.
- •6.1.2. Скалярное произведение векторов
- •6.1.3. Векторное произведение векторов
- •6.1.4. Прямая линия на плоскости. Уравнения прямых
- •6.1.5. Линии второго порядка на плоскости
- •Тема 6.2. Прямая и плоскость в пространстве
- •6.2.1. Аксиомы стереометрии
- •6.2.2. Взаимное расположение прямых и плоскостей в пространстве
- •Тема 6.3. Многогранники
- •6.3.1. Решение планиметрических задач
- •6.3.2. Призма.
- •6.3.3. Параллелепипед
- •Основные элементы
- •6.3.4. Пирамида.
- •6.3.5. Усеченная пирамида
- •6.3.6. Правильные многогранники
- •Тема 6.4. Тела вращения
- •6.4.1. Цилиндр
- •6.4.2. Площади поверхностей и объем цилиндра
- •6.4.3. Конус
- •6.4.4. Площади поверхностей и объем конуса
- •6.4.5. Усеченный конус
- •6.4.6. Шар и сфера
- •Контроль и оценка результатов освоения дисциплины Текущий контроль
- •Итоговый контроль Вопросы к дифференцированному зачету
- •Вопросы к экзамену
- •Глоссарий Абсолютная погрешность - разность между приближенным числом и его точным значением (из большего числа вычитается меньшее).
- •Информационное обеспечение дисциплины Основные источники
- •Дополнительные источники
Раздел 4. Начала математического анализа
Тема 4.1. Пределы функции
4.1.1. Последовательности. Предел функции
Основные понятия и термины: последовательность, предел функции
План изучения темы:
1. Устный опрос
2. Теоретическая часть
3. Практическая работа 33
4. Практическая работа 34
Краткое изложение теоретических вопросов:
Рассмотрим
последовательность

a1=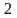 ;
a2=
;
a2= ;
a3=
;
a3=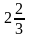 ;
а4=
;
а4=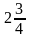 ;
а5=
;
а5= …
а100=
…
а100=
В
этой последовательности при n
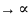 аn
аn
 3
3


Пример: Вычислить предел:
1)
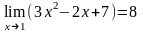
2)

3)

Практические занятия:
1. Раскрытие неопределенности ∞/∞
2. Раскрытие неопределенности 0/0
Задания для самостоятельного выполнения
Составить конспект на тему: Раскрытие неопределенностей
Форма контроля самостоятельной работы:
Устный опрос
Проверка тетрадей
Вопросы для самоконтроля по теме:
1. Как символически записывается определение предела?
2. Может ли последовательность иметь два разных предела?
4.1.2. I и II замечательные пределы
Основные понятия и термины: первый замечательный предел, второй замечательный предел
План изучения темы:
1. Устный опрос
2. Теоретическая часть
3. Практическая работа 35
Краткое изложение теоретических вопросов:
Первый замечательный предел:
![]()
Второй замечательный предел:
![]()
Пример. Найти пределы:
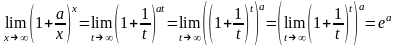
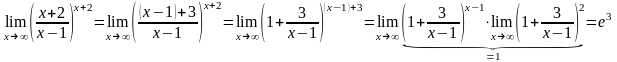
Практические занятия: 1. Вычисление пределов
Задания для самостоятельного выполнения
Составить конспекты на темы:
1. Первый замечательный предел
2. Второй замечательный предел
Форма контроля самостоятельной работы:
Устный опрос
Проверка тетрадей
Вопросы для самоконтроля по теме:
1. Сформулируйте первый замечательный предел.
2. Сформулируйте второй замечательный предел.
Тема 4.2. Производная
4.2.1. Приращение функции. Производная
Основные понятия и термины: производная функции
План изучения темы:
1. Устный опрос
2. Теоретическая часть
3. Практическая работа 36
Краткое изложение теоретических вопросов:
При сравнении значения функции f в некоторой фиксированной точке x0 со значениями этой функции в различных точках x, лежащих в окрестности x0, удобно выражать разность f(x) – f(x0) через разность x – x0, пользуясь понятиями «приращение аргумента» и «приращение функции».
Пусть x – произвольная точка, лежащая в некоторой окрестности фиксированной точки x0. Разность x – x0 называется приращением независимой переменной (или приращением аргумента) в точке x0 и обозначается Δx. Таким образом, Δx = x –x0, откуда следует, что x = x0 + Δx.
Говорят также, что первоначальное значение аргумента x0 получило приращение Δx. Вследствие этого значение функции f изменится на величину f(x) – f(x0) = f (x0 +Δx) – f(x0).
Эта разность называется приращением функции f в точке x0, соответствующим приращению Δx, и обозначается символом Δf (читается «дельта эф»), т.е. по определению Δf = f (x0 + Δx) – f (x0), откуда f (x) = f (x0 +Δx) = f (x0) + Δf.
При фиксированном x0 приращение Δf есть функция от Δx. Δf называют также приращение зависимой переменной.
Предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю (если этот предел существует), представляет собой первую производную этой функции по данному аргументу. Поэтому формулу запишем в виде:
уꞌ=
-
Функция
Производная
с
0
х
1
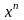
n

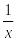
-
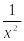
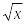
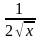
sin x
cos x
cos x
- sin x
tg x
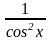
ctg x
-
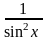
arcsin x

arccos x
-
arctg x
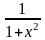
arcctg x
-
a
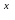
a
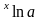
e
e
log
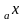
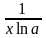
ln x

Практические занятия:
1. Применение формул дифференцирования
Задания для самостоятельного выполнения
Составить конспект на тему: Производная функции
Форма контроля самостоятельной работы:
Устный опрос
Проверка тетрадей
Вопросы для самоконтроля по теме:
1. Что называется приращением аргумента?
2. Что называется приращением функции?
3. Что называется производной функции?
4. Как называется процесс вычисления производной?
