Определение удельной работы колеса с конечным числом лопаток.
Удельная теоретическая работа колеса с конечным числом лопаток и отсутствием закрутки потока перед входом определяется по такой же формуле, что и для колеса с бесконечным числом лопаток:
.
Проблема использования этой формулы состоит в том, что cu2 для колеса с z≠∞ не может быть определена так же просто, как cu2∞.
Для определения cu2∞ из треугольника скоростей на выходе при известной cm2 достаточно знания угла β2, который определяется чисто из геометрических параметров лопасти. Для определения cu2 из аналогичного треугольника необходим угол β2ср, который определяется как угол усредненного вектора течения реального потока на выходе из колеса и не является простой функцией геометрических параметров колеса. Как уже сказано выше, угол β2ср уменьшается по сравнению с β2 из-за влияния циркуляционного потока и разницы давлений в межлопастном канале. Эти влияния могут быть названы также влиянием конечного числа лопастей рабочего колеса. Существует несколько известных методик учёта этого влияния. В общем случае его учитывают коэффициентом kz:
.
В соответствии с записанным выражением и уравнениями Эйлера для колёс с отсутствием закрутки потока перед колесом можно записать:
Коэффициент kz определяют по разным методикам. Применяются приближённые зависимости Проскуры, Стодолы, Майзеля и Пфляйдерера. Кроме того, используются более точные экспериментальные данные для колёс с подобными геометрическими формами, представленные различными исследователями в виде таблиц и графиков.
В соответствии с методикой Пфляйдерера рассматриваемое влияние учитывается следующим приближённым выражением:
,
где L∞, Lт – удельные теоретические работы колёс с бесконечным и конечным числами лопастей (определяемые по струйной теории на основании уравнения Эйлера); p – поправка на конечное число лопастей.
В соответствии с записанным выражением и уравнениями Эйлера для колёс с отсутствием закрутки потока перед колесом можно записать:
,
откуда 
;
.
Поправка р зависит от числа лопастей, угла установки лопасти на выходе, от квадрата соотношения радиусов R1/ R2, а также от чистоты поверхности лопастей.
.
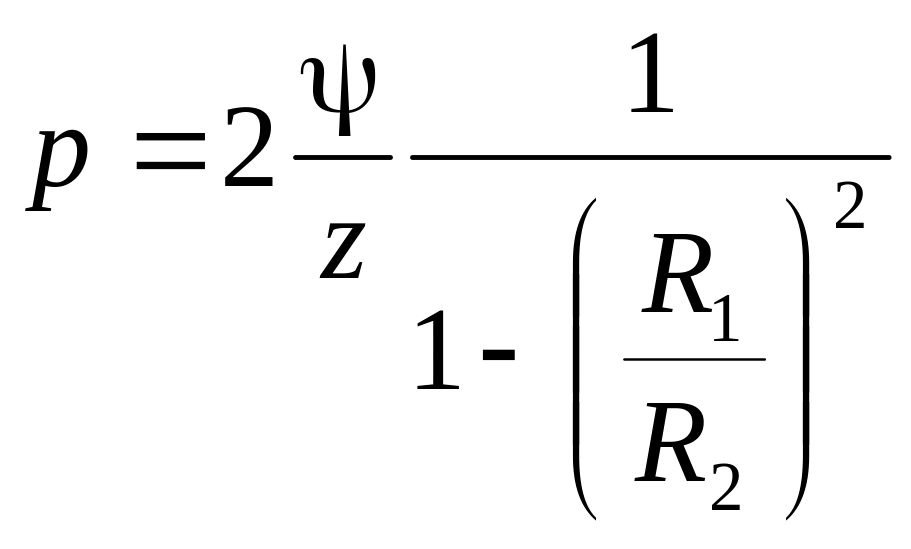Коэффициент ψ для колёс с лопастями, загнутыми назад, равен
,
где 0,55 принимается для колёс с более чистой поверхностью, а большие значения – для лопаток с относительно более высокой шероховатостью внутренней поверхности каналов.
Стодола и Майзель определяли поправку на основе учёта влияния вихревого движения в межлопастном канале. В соответствии с предложенным ими подходом
,
Откуда 
.
Определение диаметра колеса центробежного насоса при известном значении действительной удельной работы колеса.
Если известна величина действительной удельной работы L, то можно определить наружный диаметр колеса насоса при известном числе лопастей z, известной угловой скорости вращения колеса ω и известном угле установки лопасти на выходе β2. Как известно из определений КПД насоса,
.
Записанное выражение устанавливает связь между действительной работой колеса и работой колеса с бесконечным числом лопастей на основе установленных выше зависимостей. Удельная работа колеса с бесконечным числом лопаток может быть определена при известном значении угла установки лопасти на выходе β2, если известна расходная составляющая скорости на выходе из колеса cm2. Эта величина обычно близка к расходной составляющей абсолютной скорости на входе cm1, а для колёс с отсутствием закрутки потока перед входом в колесо cm1= c10 (см. рис. 10). Что касается c10, то она близка к скорости потока на входе в насос, рекомендации по выбору которой будут рассмотрены далее, и которая может быть установлена достаточно просто и однозначно в начале проектирования насоса на основании обычного в таких случаях набора исходных данных.
Итак, чтобы определить L∞ как функцию β2 и cm2, следует рассмотреть выходной треугольник скоростей при z = ∞ (см. рис. 9). Из решения треугольника получим
.
Далее, на основании уравнения Эйлера получим
.
В результате получим квадратичное уравнение
.
Это уравнение решается относительно окружной скорости u2:
.
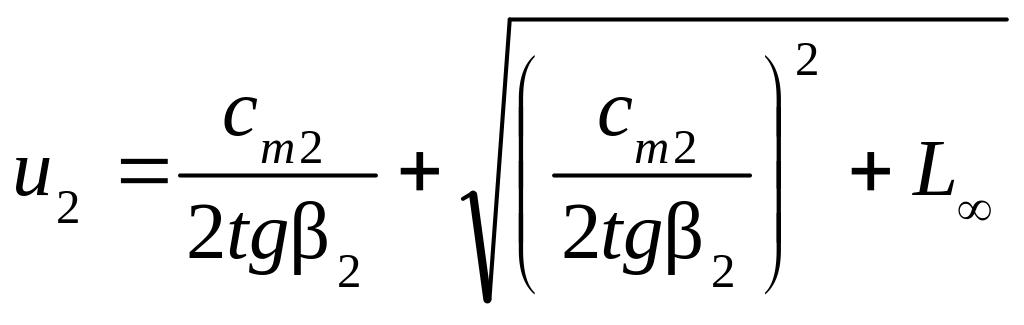С учётом записанной выше зависимости между действительной удельной работой колеса и L∞ можно записать
.
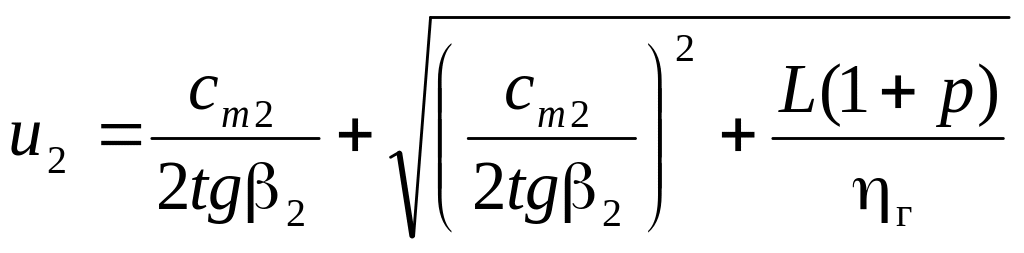В последнем выражении поправка р на конечное число лопастей определяется с учётом действительного значения z и прочих факторов, от которых она зависит (см. ранее изложенное о влиянии числа лопастей на удельную работу колеса). При известной окружной и угловой скорости ротора наружный диаметр колеса находится из выражения
.
Как следует из приведенных выражений, при определении наружного диаметра колеса необходимо задавать угол установки лопатки на выходе из колеса β2 и расходную составляющую скорости cm2. Кроме того, необходимо задаваться числом лопастей z, выбирать угловую скорость ротора ω и скорость жидкости на входе в колесо. Все эти величины выбираются и определяются с учётом их влияния на работу проектируемого насоса по рекомендациям, связывающих это влияния не только с качественными, но и с количественными показателями. Соответствующие рекомендации разработаны на основе обобщения огромного экспериментального материала, а обработан этот материал на основе так называемой теории подобия. Для того, чтобы успешно пользоваться рекомендациями этой теории, следует рассмотреть её основы.
Конец