Системы массового обслуживания с отказами. Формулы Эрланга

Рассмотрим часто встречающийся класс случайных процессов – процесс гибели и размножения. Такое название процесс получил ввиду того, что он является математической моделью задач об изменении численности биологических популяций. Граф состояний процесса гибели и размножения изображен на рис. 23.1.

Рис. 23.1

Переходы могут осуществляться только в состояния с соседними номерами. При решении упомянутых выше биологических задач полагают, что состояние соответствует численности популяции, равной k, и переход системы в состояние происходит при рождении одного члена популяции, а переход в состояние – при гибели одного члена популяции.

Для размеченного графа, представленного на рис. 23.1, составим систему уравнений для предельных вероятностей состояний. Согласно алгоритму составления таких уравнений, описанному в предыдущей лекции, получим:

(для состояния ), (23.1)

и

(для состояния ).

Последнее соотношение с учетом (23.1) приводится к виду:

(для состояния ). (23.2)

По аналогии с уравнениями (23.1) и (23.2) получают уравнения для остальных состояний системы. В результате имеем следующую систему уравнений

. (23.3)

к которой добавляется нормировочное условие

. (23.4)

Решим систему уравнений (23.3), (23.4).

Из (23.3) найдем

. (23.5)

Подставив из (23.5) в (23.4), получим

. (23.6)

Соотношения (23.6) и (23.5) описывают предельные вероятности всех состояний системы.

Система массового обслуживания с отказами

Показателями эффективности в СМО с отказами являются следующие параметры:

– вероятность отказа, определяемая как предельная вероятность того, что заявки покинет СМО необслуженной;

 – относительная пропускная способность или вероятность того, что заявка будет обслужена;

A – абсолютная пропускная способность СМО, определяемая соотношением и характеризующая среднее число заявок, обслуживаемых в единицу времени;

 – среднее число занятых каналов.

Сначала рассмотрим простейший случай СМО с отказами – одноканальную систему с отказами. Ее размеченный граф состояний представлен на рис. 23.2.

Рис. 23.2

Система S (СМО) имеет два состояния: – канал свободен, – канал занят. Поток заявок поступает с интенсивностью , а поток обслуживания имеет интенсивность . Все потоки событий предполагаются простейшими.

Составим систему алгебраических уравнений для предельных вероятностей состояний системы (23.3):

которая вырождается в одно уравнение. Добавим к нему нормировочное условие (23.4): . Из этих соотношений получим

, . (23.7)

Найденные предельные вероятности состояний, очевидно, определяют вероятности обслуживания и отказа, т. е.

, (23.8)

. (23.9)

Абсолютная пропускная способность одноканальной СМО с отказами вычисляется по формуле:

. (23.10)

Теперь рассмотрим многоканальную систему с отказами. Решим классическую задачу Эрланга.

На n каналов поступает поток заявок с интенсивностью . Поток обслуживания имеет интенсивность . Найти предельные вероятности состояний системы и показатели ее эффективности. Через , обозначим состояние системы S (СМО), когда в ней находится k заявок, т. е. занять k каналов.

Размеченный граф состояний системы S соответствует процессу гибели и размножения и представлен на рис. 23.3.

Рис. 23.3

Поток заявок переводит систему S из любого левого состояния в правое с постоянной интенсивностью . Интенсивность потока обслуживаний, переводящих S из любого правого состояния в левое, постоянно меняется и равна для состояния . Действительно, если S находится в состоянии (два канала заняты), то она может перейти в состояние (один канал занят), когда закончит обслуживание либо первый, либо второй канал, т. е. суммарная интенсивность их потоков обслуживаний будет . Аналогично суммарный поток обслуживаний, переводящий СМО из состояния (три канала заняты) в , будет иметь интенсивность , т. е. может освободиться любой из трех каналов и т. д.

По формулам (23.6) и (23.5) для процесса гибели и размножения находим предельные вероятности для всех состояний S:

(23.11)

или обозначим

(23.12)

(23.13)

Величина  в формуле (23.12) называется интенсивностью нагрузки канала.

Формулы (23.13) называют формулами Эрланга.

Вычислим показатели эффективности СМО:

вероятность отказа –

, (23.14)

относительная пропускная способность –

, (23.15)

абсолютная пропускная способность –

, (23.16)

среднее число занятых каналов –

. (23.17)

Пример 23.1. Наблюдения показали, что в течение часа 15 студентов обращаются к информационно-поисковой программе читального зала академии. Средняя продолжительность поиска информации составляет 8 мин. Определить показатели эффективности поиска информации в читальном зале при наличии одного компьютера. Найти число компьютеров, для которых вероятность того, что будет обслужен, составит не менее 0,90.

Решение. По условию задачи интенсивность потока посещений – 1/час, интенсивность потока обслуживаний – 1/час. При наличии одного компьютера вероятность отказа в обслуживании вычислим по формуле (23.9):

.

Вероятность того, что студент будет обслужен, определяется по формуле (23.8):

.

Среднее число заявок в течение часа согласно формуле (23.10) составит

.

По полученным показателям эффективности поиска информации на одном компьютере можно говорить о неудовлетворительном обслуживании студентов.

Для его улучшения до требуемого уровня от до , необходимо увеличить число компьютеров n. Иными словами надо перейти от одноканальной СМО к многоканальной. Для определения минимального значения n воспользуемся формулами (23.13) и (23.15):

• при : ; ;

;

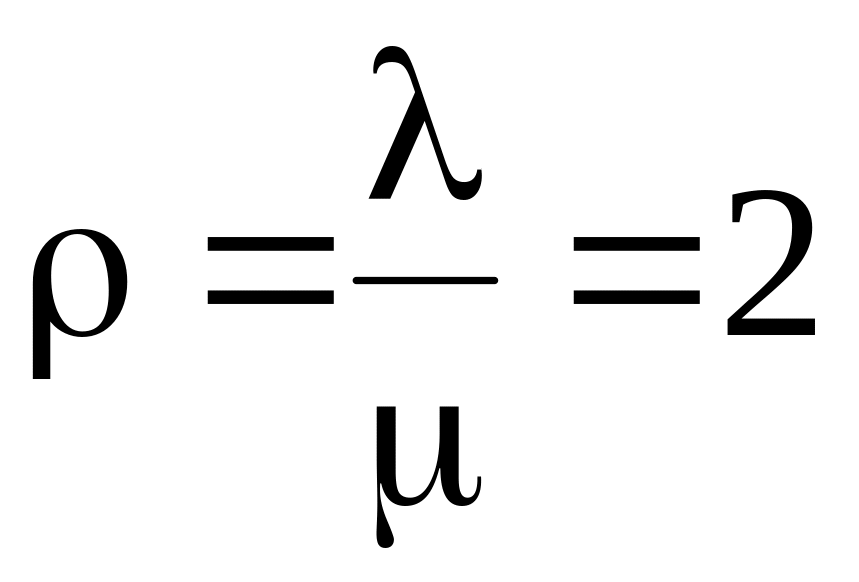• при : ; ;

.

Таким образом, условие задачи выполняется при наличии в читальном зале 4 компьютеров. При этом в час по формуле (23.16) будут обслуживаться в среднем студентов, а по формуле (23.17) будут заняты в среднем компьютера.