Квантовая физика

1. Дайте определение теплового излучения

Тепловое излучение – это излучение электромагнитных волн за счёт внутренней энергии.

2. Дайте определение потока энергии

Поток энергии – это энергия, испускаемая телом в единицу времени.

Ф=dW/dt, Ф=W/t, [Ф]=Вт

3. Дайте определение энергетической светимости

Энергетическая светимость R – величина, равная потоку энергии, испускаемой единицей поверхности тела по всем направлениям, во всем интервале частот.

R=dФ/dS, [R]=Вт/м²

4. Дайте определение испускательной способности тела

Испускательная способность тела – величина, равная энергетической светимости тела в единичном интервале частот или длин волн.

r_ω,Т=dR_T/dω, r_λ,T=dR_T/dλ

5. Дайте определение поглощательной способности тела

Поглощательная способность – величина, равная отношению потока энергии, поглощенного телом, к падающему потоку.

a_ω,T=Ф_погл/Ф_пад ≤1

6. Дайте определение абсолютно чёрного тела

Абсолютно чёрное тело – это тело, которое поглощает все падающее на него лучи.

Поглощательная способность АЧТ = 1.

7. Сформулируйте закон Кирхгофа (дайте определение и запишите формулу)

Закон Кирхгофа: Отношение испускательной способности к поглощательной способности не зависит от природы тела и для всех тел является универсальной функцией частоты и температуры.

(r_ω,Т/ a_ω,T)₁=(r_ω,Т/ a_ω,T)₂=…=ƒ(ω,Т)

8. Сформулируйте закон Стефана-Больцмана (дайте определение и запишите формулу)

Закон Стефана-Больцмана: Энергетическая светимость абсолютно чёрного тела прямо пропорциональна четвертой степени абсолютной температуры.

R=σT⁴, где σ = 5,67·10^-8 Вт/м²·К⁴

9. Сформулируйте 1-ый закон Вина (дайте определение и запишите формулу)

Первый закон Вина: Длина волны, на которую приходится максимум спектральной плотности энергетической светимости, с повышением температуры смещается в сторону коротких волн.

λ_{max r λ,T}= в/Т, где в = 2,9·10^-3 мК, λ=С₁/Т=в/Т

10. Сформулируйте 2-ой закон Вина (дайте определение и запишите формулу)

Второй закон Вина: Максимальное значение спектральной плотности энергетической светимости абсолютно чёрного тела прямо пропорционально пятой степени абсолютной температуры.

r_max=С₂·Т⁵, где С₂ = 1,29·10^-5 Вт/м²·мК⁵

11. Запишите уравнение Эйнштейна для фотоэффекта

ε = hν = ħω = A_вых + Т_max

ε = A_вых +

12. Сформулируйте гипотезу Планка (дайте определение и запишите формулу)

Атомы излучают энергию в виде порций – квантов, т.е. излучение носит дискретный характер.

Е = h = ħω

h = 6,62·10^-34 Дж·с, ħ = - постоянная Планка

– формула Планка.

13. Запишите выражение для энергии фотона

Е= hυ = ħω – энергия фотона.

14. Запишите выражение для импульса фотона

Р=(m )=E/C – импульс фотона.

15. Запишите закон сохранения энергии для эффекта Комптона

E + mc² = E^’+ mc² + T

16. Запишите закон сохранения импульса для эффекта Комптона

ħk = ħk^’ + p_e

17. Запишите выражение для длины волны смещённой компоненты излучения в эффекте Комптона

λ – λ₀ = λ_C(1-cosθ) = 2λ_Csin²(θ/2)

λ₀ - длина волны падающего излучения, λ - длина волны рассеянного излучения, λ_C - комптоновская длина волны, θ - угол рассеяния.

λ_C =

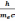
18. Сформулируйте корпускулярно-волновой дуализм

1) Почти монохроматическое излучение с частотой ω, испускаемое источником света, можно представить себе состоящим из «пакетов излучения», которые мы называем фотонами.

2) Распространение фотонов в пространстве правильно описывается классическими уравнениями Максвелла, при этом каждый фотон считается

классическим цугом волн, определённым двумя векторными полями E(r,t) и B(r,t).

3). Неправильно интерпретировать сумму квадратов амплитуд E и B как плотность энергии в пространстве, в котором движется фотон; вместо этого каждую величину, квадратично зависящую от амплитуды волны, следует интерпретировать как величину, пропорциональную вероятности какого-либо процесса.

4). Энергия, переданная в каком-либо месте пространства фотоном, всегда равна ħω. Тем самым

где W — вероятность нахождения фотона в данной области, а N — число фотонов.

19. Запишите выражение для спектрального терма водородоподобного атома

где R — постоянная Ридберга, а зарядовое число Z ядра введено ради удобства. Целое число n называется главным квантовым числом.

20. Запишите выражение для спектрального терма щелочных металлов

T(n) =

21. Запишите формулу Ридберга

, где R=1,1·10⁷

22. Запишите выражение для длины волны в серии Бальмера

, при k>2, n=3,4,..

np → 2s, ns → 2p, nd → 2p – серия Бальмера

23. Сформулируйте 1-й постулат Бора (дайте определение и запишите формулу)

Электрон в атоме водорода движется по круговым стационарным орбитам с постоянной скоростью под действием кулоновской силы в соответствии со вторым законом Ньютона. Разрешенными являются только те орбиты, на которых момент импульса электрона кратен ħ – постоянная Планка.

m r = nħ, n= 1,2,3…

24. Сформулируйте 2-й постулат Бора (дайте определение и запишите формулу)

Вращаясь по стационарным орбитам, электрон в атоме не излучает и не поглощает энергию, а излучает или поглощает энергию при переходе с одной стационарной орбиты на другую. Энергия излучения: hυ = E_n – E_m.

Если Е_m < E_n - то поглощает; Е_m > E_n – то излучает.

25. Запишите условие квантования Бора

L_n = mυr = nħ, n = 1,2,3…

26. Сформулируйте гипотезу де Бройля

Каждой движущейся частице, обладающей энергией Е и импульсом р, можно сопоставить волновой процесс, частота которого υ = Е/h, λ = h/p

а) Классический случай : <<C,T<<E₀, где Т – кинетическая энергия частицы. Тогда

Р = m , T = p²/2m → P =

б) Если частица релятивистская: ~ С, Т ~ Е₀, где ~ - соизмерима, то

Р = m₀/(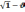 ²/C²)·

27. Запишите выражение для длины волны де Бройля нерелятивистской частицы

28. Запишите выражение для длины волны де Бройля релятивистской частицы

29. Запишите уравнение волны де Бройля

ψ(x,t)

ψ(x,t) = Ae^-i/h(ωt-kr)

30. Сформулируйте физический смысл ψ-функции

Физический смысл волновой функции: Квадрат модуля волновой функции дает плотность вероятности обнаружить микрочастицу в данной точке пространства в данный момент времени.

ρ = |ψ|²

31. Сформулируйте основные свойства ψ-функции

1) Вероятностная интерпретация волновой функции |ψ(r)|² dV

2) Свойство непрерывности, однозначности и конечности ψ-функции

3) Условие нормировки ∫ψ² dV = 1

4) Ортогональность собственных функций

[E_n - E_m]

32. Сформулируйте условие нормировки для ψ-функции

Условие нормировки ∫ψ*ψ dV = 1

33. Запишите два соотношения неопределённостей Гейзенберга

Δx · Δp_x ≥ ħ – Произведение неопределенности координаты на неопределенность проекции соответствующего импульса не может быть меньше постоянной Планка с чертой.

ΔE · Δt ≥ ħ – Произведение неопределенности энергии микрочастицы на время пребывания микро частицы в данной квантовом соотношении не может быть меньше постоянной Планка с чертой.

34. Запишите уравнение Шрёдингера для частицы в одномерной потенциальной яме

ψ(x) =

35. Запишите уравнение Шрёдингера для частицы в трёхмерной потенциальной яме

ψ(x,y,z,t) = A·sin x·B·sin y·C·sin z·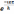

36. Запишите уравнение Шрёдингера для одномерного осциллятора

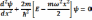
37. Запишите уравнение Шрёдингера для трёхмерного осциллятора

38. Запишите уравнение Шрёдингера для электрона в водородоподобном атоме

39. Сформулируйте принцип суперпозиции для квантовых состояний

ψ = a₁ψ₁ + a₂ψ_{2 ,} вероятность: |а₁|²,|а₂|²

40. Дайте определение вырожденных уровней энергии

Три разных квантовых состояний имеют одинаковые значения энергии. Состояния разные с одинаковыми значениями энергии называются вырожденными.

41. Дайте определение кратности вырождения энергетического уровня

Число состояний с одинаковым значением энергии называют кратностью вырождения.

42. Дайте определение туннельного эффекта

Туннельный эффект – квантовая микрочастица может выйти за пределы параболической ямы.

43. Сформулируйте физический смысл нулевой энергии квантового осциллятора

Покажем, что значение нулевой энергии   есть как раз то минимальное значение энергии осциллятора, которое согласуется с требованиями соотношения неопределенностей.

44. Укажите значения главного квантового числа

n = 1,2,3… - главное квантовое число.

45. Укажите значения орбитального квантового числа

Орбитальное квантовое число определяет момент импульса электрона в атоме:

l = 0,1,2,…,(n-1)

46. Укажите значения магнитного (орбитального) квантового числа

Магнитное орбитальное квантовое число m_l = 0,±1,±2,…±l, определяет проекцию момента импульса на физически выработанное направление.

47. Запишите возможные значения спинового квантового числа для электрона

L_s = ħ , s - спиновое квантовое число.

2s+1=2 → s = ½

48. Запишите возможные значения магнитного спинового квантового числа для электрона

L_sz = ħm_s, m_s - спиновое магнитное квантовое число. m_s = ±1/2

49. Запишите возможные значения квантового числа полного момента импульса электрона

50. Запишите выражение для квантованных значений энергии электрона в атоме водорода

E_n = -

51. Запишите выражение для квантованных значений орбитального момента импульса

L = ħ

52. Запишите выражение для квантованных значений проекции орбитального момента импульса на выделенную ось

53. Запишите выражение для квантованных значений спина

L_s = ħ

54. Запишите выражение для квантованных значений проекции спина на выделенную ось

55. Запишите выражение для квантованных значений полного момента импульса

56. Запишите выражение для квантованных значений проекции полного момента импульса на выделенную ось

57. Укажите значения спинового квантового числа для фермионов

58. Укажите значения спинового квантового числа для бозонов

59. Сформулируйте принцип Паули

Принцип Паули: В каждом квантовом состоянии, определяемом набором 4-х квантовых чисел n, l, m_l, m_s, не может быть более одного электрона.

60. Расшифруйте обозначение s-, p-, d-, f-, g- и h-состояний

резкая серия (sharp): nS

главная серия (principal): nP

диффузная серия (diffuse): nD

основная серия (fundamental): nF

II. СТАТИСТИЧЕСКАЯ ФИЗИКА И ТЕРМОДИНАМИКА

1. Дайте статистическое определение энтропии для неквазистатических процессов

2. Запишите распределение Максвелла

Распределение энергии Максвелла может быть выражено как дискретное распределение энергии:

, где является числом молекул имеющих энергию при температуре системы , является общим числом молекул в системе и — постоянная Больцмана. (Отметьте, что иногда вышеупомянутое уравнение записывается с множителем , обозначающим степень вырождения энергетических уровней)

Распределение по вектору импульса

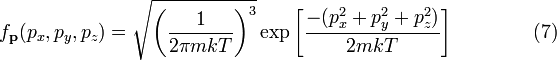.Распределение по вектору скорости

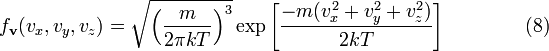
Распределение по абсолютной величине импульса

Интегрируя, мы можем найти распределение по абсолютной величине импульса

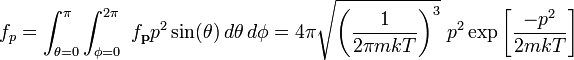
Распределение по энергии

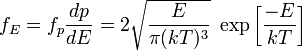
Распределение по проекции скорости

,

где распределение по одному направлению:

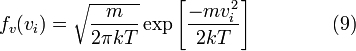
Распределение по модулю скоростей

,

где Таким образом, функция плотности вероятности для модуля скорости равна