
- •Принцип суперпозиции
- •20. Какие электромагнитные волны возможны в однородной изотропной среде? Продольные, поперечные или оба типа волн?
- •Определения и законы. Оптика (50)
- •Уравнения Максвелла (20)
- •Запишите выражения для потоков магнитного и электрического полей и сформулируйте их физический смысл (два уравненияия Максвелла).
- •Квантовая физика
- •Запишите распределение Больцмана
- •Запишите соотношение между средней скоростью, среднеквадратичной и наиболее вероятной скоростью. Покажите их на графике распределения Максвелла. Наиболее вероятная скорость
- •Средняя скорость
- •Среднеквадратичная скорость
Магнетизм
Определения (единица измерения)
Магнитная индукция – вектор, направление которого определяется равновесным направлением положительной нормали к пробному контуру. Теслы (Тл)
Магни́тный пото́к — поток
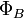 как
интеграл вектора магнитной
индукции
как
интеграл вектора магнитной
индукции 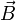 через
конечную поверхность
через
конечную поверхность 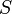 .
Определяется через интеграл по
поверхности
.
Определяется через интеграл по
поверхности
Вебер![]()
Потокосцепле́ние (полный магнитный поток) — физическая величина, представляющая собой суммарный магнитный поток, сцепляющийся со всеми витками катушки индуктивности. Вебер
4.
Магнитный
диполь
- аналог
электрического, который можно представить
себе как систему двух «магнитных зарядов»
(эта аналогия условна, так как магнитных
зарядов, с точки зрения современной
электродинамики,
не существует). В качестве модели
магнитного диполя можно рассматривать
небольшую (по сравнению с расстояниями,
на которых изучается генерируемое
диполем магнитное
поле)
плоскую замкнутую проводящую рамку
площади
![]() по
которой течёт ток
по
которой течёт ток
![]() При
этом магнитным моментом диполя (в системе
СГСМ)
называют величину
При
этом магнитным моментом диполя (в системе
СГСМ)
называют величину
![]() где
где
![]() —
единичный вектор, направленный
перпендикулярно плоскости рамки в том
направлении, при наблюдении в котором
ток в рамке представляется текущим по
часовой стрелке.
—
единичный вектор, направленный
перпендикулярно плоскости рамки в том
направлении, при наблюдении в котором
ток в рамке представляется текущим по
часовой стрелке.
5. Магнитный дипольный момент контура с током пропорционален произведению силы тока на площадь контура и направлен перпендикулярно плоскости контура так, что с его конца ток виден текущим против часовой стрелки. Дипольный момент определяет магнитное поле диполя на большом расстоянии от него, а также воздействие на диполь внешнего магнитного поля.
6. Явление электромагнитной индукции – во всяком замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток.
7. Явление самоиндукции. Электрический ток i, текущий в любом контуре, создает пронизывающий этот контур магнитный поток F. При изменении i будет изменяться также F и, следовательно, в контуре будет индуцироваться ЭДС.
8. Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между силой тока и полным магнитным потоком. Гн
9. Статический коэффициент самоиндукции – это коэффициент пропорциональности между силой тока и полным магнитным потоком. Динамический коэффициент самоиндукции – это коэффициент пропорциональности между скоростью изменения силы тока и ЭДС самоиндукции.
10. Напряженность магнитного поля.
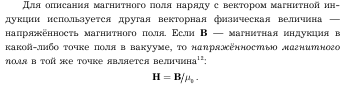 А/м
А/м
11. Вектор намагниченности – векторная физическая величина, равная сумме магнитных моментов (токов и микротоков) в единице объема вещества.
12. Магнитная проницаемость показывает во сколько раз индукция магнитного поля в веществе больше чем в вакууме. Магнитная восприимчивость – коэффициент пропорциональности между намагниченностью и напряженностью.
13.
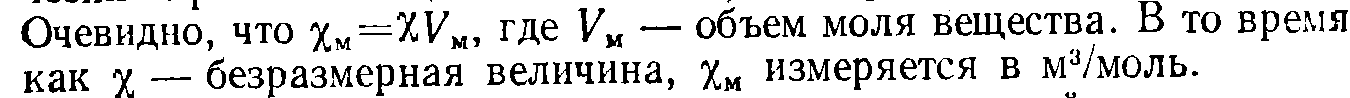
Χ-магнитная восприимчивость
![]()
Диамагнетики – это вещества, у которых в отсутствие внешнего магнитного поля магнитные моменты атомов равны нулю и, следовательно, намагниченность также равна нулю. χ< 0, 0<µ<0
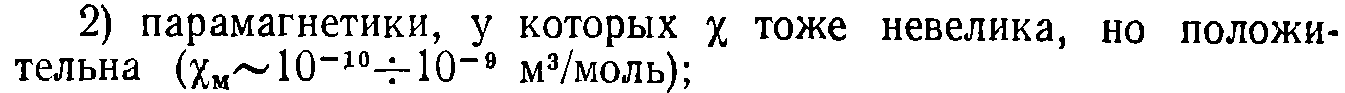
Парамагнетики – это вещества, у которых в отсутствие внешнего магнитного поля атомы обладают магнитным моментом, но эти магнитные моменты, вследствие теплового движения, направлены хаотично, поэтому в отсутствие внешнего магнитного поля намагниченность парамагнетиков равна нулю. χ>0, µ>1
![]()
![]()
Ферромагнетики – это вещества с недостроенными 3d оболочками(железо, кобальт) и 4f оболочками(тербий, диспрозий)
14.Токи Фуко – это вихревые замкнутые электрические токи в массивном проводнике, которые возникают при изменении пронизывающего его магнитного потока.
15. Токи проводимости - это такой ток, который обусловлен колебаниями электронов и ионов в среде(создаются движущимися зарядами)
16. Ток смещения – это ток, который обусловлен смещением электрических зарядов на границе «проводник – диэлектрик» (например, ток через конденсатор). (создается изменением напряженности электрического поля)
Формулы и законы
1-2


Принцип суперпозиции
Сила Ампера. Сила
 ,
с которой магнитное поле действует на
элемент
,
с которой магнитное поле действует на
элемент 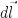 проводника
с током, находящегося в магнитном поле,
прямо пропорциональна силе тока
проводника
с током, находящегося в магнитном поле,
прямо пропорциональна силе тока 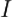 в
проводнике и векторному
произведению элемента
длины
в
проводнике и векторному
произведению элемента
длины  проводника
на магнитную индукцию
проводника
на магнитную индукцию 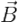 :
:

Правило левой руки. Если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции входила в ладонь, а 4 вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующий на проводник с током.
Сила Лоренца. Сила F действующая на частицу с электрическим зарядом q, движущуюся с постоянной скоростью v, во внешнем электрическом Eи магнитном B полях, такова:

Энергия магнитного диполя во внешнем поле.
Данное явление состоит в том, что при пересечении проводником линии магнитной индукции в проводнике индуцируются сторонние силы (ЭДС), что для замкнутого контура приводит к возникновению индукционного тока. В разомкнутом проводнике на его концах появляется разность потенциалов.
Вращательный момент действующий на магнитный диполь во внешнем поле.
При изменении тока, текущего по контуру изменяется магнитный поток через поверхность, ограниченную этим контуром, созданный этим током. Соответственно в контуре возникает ЭДС индукции, которое получило название самоиндукции.
Закон Фарадея для электромагнитной индукции (для ЭДС индукции).
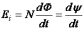 ,
где
,
где 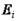 – эдс индукции;
– эдс индукции;  –
полный магнитный поток (потокосцепление).
–
полный магнитный поток (потокосцепление).Закон Фарадея для электромагнитной индукции (для заряда, прошедшего через контур).

Закон самоиндукции –

Правило Ленца

Теорема о циркуляции вектора магнитной индукции.
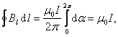 циркуляция
вектора магнитной индукции равна току,
охваченному контуром, умноженному
на магнитную постоянную.
циркуляция
вектора магнитной индукции равна току,
охваченному контуром, умноженному
на магнитную постоянную.
Индукция на оси соленоида бесконечной длины.

Индуктивность тороида, длинной катушки. B= μ0μIn /2πR, где N - число витков в тороидальной катушке, R - радиус окружности, проведенной внутри тороида вокруг его оси АА
Граничные условия для векторов B и H.
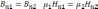
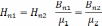
Работа и энергия магнитного поля.
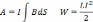
Объёмная плотность энергии магнитного поля

Колебания, оптика
Единица измерения (35)
1. Координаты частицы -
2. Сила - Ньютон (Н)
3. Скорость частицы – м/c
4. Энергия - Джоуль (Дж)
5. Угловая скорость - Радиан/секунда (рад/с)
6. Момент силы - Ньютон*метр (Н*м)
7. Ускорение частицы - м/с²
8. Угловое ускорение - рад*с−2
9. Мощность - Ватт (Вт)
10. Напряженность электрического поля - Вольт/метр (В/м)
11. Электрический заряд - Кулон (Кл)
12. Сила тока - Ампер (А)
13. Напряженность магнитного поля - Ампер/метр (А/м)
14. Напряжение - Вольт (В)
15. Активное сопротивление - Ом ?
16. Вектор магнитной индукции - Теслы (Тл)
17. Электроемкость - Фарада (Ф)
18. Индуктивность - Генри (Гн)
19. Вектор электрического смещения - Кл/м²
20. Частота - Герц (Гц)
21. Добротность колебательного контура -
22. Период колебаний - Секунда (с)
23. Фаза колебаний - Радиан (рад)
24. Коэффициент затухания - Непер (Нп) ?
25. Циклическая частота - Рад/с
26. Время релаксации - c
27. Логарифмический декремент затухания - дециБел
28. Импеданс контура - Ом
29. Волновое число - м−1
30. Плотность потока энергии - Вт/м2
31.Период дифракционной решетки - м
32. Поток энергии - Ватт
33. Реактанс контура - рад*м
34. Волновой вектор - м⁻¹
35. Вектор Пойтинга - Вт/м2
Формулы и выражения. Колебания (30)
1. Запишите выражение для периода колебаний математического маятника
T
= 2π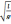
2. Запишите выражение для периода колебаний физического маятника
T
= 2π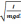
3. Запишите выражение для частоты колебаний математического маятника
ω =
4. Запишите выражение для частоты колебаний физического маятника
ω
= 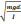
5. Запишите выражение для периода колебаний колебательного LC-контура
T=2π (называется
формулой Томсон)
(называется
формулой Томсон)
6. Запишите выражение для частоты колебаний колебательного LC-контура
ω0=
7. Запишите выражение для периода колебаний груза на пружине
T
= 2π
8. Запишите выражение для частоты колебаний груза на пружине
ω
= 
9. Запишите выражение для квазиупругой силы
Fξ
= - 
F=- kξ, где ξ— обобщённая координата, описывающая отклонение систе-
мы от положения равновесия.
10. Запишите выражение для кинетической энергии гармонического осциллятора


11. Запишите выражение для потенциальной энергии гармонического осциллятора
Wп=kx2/2
12. Запишите выражение для энергии электрического поля в LC-контуре
Wэ.п.
=  =
= 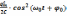
13. Запишите выражение для энергии магнитного поля в LC-контуре
Wм.п.
=  =
= 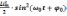
14. Запишите выражение для логарифмического декремента затухания через коэффициент затухания
λ=ln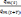 =ln
=ln =ln
=ln =βT=
=βT= =
=
где Ne — число совершённых колебаний за время затухания
15. Запишите выражение для коэффициента затухания RLC-контура
β
= 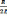
16. Запишите выражение для частоты колебаний в RLC-контуре
ω
= 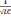
17. Запишите выражение для периода колебаний в RLC-контуре
T
= 2π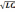
18. Запишите выражение для импеданса RLC-контура

Запишите выражение для импеданса RL-контура
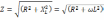
20.
Запишите выражение для импеданса
RC-контура
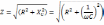
21. Запишите выражение для частоты биений выраженной через частоты складываемых колебаний
ωб
= 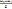 = 2(
= 2(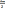 )
)
Запишите выражение для мощности в RLC-контуре.
23. Запишите уравнение свободных затухающих колебаний.

24. Запишите уравнение свободных незатухающих колебаний
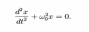
25. Запишите уравнение свободных затухающих колебаний

26. Запишите выражение для амплитуды колебания являющегося суммой двух сонаправленных колебаний одинаковых частот через амплитуды этих колебаний.
x=x1+x2
27. Запишите выражение для начальной фазы колебания, являющегося суммой двух сонаправленных колебаний одинаковых частот через амплитуды и начальные фазы этих колебаний.
Xm cos(ω1t+фи0)+Xm cos(ω2t+фи0)
28. Запишите дифференциальное уравнение свободных незатухающих колебаний.

Введем обозначение (частота собственных незатухающих колебаний или собственная частота), окончательно получим
|
- это дифференциальное уравнение свободных гармонических незатухающих колебаний.
29. Запишите дифференциальное уравнение свободных затухающих колебаний.
Дифференциальное
уравнение свободных затухающих колебаний
линейной
системы определяется как
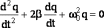 (1) где s – колеблющаяся величина, которая
описывает тот или иной физический
процесс, δ = const — коэффициент
затухания,
ω0
- циклическая частота свободных
незатухающих колебаний той же
колебательной системы, т. е. при δ=0 (при
отсутствии потерь энергии) называется
собственной
частотой
колебательной системы. b =
(1) где s – колеблющаяся величина, которая
описывает тот или иной физический
процесс, δ = const — коэффициент
затухания,
ω0
- циклическая частота свободных
незатухающих колебаний той же
колебательной системы, т. е. при δ=0 (при
отсутствии потерь энергии) называется
собственной
частотой
колебательной системы. b =
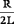 -
коэффициент затухания.
-
коэффициент затухания.
Его
решение q(t) = qv0
е-bt
cos(wt
+ a), где
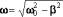 -
частота затухающих колебаний..
-
частота затухающих колебаний..
30. Запишите дифференциальное уравнение вынужденных колебаний.
 +2β
+2β +
+ =X(t)
=X(t)
β=
 =
= ,
x(t)=
,
x(t)=
Формулы и выражения. Волны (10)
1. Запишите уравнение плоской волны, распространяющейся вдоль оси Ох.
S = Acos(ωt – kx +φ0)
2. Запишите уравнение плоской волны, распространяющейся в произвольном направлении.
S(t,r) = Acos(ωt – kxx – kyy – kzz + φ0)
S(t,r) = Acos(ωt – kr + φ0) , kr – скалярное произведение.
3. Запишите уравнение сферической волны.
S(t,r,Θ,φ)
=  cos(ωt
± kr + φ0)
cos(ωt
± kr + φ0)
4. Запишите выражение для волнового числа.
k
= 
5. Запишите выражение для волнового вектора.
 где
где  -
постоянные амплитуда и фаза волны,
-
постоянные амплитуда и фаза волны, 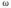 -
круговая частота, r -
радиус-вектор.
-
круговая частота, r -
радиус-вектор.
6. Запишите волновое уравнение.
S = Acos(ωt – kx)
7. Запишите выражение для скорости распространения упругих волн (через характеристики среды).
8. Запишите выражение для вектора Умова упругой волны.
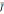 =w
=w где v — вектор скорости, нормальный к
волновой поверхности в данном месте,
w-
энергия
упругой волны
где v — вектор скорости, нормальный к
волновой поверхности в данном месте,
w-
энергия
упругой волны
9. Запишите уравнение затухающей волны.

10. Запишите уравнение стоячей волны.
S = Bcos(kx + ψ0)cos(ωt + φ0)
Формулы и выражения. Оптика (20)
Запишите выражение для показателя преломления через параметры среды.
Показа́тель
преломле́ния
вещества — величина, равная отношению
фазовых
скоростей света
(электромагнитных
волн) в вакууме
и в данной среде
![]() .
.
Запишите выражение для оптической длины пути.
Оптическая
длина пути
есть
![]() ,
где dl
- бесконечно малый элемент траектории
луча.
,
где dl
- бесконечно малый элемент траектории
луча.
Запишите выражение для показателя преломления через скорость световой волны в данной среде.
![]()
Запишите выражение для скорости световой волны через параметры среды, в которой он распространяется.
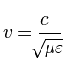
Запишите волновое уравнение для вектора напряжённости электрического поля.
![]()
Запишите волновое уравнение для вектора напряжённости магнитного поля.
![]()
Запишите выражение, связывающее амплитуды напряжённостей электрического и магнитного полей.
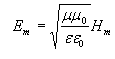
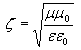
![]() ,
,
![]() .
.
Запишите выражение для вектора Пойтинга через характеристики электромагнитного поля.
![]() (в
системе СИ)
(в
системе СИ)
В этом соотношении проявляется материальность электромагнитного поля.
Запишите выражение для интенсивности света через амплитуду световой волны.
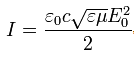
Запишите условие максимумов для фаз.
![]()
Запишите условие максимумов для оптической разности хода.
![]()
Запишите условие минимумов для фаз.
Запишите условие минимумов для оптической разности хода.
Запишите выражение для радиуса m-ой зоны Френеля.
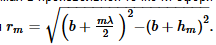
Запишите условие минимумов для дифракции Фраунгофера от щели.
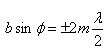
Запишите условие главных минимумов для дифракционной решётки.
![]()
Запишите условие дополнительных минимумов для дифракционной решётки.
![]()
Запишите условие главных максимумов для дифракционной решётки.
d·sinm ·
В формуле (3): d - период решетки, - угол отклонения лучей дифракции, - длина волны света, m - порядок дифракционного максимума
Запишите выражение для степени поляризации частично поляризованного света.
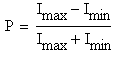
Запишите закон Бугера.
Интенсивность света при прохождении через вещество убывает по экспоненциальному закону:
![]() .
.
Определения и законы. Волны (20)
Дайте определение волн.
Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной)
Дайте определение продольной волны.
В продольных волнах частицы среды колеблются в направлении распространения волны.
Дайте определение поперечной волны.
в поперечных волнах частицы колеблются в плоскостях, перпендикулярных направлению распространения волны.
Дайте определение длины волны.
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны.
Дайте определение фазовой скорости волны.
скорость перемещения фазы волны называют фазовой скоростью.
Дайте определение фронта волны.
Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом.
Дайте определение волновой поверхности
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.
Дайте определение потока энергии.
Пото́к эне́ргии — это количество энергии, переносимое через некоторую произвольную площадку в единицу времени
Дайте определение плотности потока энергии.
Пло́тность пото́ка эне́ргии — физическая величина, численно равная потоку энергии через единичную площадку, перпендикулярную направлению потока.
Дайте определение когерентных волн.
Волны являются когерентными, если разность их фаз остается постоянной во времени. Очевидно, что когерентными могут быть лишь волны, имеющие одинаковую частоту.
Дайте определение принципа Гюйгенса.
Принцип Гюйгенса: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени.
Дайте определение стоячих волн.
Стоячие волны — это волны,образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами, а в случае поперечных волн еще и одинаковой поляризацией.
Дайте определение пучностей стоячей волны.
Точки, в которых амплитуда колебаний максимальна, называются пучностями стоячей волны.
Дайте определение узлов стоячей волны.
Точки, в которых амплитуда колебаний равна нулю, называются узлами стоячей волны.
Дайте определение волнового числа.
ВОЛНОВОЕ
ЧИСЛО -
модуль волнового
вектора; определяет
пространственный период волны (длину
волны ![]() )
в направлении её распространения:
)
в направлении её распространения:
![]()
Дайте определение волнового вектора.
ВОЛНОВОЙ ВЕКТОР - вектор k, определяющий направление распространения и пространственный период плоской монохроматической волны
Какие механические волны возможны в жидкой среде? Продольные, поперечные или оба типа волн?
Также к вопросам 18 и 19:
Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. в твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т.е. в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах — как продольные, так и поперечные.

