
- •1.Термодинамика и ее метод исследования.
- •2.Параметры термодинамической системы. Температура.
- •3.Параметры термодинамической системы. Давление.
- •4.Параметры термодинамической системы. Удельный объем.
- •6.Внутренняя энергия системы.
- •7.Энтальпия.
- •8.Понятие термодинамического процесса и термодинамическое равновесие.
- •9.Работа. Свойства p-V диаграмм.
- •10.Теплота.Свойства t-s диаграмм.
- •11.Первый закон термодинамики для замкнутого пространства.
- •12.Второй закон термодинамики. Обратимые и необратимые процессы.
- •13.Идеальный газ. Уравнение Клапейрона-Менделеева.
- •14. Газовая постоянная. Универсальная газовая постоянная.
- •15.Реальные газы. Уравнение состояния реальных газов.
- •16.Смеси идеальных газов и их свойства. Определение состава смеси.
- •17.Закон Дальтoна. Парциальное давление.
- •18.Газовая постоянная и средняя молярная масса смеси.
- •19.Понятия и определения теплоемкости.
- •20.Теплоемкость смеси идеальных газов.
- •21.Изотермический процесс.
- •22.Изобарный процесс.
- •23.Изохорный процесс.
- •24.Адиабатный процесс.
- •25.Политpoпные процессы.
- •27. Уравнение неразрывности потока
- •28. Связь между параметрами и функциями состояния в адиабатном потоке
- •29. Сопло и диффузор. Комбинированное сопло Лаваля.
- •31.Понятие о тепловых машинах. Холодильные машины и тепловые двигатели
- •32. Цикл Карно и его кпд
- •33 Циклы двс с подводом теплоты при постоянном объеме
- •34 Циклы двс с подводом теплоты при постоянном давлении
- •35.Цикл двс со смешанным подводом теплоты
- •36 Сравнительный анализ циклов поршневых двс.
- •37. Тепловой поток. Температурное поле. Градиент температуры.
- •38. Основные процессы теплопереноса. Теплопроводность.
- •39. Основные процессы теплопереноса. Конвекция.
- •40. Основные процессы теплопереноса. Тепловое излучение.
- •41. Дифференциальные уравнения процесса теплообмена.
- •48. Теплопроводность при граничных условиях III рода. Многослойная плоская стенка
- •49 . Теплопроводность при граничных условиях III рода. Цилиндрическая стенка.
- •51.Критерии гидродинамического подобия, критерии Фруда, Эйлера, Рейнольдса.
- •53. Вынужденная конвекция. Число Рейнольдса. Режимы течения.
- •54. Свободная конвекция. Число Грасгофа.
- •55 . Критерий подобия поля температур и скоростей. Число Прандтля.
- •56 Определяющие и определяемый критерии.
- •58. Теплообмен при вынужденном движении жидкости вдоль плоской стенки
- •59.Теплообмен при вынужденном движении жидкости вдоль
- •60 Теплообмен при поперечном обтекании пучка труб
40. Основные процессы теплопереноса. Тепловое излучение.
Тепловое
излучение-
это процесс переноса теплоты виде
электромагнитных волн. На поверхности
тела его внутренняя энергия превращается
в энергию электромагнитных волн различной
длины и распространяются со скоростью
света и волны. Теплообменное излучение
описывается законом Стефана Больцмана: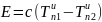 – плотность потока излучения E
– плотность потока излучения E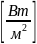 ,
с-приведенный коэффициент излучения
меду поверхностями с=
,
с-приведенный коэффициент излучения
меду поверхностями с=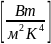 .
.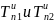 температура
принимаемого и излучаемого тел. Если
разность температур принимаемого и
излучаемого тел не велика, то расчет
теплообмена нужно вести в форме уравнения
Ньютона-Рихмана:
температура
принимаемого и излучаемого тел. Если
разность температур принимаемого и
излучаемого тел не велика, то расчет
теплообмена нужно вести в форме уравнения
Ньютона-Рихмана:
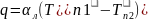 ,
где
,
где
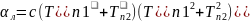 и
зависит от температуры и свойств тел,
участвующих в теплообмене излучения.
В общем случае теплообмен может
осуществляться тремя вышеперечисленными
методами. Процессы теплопроводности и
конвекции могут сопровождаться
теплообменным излучением.
и
зависит от температуры и свойств тел,
участвующих в теплообмене излучения.
В общем случае теплообмен может
осуществляться тремя вышеперечисленными
методами. Процессы теплопроводности и
конвекции могут сопровождаться
теплообменным излучением.
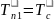 ,
,
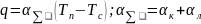 .
Процесс передачи от горячей текучей
среды холодной через разделяющую стенку
называется теплопередача.
.
Процесс передачи от горячей текучей
среды холодной через разделяющую стенку
называется теплопередача.
41. Дифференциальные уравнения процесса теплообмена.
Отношение
данных субстанций к объему обозначим
буквой Е. Для объема:
 ,
для массы:
,
для массы: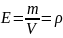 .
Для переноса количества движения
.
Для переноса количества движения
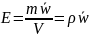 .
Полное изменение Е в объеме V
будет равно:
.
Полное изменение Е в объеме V
будет равно:
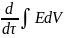 .
Часть субстанции переносится из объема
молекулярным путем. Поток субстанции
через поверхность F,
ограничивает данный объем, равен:
.
Часть субстанции переносится из объема
молекулярным путем. Поток субстанции
через поверхность F,
ограничивает данный объем, равен:
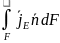 ,
где
,
где
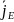 -плотность
потока, переносимая субстанцией,
-плотность
потока, переносимая субстанцией,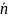 -
еденичный вектор нормали данной
поверхности.Используя формулу
Остроградского-Гауса:
-
еденичный вектор нормали данной
поверхности.Используя формулу
Остроградского-Гауса:
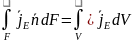 ;
Беря во внимание закон сохранения
субстанции можно сказать, что изменение
субстанции по времени будет равно:
;
Беря во внимание закон сохранения
субстанции можно сказать, что изменение
субстанции по времени будет равно:
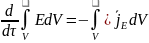 .
Считая подынтегральные функции
непрерывными можно записать:
.
Считая подынтегральные функции
непрерывными можно записать:
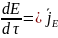
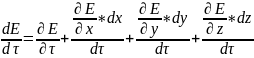 , где
, где
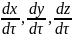 - Проекции скоростей,
- Проекции скоростей,
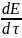 -
локальное изменение плотности субстанции.
-
локальное изменение плотности субстанции.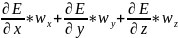 . Для процесса теплопроводности
. Для процесса теплопроводности
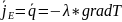 ,
поэтому можно записать, что
,
поэтому можно записать, что
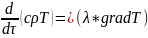 -
дифференциальное уравнение теплопроводности.
Фурье-Кирхгофа для неподвижного тела:
-
дифференциальное уравнение теплопроводности.
Фурье-Кирхгофа для неподвижного тела:
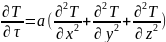 (1), a=
(1), a=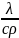 -температуропроводность
-температуропроводность ,
чем больше а, тем меньше тепловая
инерционность.Скорость изменения
температуры в любой точке тел, имеющих
большую тепловую инерционность, скорость
будет меньше, чем тел с малой тепловой
интенсивностью. Температуропроводность
зависит от состава, физического строения,
состояния и свойств тела.
,
чем больше а, тем меньше тепловая
инерционность.Скорость изменения
температуры в любой точке тел, имеющих
большую тепловую инерционность, скорость
будет меньше, чем тел с малой тепловой
интенсивностью. Температуропроводность
зависит от состава, физического строения,
состояния и свойств тела.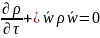 (2)- уравнение сплошности или неразрывности.
Для переноса количества движения и
предположения, что жидкость несжимаема
и
(2)- уравнение сплошности или неразрывности.
Для переноса количества движения и
предположения, что жидкость несжимаема
и
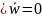 ,
можно получить следующее уравнение:
,
можно получить следующее уравнение: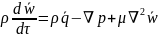 (3).
(3).
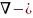 оператор
Гомельтона. Для описания теплообмена
в общем виде необходимо воспроизвести
систему диф. уравнений , состоящих из
трех приведенных (1),(2),(3).
оператор
Гомельтона. Для описания теплообмена
в общем виде необходимо воспроизвести
систему диф. уравнений , состоящих из
трех приведенных (1),(2),(3).
42. . Краевые условия теплоотдачи.
Чтобы
уравнение температурного поля отвечала
конкретному рассматриваемому случаю,
необходимо к дифференциальному уравнению
(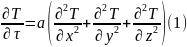 )
добавить условие однородности или
единственности решения. К данным условием
относятся геометрические и физические
характеристики тела, временные или
начальные условия и граничные условия.
Начальные и граничные условия в
совокупности называют краевыми условиями.
В качестве начальных условий принято
задавать распределение температур
внутри тела в начальный момент времени.
)
добавить условие однородности или
единственности решения. К данным условием
относятся геометрические и физические
характеристики тела, временные или
начальные условия и граничные условия.
Начальные и граничные условия в
совокупности называют краевыми условиями.
В качестве начальных условий принято
задавать распределение температур
внутри тела в начальный момент времени.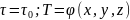 В самом простом случае:
В самом простом случае:
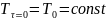 .
Граничные условия определяют особенности
взаимодействия изучаемого тела с
окружающей средой. Различают граничные
условия 1-го, 2-го, 3-го и 4-го рода. Граничные
условия 1-го рода задаются распределением
температур тела на поверхности в любой
момент времени. В частности для стац.
задачи принимается
.
Граничные условия определяют особенности
взаимодействия изучаемого тела с
окружающей средой. Различают граничные
условия 1-го, 2-го, 3-го и 4-го рода. Граничные
условия 1-го рода задаются распределением
температур тела на поверхности в любой
момент времени. В частности для стац.
задачи принимается
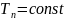 .
Граничные условия 2-го рода задаются
распределением плотности теплового
потока на поверхности тела в любой
момент времени
.
Граничные условия 2-го рода задаются
распределением плотности теплового
потока на поверхности тела в любой
момент времени
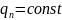 .
Граничные условия 3-го рода характеризуют
закон конвективного теплообмена между
поверхностью тела и окружающей средой
в соответствии с уравнением Ньютона-Рихмана.
Граничные условия 4-го рода- условие
сопряжения соотв. теплообмена
соприкасающихся тел, когда температура
тел в зоне контакта одинакова.
Дифференциальное уравнение(1) Фурье-Кирхгофа
вместе с краевыми условиями полностью
определяют задачу теплопроводности и
позволяет найти такую единичную функцию,
которая является решением конкретной
исследуемой задачи
.
Граничные условия 3-го рода характеризуют
закон конвективного теплообмена между
поверхностью тела и окружающей средой
в соответствии с уравнением Ньютона-Рихмана.
Граничные условия 4-го рода- условие
сопряжения соотв. теплообмена
соприкасающихся тел, когда температура
тел в зоне контакта одинакова.
Дифференциальное уравнение(1) Фурье-Кирхгофа
вместе с краевыми условиями полностью
определяют задачу теплопроводности и
позволяет найти такую единичную функцию,
которая является решением конкретной
исследуемой задачи
 .
.
43.Теплопроводность при граничных условиях 1 рода. Плоская стенка.
Д опускаем,
что материалы однородны и изотропны.
Коэффициент теплопроводности
опускаем,
что материалы однородны и изотропны.
Коэффициент теплопроводности
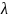 принимаем постоянным и исследуемый
режим- стационароным:
принимаем постоянным и исследуемый
режим- стационароным:
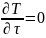 .
В качестве граничного условия 1-го рода
задается
.
В качестве граничного условия 1-го рода
задается
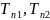 .
Целью решения задач является определение
изменения температур вдоль координаты
x.
.
Целью решения задач является определение
изменения температур вдоль координаты
x.
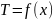 .
Плоская
стенка:
Полагаем, что длина и ширина стенки на
много больше ее толщины. Ось OX
направлена по нормали к поверхности
стенки.
.
Плоская
стенка:
Полагаем, что длина и ширина стенки на
много больше ее толщины. Ось OX
направлена по нормали к поверхности
стенки.
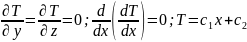 ,
где
,
где
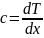 изменяется по линейному закону.
изменяется по линейному закону.
 определяются
из граничных условий
определяются
из граничных условий
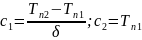 .
Зная
можно утверждать, что
.
Зная
можно утверждать, что
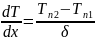 .Уравнение Фурье:
.Уравнение Фурье:
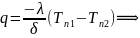 Плоскость
теплового насоса прямопропорциональна
перепаду температур на стенке и
обратнопропорциональна толщине стенки.
Общее количество теплоты, передаваемое
через поверхность за время
Плоскость
теплового насоса прямопропорциональна
перепаду температур на стенке и
обратнопропорциональна толщине стенки.
Общее количество теплоты, передаваемое
через поверхность за время
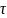 :
:
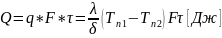 .
.
44. Теплопроводность при граничных условиях 1 рода. Многослойная плоская стенка.
Допускаем,
что материалы однородны и изотропны.
Коэффициент теплопроводности
принимаем постоянным и исследуемый
режим- стационароным:
.
В качестве граничного условия 1-го рода
задается
.
Целью решения задач является определение
изменения температур вдоль координаты
x.
.
Многослойная
плоская стенка: При
стационарном решении плотности теплового
потока, проходящие через каждую стенку,
если величина постоянная.
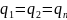
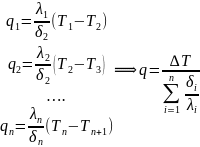
45. Теплопроводность при граничных условиях 1 рода. Цилиндрическая стенка.
Допускаем,
что материалы однородны и изотропны.
Коэффициент теплопроводности
принимаем постоянным и исследуемый
режим- стационароным:
.
В качестве граничного условия 1-го рода
задается
.
Целью решения задач является определение
изменения температур вдоль координаты
x.
.
Цилиндрическая
стенка: Температура
стенки будет изменятся только вдоль
радиуса.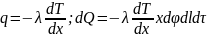 Учитывая, что
Учитывая, что
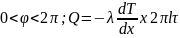
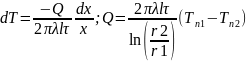 .
Для цилиндрической трубы используется
понятие теплового потока, отнесенного
к площади внутренней поверхности, к
наружной поверхности и к длине трубы.
.
Для цилиндрической трубы используется
понятие теплового потока, отнесенного
к площади внутренней поверхности, к
наружной поверхности и к длине трубы.
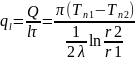 минимальное
термическое сопротивление цилиндрической
стенки.
минимальное
термическое сопротивление цилиндрической
стенки.
46. Теплопроводность при граничных условиях I рода. Шаровая стенка.

Шаровую стенку пронизывают тепловым
потоком:
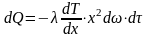 .
Учитывая, что
.
Учитывая, что
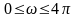 ,
то после интегрирования:
,
то после интегрирования:
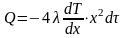 ;
;
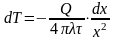 .
.
Учитывая,
что
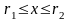 ,
а
,
а
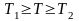 ,
мы можем получить:
,
мы можем получить:
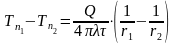
Откуда:
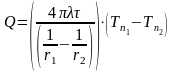 .
.
Откуда следует, что при стационарном режиме в шаровой стенке температура изменяется по гиперболе.
47. Теплопроводность при граничных условиях III рода. Плоская стенка.
Плоская стенка, толщиной δ и теплопроводностью материала λ, разделяет две среды с темп T1 и T2. Коэффициенты теплоотдачи со стороны среды 1 – α1. Считается, что T1, T2, α1, α2, λ – есть величины постоянные. Из этого следует: T=f(x).

Процесс стационарный:
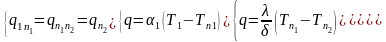
Складываем:
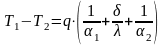
Выразим
q:
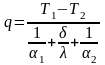 ;
;
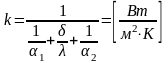
- коэф теплопередачи
Используя
k
, можно записать:
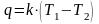 - ур-е теплопередачи.
- ур-е теплопередачи.
Величина 1/k наз полным термическим сопротивлением передачи.
