10. Логические модели. Исчисление предикатов. Пример.
Логика первого порядка (исчисление предикатов) — формальное исчисление, допускающее высказывания относительно переменных, фиксированных функций и предикатов. Расширяет логику высказываний. В свою очередь является частным случаем логики высшего порядка.
Язык логики
первого порядка строится
на основе сигнатуры,
состоящей из множества функциональных
символов 
и
множества предикатных символов 
.
С каждым функциональным и предикатным
символом связана арность,
то есть число возможных аргументов.
Допускаются как функциональные, так и
предикатные символы арности 0. Первые
иногда выделяют в отдельное
множество констант.
Кроме того, используются следующие
дополнительные символы
Символы переменных (обычно
и т. д.),Пропозициональные связки:
,Кванторы: всеобщности
и
существования 
,Служебные символы: скобки и запятая.
Перечисленные символы вместе с символами из и образуют Алфавит логики первого порядка. Более сложные конструкции определяются индуктивно:
Терм есть символ переменной, либо имеет вид
,
где 
—
функциональный символ арности 
,
а 
—
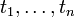термы.Атом имеет вид
,
где 
—
предикатный символ арности
,
а
—
термы.Формула — это либо атом, либо одна из следующих конструкций:
,
где 
—
формулы, а 
—
переменная.
Переменная
называется связанной в
формуле 
,
если
имеет
вид 
либо 
,
или же представима в одной из форм 
,
причем
уже
связанна в
, 
и 
.
Если
не
связанна в
,
ее называют свободной в
.
Формулу без свободных переменных
называют замкнутой
формулой,
или предложением. Теорией
первого порядка называют
любое множество предложений.
Свойства и основные результаты
Логика первого порядка обладает рядом полезных свойств, которые делают ее очень привлекательной в качестве основного инструмента формализации математики. Главными из них являютсяполнота (это означает, что для любой формулы выводима либо она сама, либо ее отрицание) и непротиворечивость (ни одна формула не может быть выведена одновременно со своим отрицанием). При этом если непротиворечивость более или менее очевидна, то полнота — нетривиальный результат, полученный Гёделем в 1930 году (теорема Гёделя о полноте). По сути теорема Гёделя устанавливает фундаментальную эквивалентность понятий доказуемости и общезначимости.
Логика первого порядка обладает свойством компактности: если некоторое множество формул не выполнимо, то невыполнимо также некоторое его конечное подмножество.
Согласно теореме Лёвенгейма — Скулема если множество формул имеет модель, то оно также имеет модель не более чем счетной мощности. С этой теоремой связан парадокс Скулема, который, однако, является лишь мнимым парадоксом.
[Править]Использование [править]Логика первого порядка как формальная модель рассуждений
Являясь формализованым аналогом обычной логики, логика первого порядка дает возможность строго рассуждать об истинности и ложности утверждений и об их взаимосвязи, в частности, о логическом следовании одного утверждения из другого, или, например, об их эквивалентности. Рассмотрим классический пример формализации утверждений естественного языка в логике первого порядка.
Возьмем рассуждение «Каждый человек смертен. Конфуций — человек. Следовательно, Конфуций смертен». Обозначим «x есть человек» через ЧЕЛОВЕК(x) и «x смертен» через СМЕРТЕН(x). Тогда утверждение «каждый человек смертен» может быть представлено формулой: x(ЧЕЛОВЕК(x) → СМЕРТЕН(x)) утверждение «Конфуций — человек» формулой ЧЕЛОВЕК(Конфуций), и «Конфуций смертен» формулой СМЕРТЕН(Конфуций). Утверждение в целом теперь может быть записано формулой
(
x(ЧЕЛОВЕК(x)
→ СМЕРТЕН(x)) 
ЧЕЛОВЕК(Конфуций))
→ СМЕРТЕН(Конфуций)
11. НЕ-факторы знаний
Знания, извлеченные из экспертов, содержат различные виды НЕ-фкторов, в связи с чем соответствующие методы и процедуры получения знаний должны обеспечивать возожность извлечения и обработки не полностью известной инфорации.
В ходе использования комбинированного метода приобретения знаний (КМПЗ) для разработки нескольких прикладных ИЭС удалось накопить экспериментальный материал, связанный с построением БД для трех типов задач – диагностики, проектирования и планирования, позволивший разработать целый ряд подходов к выявлению и обработке высказываний эксперта о свойствах ПрО, содержащих элементы нечеткости, неопределенности, неточности, отдельных видов недоопределенности, а также неполноты.
Для рассмотрения подобных знаний сточки зрения процессов извлечения и структурирования удобно выделить 2 основные группы НЕ-факторов знаний:
НЕ-факторы, проявляющиеся в рассуждениях эксперта в эксплицитном виде
НЕ-факторы, выделить которые в процессе интервьюирования эксперта на основе КМПЗ не представляется возможным, т.к. для их выявления требуются специльные механизмы и подходы (н-р, интервьюирование нескольких экспертов). В связи с этим введен ряд определений :
Недостоверные знания – знания, которые содержат НЕ – факторы, проявляющиеся эксплицитно в рассуждениях эксперта (т.е. относящися к 1 группе). Проведенные теоретические исследования показали, что распространнеными НЕ-факторами, проявление которых было отмечено в знаниях, полученны от экспертов, являются нечеткость, неопределенность, неточность, недоопределенность.
Используя теоретико –множественный подход , т.е в терминах xϵF , где x – элемент некоторого множества F, введены следующие определения для каждого из них.
Неопределенность - это степень неуверенности, которую эксперт приписывает своим высказываниям, т.е. некоторый субъективный коэффициент неполной уверенности в высказывании xϵF, который в зависимости от метода, используемого для обработки этого коэффициента, может иметь вид и интервала уверенности.
Нечеткость есть свойство количественной оценки экспертом качественных понятий и отношений, которые он использует в своих рассуждениях , когда по количественной оценке элемента х невозможно однозначно сказать , принадлежит он множеству F или нет.
Неопределенность отличается от нечеткости тем, что коэффицент уверенности приписывается не к каждому элементу х некоторого множества (в случае нечеткости), а только к конкретному высказыванию. В случае вероятностной интерпретации функции принадлежности (ФП) неопределенность можно свести к нечеткости. Приобретение нечетких знаний является черезвычайно сложной задачей, т.к эксперты не в состоянии самостоятельно определить ФП множества F.
Неточность –это часто встречающийся НЕ-фактор, т.к эксперты в своих рассуждениях опрерирует параметрами, полученными при помощи кких-либо измерительных приборов, которые имеют относительную погрешность измерения. Отсюда возникают неточные значения измерительных величин.
Неполнота означает, что неизвестен либо элемент х, либо множество F.
В условиях приобретения знаний неполнота связана с тем, что эксперт не знает (не отметил) какого-либо факта, необходимого для решения задачи. Возможны следующие альтернативы преодоления неполноты: либо проведение нескольких сеансов приобретения знаний с одним экспертом и срвнение результатов, либо привлечение нескольких экспертов и корреляция их мнений, а также использование технологии извлечение знаний из БД .
Наибольший разброс мнений наблюдается при определении недоопределенности. 1 мнение: Недоопределенность является отдельным НЕ- фактором, который включет в себя как недоопределенность общих знаний, так и недоопределенность конкретных знаний. Другая часть авторов под недоопределенностью понимает совокупность трех вышеупомянутых НЕ –факторов.
Под недоопределенностью общих знаний понимается частичное отсутствие знаний проблемной/предметной области в целом.
Под недоопределенностью конкретных знаний понимается частичное отсутствие знаний об отдельных понятиях и отношениях проблемной/предметной области.
Другими словами, недоопределенность конкретных знаний проявляется тогда, когда на значение какой-либо величины накладываются ограничения, что обычно не вызывает затруднения у эксперта, поэтому недоопределенность конкретных знаний является ниболее легко и часто выявляемой в процессе приобретения знаний. Поскольку невозможно определить адекватность модели ПрО, которой обладает эксперт, реальному миру, то вопросы выявления недоопределенности общих знаний затруднены , в связи с чем под термином «недоопределенности» часто понимается только недоопределеннсть конкретных знаний.
Рыбина, стр. 79