31. Аннулятор подпространства и его свойства.

Определение 3. Аннулятором подпространства U пространства V называется подпространство

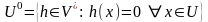
Теорема 2. dimU⁰ = dimV – dimU.

Д о к - в о. Пусть {e₁,e₂,…,e_n} – такой базис пространства V, что U= <e₁,e₂,…,e_k>, и {g₁,g₂,…,g_n} – сопряженный базис пространства V^*. Тогда U⁰ = <g_k+1,…,g_n>.

В соответствии с отождествлением пространств V^** и V, мы можем говорить об аннуляторе подпространства W пространства V^* как о подпространстве пространства V. По определению

Теорема 3. (U⁰)⁰ = U для любого подпространства U пространства V.

Д о к - в о. В обозначениях доказательства теоремы 2, ясно, что (U⁰)⁰ = <e₁,e₂,…,e_k> = U.

С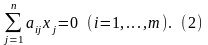 ледствие. Любое подпространство в V является аннулятором некоторого подпространства в V^*.

Пусть имеется система однородных линейных уравнений

Будем интерпретировать x₁,…, x_n как координаты вектора x n-мерного пространства V в некотором базисе {e₁,e₂,…,e_n} . Тогда система (2) может быть записана в виде h_i(x)=0 (i=1,…,m), где h₁,…,h_m – линейные функции, стоящие в левых частях уравнений (2).

Множество решений этой системы представляет собой аннулятор подпространства <h₁,…,h_m> пространства V^*. Заметим, что размерность этого подпространства равна рангу матрицы коэффициентов системы (2). Поэтому теорема о размерности подпространства решений системы однородных линейных уравнений является непосредственным следствием теоремы 2.

Следствие теоремы 3 может быть сформулировано так:

Теорема 4. Всякое подпространство в V является множеством решений некоторой системы однородных линейных уравнений.

32. Билинейные формы: определение и примеры. Матрица билинейной формы.

Определение 1.Билинейной формой (или билинейной функцией) на векторном пространстве V называется всякая функция h: V x V –> K, линейная по каждому аргументу.Пример 1.Как доказывается в курсе аналитической геометрии, скалярное умножение векторов является билинейной функцией на пространстве Е³.Пример 2. 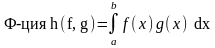явл. билинейной функцией на пр-ве C[a,b].Пример 3. Функция h(X,Y) = tr XY является билинейной функцией на пространстве L_n(K) квадратных матриц.Пример 4. Определитель матрицы второго порядка как функция ее строк есть билинейная ф-ция на пр-ве K². Пусть {e₁,e₂,…,e_n} – базис пр-ва V. Тогда для векторов x = x₁e₁ + x₂e₂ +…+ x_ne_n, y = y₁e₁ + y₂e₂ +…+ y_ne_n, получаем Матрица A=(a_ij) наз. матрицей билинейной функции h в базисе {e₁,e₂,…,e_n}. Как видно из предыдущей формулы, билинейная функция однозначно определяется своей матрицей.Формула (1) может быть переписана в матричных обозначениях: h(x,y)=X^ТAY, (2) где X и Y – столбцы векторов x и y соответственно. При переходе к другому базис (e₁^/,…,e_n^/) = (e₁,…,e_n) C координаты векторов x и y преобразуются по формулам X=CX^/, Y=CY^/_.. Подставляя эти выражения в (2), получаем h(x,y)=(X^/)^TC^TACY^/, откуда следует, что в базисе {e₁^/,…, e_n^/} матрица функции h равна C^TAC. Опр. 2. Ядром билинейной функции h называется подпространство Опр Билинейная функция h называется невырожденной, если Ker h = 0.Все билинейные функции, рассмотренные в примерах 1 – 4, невырожденны. Так, невырожденность скалярного умножения следует из того, что (у,у) > 0 при у, отличном от нуля. Аналогично доказывается невырожденность билинейной функции в примере 2. Если {e₁,e₂,…,e_n} – базис пространства V, то 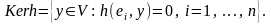Записывая эти условия в координатах, получаем систему однородных линейных уравнений, матрицей коэффициентов которой служит матрица A функции h. Следовательно, dim Ker h = n – rk A (3) В частности Ker h = 0, тогда и только тогда, когда rk A = n, т.е. когда матрица A невырожденна. Из формулы (3) следует, что ранг матрицы билинейной функции h не зависит от выбора базиса. Он называется рангом билинейной функции h и обозначается rk h. Опр 3. Билинейная функция h называется симметрической (соответственно кососимметрической), если h(x,y) = h(y,x) (соответственно h(x,y) = – h(y,x) ) для любых x, y из V. Билинейные функции в примерах 1 и 2 симметричны. Билинейная функция в примере 3 также симметрична. 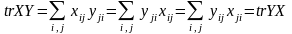В самом деле, если X = (x_ij), Y = (y_ij), то Билинейная функция в примере 4 кососимметрична. Но, конечно, существуют билинейные функции, которые не являются ни симметрическими, ни кососимметрическими. Билинейная функция является симметрической (соот. кососимметрической) тогда и только тогда когда ее матрица А симметрична (соответственно кососимметрична), т.е. А^Т = А (соответственно А^Т = – А).