10. Матрица перехода от одного базиса к другому. Формула преобразования координат при переходе к новому базису.

Матрица С наз. матрицей перехода от базиса {е_1, ..., е_п} к системе {е’_1, ..., е’_п} .

e'1=e1c11+…+encn1

…

e'n=e1c1n+…+encnn

e=(e1,…,en) строка e умножается на столбец матр.

e’=(e’1,…,e’n)

e’=e*C

Если строка матрицы ЛЗ, то ёё определитель равен 0.

Если определитель равен нулю, то строки матр. ЛЗ.

j-ый столбец матр. С есть столбец координат вектора e’j в базисе { e1,…,en }. Поэтому векторы e’1,…,e’n, ЛНЗ (и, значит, составляют базис) тогда и только тогда, когда столбцы матр. С ЛНЗ, т.е. когда матр. С невырожденна.

Следовательно, матрица перехода от одного базиса линейного пространства к другому базису того же линейного пространства невырожденна.

Если распространить правило умножения матриц на случай, когда элементами одной из них являются векторы (что имеет смысл ввиду операций, определенных в векторном пространстве), то равенства могут быть переписаны в следующей матричной форме (е’1,...,е'_п) = (е₁,...,е_п)С.

Пусть х— какой-либо вектор пространства V . Разложим его по базисам {е,,..., е„} и {е{,..., е'_п}:

x=x1e1+…+xnen=x’1e’1+…+x’ne’n.

X=(x1 X’=(x’1

… …

xn) x’n)

Тогда х = (е₁',...,еn); Х' = (е₁,...,е_n)СХ', откуда получается следующая формула преобразования координат при переходе от базиса {е1,..., еn} к базису {е’1,,..., е'_п}:

X = СХ'; (е₁',...,е’n)=(e’1,,..., е'_п)*X, т.к. координаты вектора X в базисе {е1,..., еn} определяется единственным образом.

Более подробно формулы X=C*X’ модно записать в виде

11. Ранг системы векторов. Ранг матрицы. Эквивалентные системы векторов.

С понятием размерности тесно связаны понятия ранга системы векторов и ранга матрицы.

Определение 4. Рангом системы векторов называется раз­мерность ее линейной оболочки. Рангом матрицы называется ранг системы ее строк.

Ранг матрицы А обозначается через rk А.

Системы векторов {а₁ ..., аn} и {b1,..., Ь_m} называются эквивалентными, если каждый из векторов линейно выражается через векторы {а₁, ..., а_п } и каждый из векторов а_i линейно выражается через векторы {b1,…,bm} .

Системы векторов <a₁,a₂,...,a_n> = <b₁,b₂,...,b_m> эквивалентны тогда и только тогда, когда линейные оболочки этих систем векторов совпадают, т.е. линейная оболочка натянутая на <a₁,a₂,...,a_n >= <b₁,b₂,...,b_m>. Пусть матрицы А', получена из матрицы А с помощью эквивалентных преобразований. Следовательно строки матрицы А' линейно выражается через строки матрицы А. Тогда и матрица А может быть получена из А' с помощью эквивалентных преобразований над строками того же типа, при этом строки матрицы А' линейно выражаются через строки А и наоборот. Следовательно, системы строк матриц А эквивалентна системы строк матриц А’, след., ранг A’ равен рангу А.

12. Вычисление ранга матрицы с помощью приведения её к ступенчатому виду.

Предложение 3. Ранг матрицы равен числу ненулевых строк любой ступенчатой матрицы, к которой она приводится эле­ментарными преобразованиями строк.

Доказательство. Так как ранг матрицы не меняется при элементарных преобразованиях, то нам достаточно доказать, что ранг ступенчатой матрицы равен числу ее ненулевых строк. Для этого, в свою очередь, достаточно доказать, что ненулевые строки ступенчатой матрицы линейно независимы.

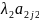Предположим, что линейная комбинация ненулевых строк сту­пенчатой матрицы с коэффициентами λ1,…, λr равна нулю. Рассматривая -ю координату этой линейной комбинации, находим, что λ1а_1;- =0, откуда λ1=0. Рассматривая, далее, j₂-ю координату с учетом того, что 1 =0, находим, что = 0, откуда λ ₂ = 0. Продолжая так дальше, получаем, что все коэффициенты λ1,…, λr равны нулю, что и требовалось доказать. □

Следствие. Какую бы последовательность элементарных преобразований, приводящую данную матрицу к ступенчатому виду, мы не выбрали, число ненулевых строк полученной ступенчатой матрицы будет всегда одним и тем же.