
- •Определение и примеры векторных пространств.
- •Подпространства линейного пространства: определения и примеры
- •Линейные комбинации векторов. Линейно зависимые и линейно независимые системы векторов и их св-ва.
- •Линейная оболочка множества. Конечномерные бесконечномерные векторные пространства
- •Основная лемма о линейной зависимости
- •Определение базиса линейного пространства. Переформулировка определения базиса. Теорема о существовании базиса в конечномерном векторном пространстве.
- •7. Размерность векторного пространства.
- •10. Матрица перехода от одного базиса к другому. Формула преобразования координат при переходе к новому базису.
- •11. Ранг системы векторов. Ранг матрицы. Эквивалентные системы векторов.
- •12. Вычисление ранга матрицы с помощью приведения её к ступенчатому виду.
- •13 Теорема Кронекера – Капелли.
- •14 Сумма и пересечение подпространств.
- •15 Базисы, согласованные с подпространствами. Теорема о базисе, согласованном с двумя подпространствами, со следствием.
- •16 Лнз системы подпространств и их свойства
- •17 Прямые суммы подпространств. Разложение линейного пространства матриц порядка с элементами из поля в прямую сумму двух подпространств)
- •25.Теорема об изоморфизме алгебры линейных операторов и алгебры матриц.
- •26.Подпространства, инвариантные относительно линейных операторов.
- •27.Собственные векторы и собственные значения ло.
- •28.Необходимые и достаточные условия существования базиса из собственных векторов линейного оператора.
- •29.Определение и примеры линейных форм.
- •30.Сопряжённые пространства и их свойства.
- •31. Аннулятор подпространства и его свойства.
- •32. Билинейные формы: определение и примеры. Матрица билинейной формы.
- •33. Квадратичные формы: определение и примеры. Матрица квадратичной формы.
- •34. Ортогональные подпространства и их свойства.
- •35. Процесс ортогонализации Грама-Шмидта.
- •36 Положительно определённые квадратичные формы. Критерий Сильвестра.
- •37. Закон инерции вещественных квадратичных форм
- •38. Метод Якоби
- •39. Метод Лагранжа
- •40. Евклидовы пространства: определение и примеры.
- •41. Неравенство Коши-Буняковского. Матрица Грамма и ее свойства.
- •42. Ортогональные матрицы и их свойства
- •43. Сопряженный оператор, его свойства
- •44. Самосопряжённые операторы, ортогональные операторы и их свойства
- •45. Приведение квадратичной формы к главным осям
- •46. Теорема о полярном разложении линейного оператора, действующего в евклидовом пространстве.
- •47. Корневые подпространства
- •48. Теорема о размерности корневого подпространства
- •49. Разложение линейного пространства в прямую сумму корневых подпространств.
- •50. Нильпотентные операторы и их свойства.
- •51. Разложение линейного пространства в прямую сумму циклических подпространств.
- •52. Жордановы матрицы.
- •53. Минимальный аннулирующий многочлен линейного оператора и его свойства.
42. Ортогональные матрицы и их свойства
Согласно общей теории, в любом конечномерном евклидовом пространстве существует ортонормированный базис. Такой базис, конечно, не единственен. Дадим описание всех ортонормированных базисов , исходя из какого-либо одного ортонормированного базиса { , … , }.
Пусть
(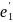 ,
… ,
,
… ,
 )=
(
)=
(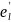 ,
… ,
)C.
Тогда матрица скалярного умножения в
базисе {
,
… ,
}
является ортонормированным тогда и
только тогда, когда
,
… ,
)C.
Тогда матрица скалярного умножения в
базисе {
,
… ,
}
является ортонормированным тогда и
только тогда, когда
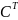 C=E.
очевидно, что следующие свойства матрицы
С эквивалентны:
C=E.
очевидно, что следующие свойства матрицы
С эквивалентны:
C=E;
 =
при всех I,j;
=
при всех I,j;=
 ;
;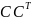 =Е;
=Е; =
при всех I,j.
=
при всех I,j.
Матрицы, обладающие этими эквивалентными свойствами, называются ортогональными.
Заметим, что из равенства C=E следует соотношение detC=±1 (но не наоборот!).
43. Сопряженный оператор, его свойства
Пусть А линейный оператор, действующий в пространстве Е со скалярным произведением (х,у).
Линейный оператор А*, соответствующий функции fAT , называется сопряженным оператором по отношению к А. Иначе говоря, сопряженный оператор определяется множеством (А* х, у)=(х, Ау)
Матрицей оператора А* в ортонормированном базисе является транспонированная матрица оператора А
Пусть В = (е1,…,еn) – какой-нибудь ортонормированный базис пространства Е. Поскольку равенство (А* х, у)=(х, Ау) верно для любых векторов, то оно верно и для векторов базиса: (Аеi, ej) = (ei, A*ej).
Свойства:
А** = А
Пусть х и у - произвольные векторы. Тогда
(Ах, у) = (х, А*у) = ( )
= (
)
= (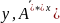 )
= (А**х, у)
)
= (А**х, у)
Т.к. это верно для
 у,
то Ах = А**х
у,
то Ах = А**х
Поскольку х – произвольный вектор, то А=А**.
(А+В)* = А* + В*.
((А+В)*х,у) = (х,(А+В)у) = (х,Ау+Ву) = (х,Ау)+(х,Ву) = (А*x,y)+(B*x,y) = (A*x+B*x,y) = ((A*+B*)х,у). Отсюда, в силу произвольности векторов х и у, получаем (А+В)* = А*+В*
(A,B)* = B*A*
A)* =
 A*
A*(A-1)*=(A*)-1, если А – невырожден.
44. Самосопряжённые операторы, ортогональные операторы и их свойства
Линейный оператор А в пространстве со скалярным произведением называется самосопряженным, если А = А*. Так же симметрические операторы называются самосопряженными.
Симметрическим (кососимметрическим) билинейным функциям соответствует так называемые симметрические (кососимметрические) линейные операторы. Они характеризуются тем, что А*=А (А*=-А), а в матричных терминах – тем, что их матрица в ортонормированном базисе симметрична(кососимметрична)
Линейные операторы, для которых А*=А-1, называются ортогональными. Иначе говоря, оператор А, ортогонален если (Ах, Ау) = (х,у)
(Ах, Ау) = (х,А*Ау) = (х,А-1Ау) = (х,у), т.е. если А сохраняет скалярное произведение векторов.
Из
тождества
(х,у)= (|x+y|2
- |x|2
- |y|2)
следует, что оператор А ортогонален
тогда и только тогда, когда он сохраняет
длины векторов.
(|x+y|2
- |x|2
- |y|2)
следует, что оператор А ортогонален
тогда и только тогда, когда он сохраняет
длины векторов.
(х,у) = (|x+y|2 - |x|2 - |y|2) = ((x+y, х+у) – (x, х) – (y,у)) = ((х,x+y) + (у,x) + (у,x) – (х, х) – (у,y)) = ((х,х)+(x,y) + (у,x) + (у,у) – (х, х) – (у,y)) = (х,у)
В матричных терминах ортогональные операторы характеризуются тем, что их матрица в ортонормированном базисе ортогональна.
Предложение 1.
Линейный оператор любого из рассматриваемых выше трех типов, т.е. симметрический, кососимметрический или ортогональный, обладает следующим свойством: если подпространство U инвариантно, то и его ортогональное дополнение U└ инвариантно.
Доказательство.
Рассмотрим
наиболее сложный случай ортогонального
оператора А.
Заметим, прежде всего, что оператор А|U
также
ортогонален и, следовательно, невырожден.
Поэтому для любого вектора х U
найдется такой вектор у
U└.
Тогда, используя предыдущие обозначения,
получаем для любого х
U
U
найдется такой вектор у
U└.
Тогда, используя предыдущие обозначения,
получаем для любого х
U
(х, Ау) = (Аz , Ay) = (z , y) = 0, откуда следует, что Ау U└.
