Вариант 1.

Задание1. ОПРЕДЕЛИТЕЛИ. Вычислить определители:

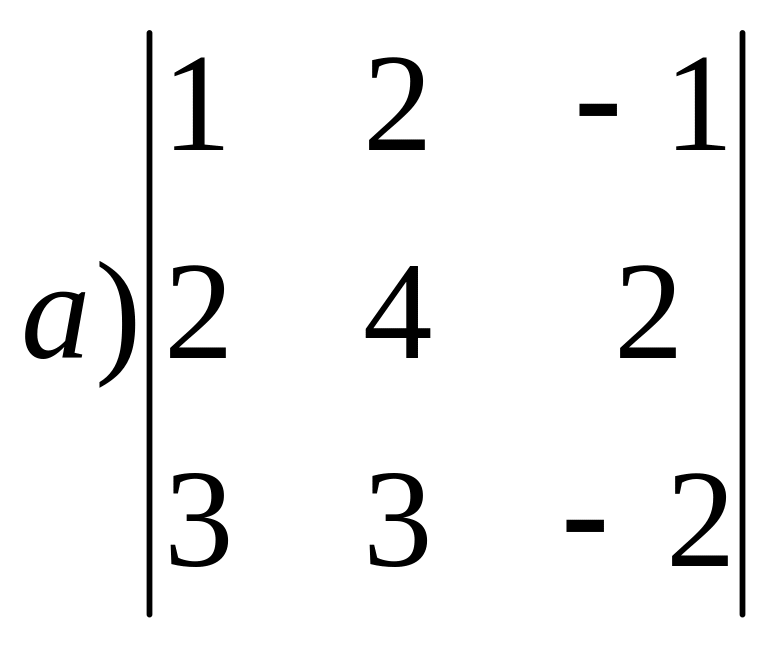
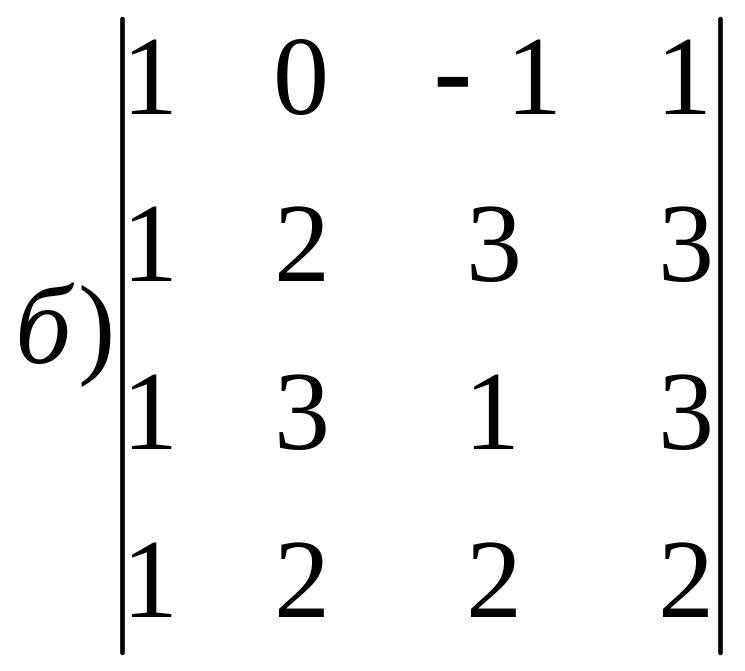
Задание 2. Системы уравнений.

1. Решить систему методом Крамера и проверить методом Гаусса.

2.Решить систему с помощью обратной матрицы. Сделать проверку.

Задание 3. Прямая на плоскости

В АВС даны координаты вершин: , ,

1.Построить чертеж. 2.Найти периметр треугольника.

3.Составить уравнения сторон треугольника. 4.Составить уравнение прямой ВN // АС.

5.Составить уравнение медианы СД. 6.Уравнение высоты АЕ, найти ее длину.

7.Найти углы треугольника. 8.Найти координаты центра тяжести.

Задание 4. ПРЯМАЯ И ПЛОСКОСТЬ. Даны координаты вершин пирамиды А А А А .

А (7; 7; 3), А (6; 5; 8), А (3; 5; 8), А (8; 4; 1). Найти:

1) длину ребра А А ; 2) угол между ребрами А А и А А ;3) уравнение прямой А А ;

4) площадь грани А А А ; 5) объем пирамиды; 6) уравнение плоскости А А А ;

7) угол между ребром А А и гранью А А А ; 8)уравнение высоты и ее длину, опущенной

из вершины А на грань А А А ; 9)сделать чертеж.

Задание 5. КРИВЫЕ ВТОРОГО ПОРЯДКА.

1.Найти координаты вершины и фокусов параболы, составить уравнения оси и директрисы параболы: а/ х²+6х+12у -27=0, б/ у²-2у -10х +21=0.

2. Построить кривые по данным уравнениям: а) (х +2) +(у +4) = 49

б) , в)

Задание 6. Предел функции.

6.1. Вычислить предел функции при х х : f(x) = а) х = 2; б) х = -2; в) х = .

6.2. Вычислить предел функции при х х : f(x) = х = 3.

6.3. Вычислить предел функции при х 0: f(x) =

6.4. Вычислить предел функции при х : f (x) =

Задание 7. Найти производные функций: а) у = , б) у = ,

в) у = sin 4x · 5 , г) y = ln arcsin 3x.

Задание 8. Применение производной.

а) Составить уравнения касательной и нормали к графику кривой у = 2х² - 5х -3, в точке, с абсциссой x₀ = 2 .

б) Найти максимальную скорость, если точка движется по закону S(t) = -1/3 t³+ 8t² - 8t – 5

в) Найти наибольшее и наименьшее значения функции f(x) = - x³ + 3x² + 2 на 1; 4

Задание 9. ИССЛЕДОВАНИЕ ФУНКЦИИ.

Исследовать данные функции методом дифференциального исчисления и построить их графики:

а) у = х - 3х² + 3 б) у =

Задание 10. Интегральное исчисление.

1.Найти неопределенный интеграл, проверить результат дифференцированием в заданиях а, б, в, г.

2. Вычислить неопределенный интеграл в заданиях д, е.

3.Вычислить определенный интеграл в задании ж.

а) б) в) г) dx

д) е) ж)

Задание 11. Площадь фигуры.

С помощью определенного интеграла вычислить площадь фигуры, ограниченной линиями. Сделать чертеж: а) х + 3у - 4= 0, х – 3у + 2 = 0, у = 0. б) у = х³ -2, у = х - 3, х = 0, х = 2.

Задание 12. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.

Вычислить приближенное значение определенного интеграла с помощью формулы Симпсона, разбив отрезок на 10 частей, с точностью до 0,001: dx