1. Фотоэффект.

П од фотоэффектом понимают изменение состояния электронов в веществе под действием света (эл.маг излучения). Различают внутренний и на внешний фотоэффекты. При внутреннем фотоэффекте электроны с поверхности вещества не вырываются. Внешний фотоэффект состоит в вырывании электронов с поверхности вещества под действием электромагнитного излучения Сущность внешнего фотоэффекта: Сквозь кварцевую пластинку на катод подал свет. При этом, при отсутствии внешнего напряжения, амперметр показывал некоторый небольшой ток. При включении внешнего напряжения, ток в цепи возрастал почти линейно до некоторого значения. После этого наступал эффект насыщения. В то же время, при нулевом напряжении, некоторый ток существовал. Прикладывая отрицательное напряжение, получим нулевой ток. Величина фототока зависит как от длины падающей волны, так и от интенсивности излучения. Вообще говоря, интенсивностью излучения называют энергию, проходящую за единицу времени через поверхность единичной площади. Зависимость напряжения от различной частоты падающего излучения, показана на рисунке 3а. Здесь ν₃< ν₁< ν₂, то есть с увеличением частоты, режим насыщения наступает при большем токе до какого-то определённого уровня. Потом дальнейший рост частоты уже не приводит к росту тока, а, наоборот, к его уменьшению. Качественно это показано на рисунке 3в. Зависимость фототока от интенсивности излучения приведена на рисунке 3б.

Рассмотрим его законы. Законы фотоэффекта.

1. Закон Столетова. Существует граничная частота , ниже которой для данного материала катода фотоэффект отсутствует независимо от плотности светового потока энергии и продолжительности облучения катода. Эта граничная частота называется красной границей Значение этой границы зависит только от рода атомов. Энергия, которую нужно затратить, чтобы вырвать электрон из вещества, называется работой выхода. .

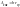2. Закон фотоэффекта. Максимальная энергия фотоэлектрона, покидающего катод, равна 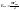; не зависит от плотности энергии светового потока и линейно зависит от частоты.

3. Закон фотоэффекта. При фиксированной частоте излучения число электронов, выбиваемых из катода в единицу времени, прямо пропорционально плотности светового потока энергии.

Обобщая законы фотоэффекта, Эйнштейн записал уравнение фотоэффекта: - энергия фотона, попадающего на катод, идёт на преодоление работы выхода электрона из материала катода и на сообщение ему кинетической энергии.

Дж·с.

Возвращаясь к различным видам фотоэффекта, необходимо заметить, что существует так называемый ядерный фотоэффект. Так называют явление поглощения сильно коротковолнового излучения (рентгеновского или – излучения) ядрами атомов, в результате которого происходит вылет нуклонов (протонов и нейтронов) из ядер.

2. Эффект Комптона.

Исследуя спектр, Комптон заметил, что лучи, рассеянные на угол меньше , обладают большей длиной волны, чем исходное излучение, так что частота вторичной волны оказывается вопреки классической теории меньше, чем частота первоначального электромагнитного поля. Причём, энергия рассеянных фотонов (а значит и их частота) зависит от угла рассеяния . Комптон сделал вывод, что сдвиг длины волны линейно пропорционален 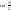, где – угол рассеяния. Таким образом, чтобы поставить знак равенства, необходимо умножить на некоторую константу. Мы можем записать: (1), где – комптоновская постоянная (комптоновская длина волны). Рассмотрим теперь графики зависимости для различных . Из графиков видно, что функция при различных имеет максимум не только при исходной длине волны, но и при некоторых других.

Для объяснения эффекта Комптона, Дебай рассмотрел упругое столкновение двух частиц: светового кванта и электрона.

П усть до взаимодействия электрон неподвижен. Фотон с импульсом взаимодействует с электроном мишени, рассеивается на нём. Импульс фотона изменяется и становится равным . Электрон также рассеивается и при этом получает импульс . Таким образом, мы можем записать законы сохранения импульса и энергии:

В формуле (3) под подразумевается масса покоя электрона. Проведём некоторые преобразования. Сложим импульс по правилу параллелограмма. Для треугольника применим теорему косинусов:

. Так как , то

(4).

И з равенства (3) следует, что или . Из последнего выражения найдём : 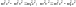. Подставим последнее выражение в формулу (4), и, учитывая закон сохранения энергии: (получается из формулы (3)), запишем:

. Разделим последнее выражение на :; . Так как , то . Преобразуя последнее выражение, получим: . Обозначим . Тогда . Отсюда или (5). В последней формуле выражение является постоянной, так как из таковых состоит. Вычисления показывают, что , что в точности совпадает с комптоновской постоянной. Таким образом, (5) можно переписать так , что в точности совпадает с опытной формулой (1). Из полученного соотношения следует, что квантовая теория хорошо объясняет эффект Комптона, исходя из корпускулярных свойств излучения.