30.Биномиальное распределение
Пусть выполнены все условия схемы независимых испытаний Бернулли.
Рассмотрим
в качестве ДСВ
число появлений события
в этих испытаниях. Т. е. величина
может принимать значения:
.
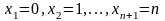Вероятности этих значений определяются по формуле Бернулли:
,
.
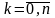О. 2. Закон распределения вероятностей ДСВ называется биномиальным, если вероятности ее возможных значений определяются по формуле Бернулли.
31. Пуассоновское распределение
Пусть
в схеме независимых испытаний Бернулли
число испытаний достаточно велико (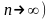
,
а вероятность появления события
очень мала
.
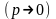Рассмотрим в качестве ДСВ число появлений события в этих испытаниях. Т. е. величина может принимать значения: .
Вероятности этих значений определяются по формуле Пуассона:
, .
О. 3. Закон распределения вероятностей ДСВ называется пуассоновским, если вероятности ее возможных значений определяются по формуле Пуассона.
32.Геометрическое распределение
Пусть
выполнены все условия схемы независимых
испытаний. Испытания проводятся до
1-го появления события
.
Т. е. если событие
появилось в
-м
(катом) испытании, то в предыдущих
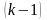испытаниях оно не появлялось.
Рассмотрим
в качестве ДСВ
число испытаний, которые необходимо
провести до 1-го появления события
.
Т. о. возможные значения величины
:
.
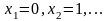Вероятности этих значений определяются по формуле:
,
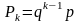где
.
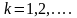(1)
Если
в эту формулу подставить последовательно
вместо
:
,
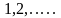то получим геометрическую прогрессию
с 1-м членом
и знаменателем
(
)
:
.
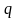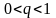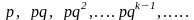O. 4. Закон распределения вероятностей ДСВ называется геометрическим, если вероятности ее возможных значений определяются по формуле (1) и образуют геометрическую прогрессию.
33.Гипергеометрическое распределение
Пусть
имеется
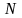элементов, среди которых
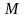обладают свойством
.
Случайным образом выбирается
элементов (выбор каждого элемента
равновозможен), причем выборка
осуществляется без возвращения.
Рассмотрим в качестве ДСВ количество элементов , обладающих свойством среди отобранных элементов. Т. е. величина может принимать значения: .
Вероятности этих значений определяются по формуле:
,
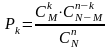где
.
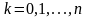(2)
O. 5. Закон распределения вероятностей ДСВ называется гипергеометрическим, если вероятности ее возможных значений определяются по формуле (2).
34.Равномерное распределение
О.1. Закон распределения НСВ называется равномерным, если ее плотность распределения задается в виде:
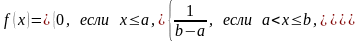
Свойства равномерного распределения
1. Зная плотность распределения, и используя формулу ,
можно найти функцию распределения:
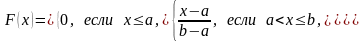
2. Если НСВ имеет равномерное распределение, то ее числовые характеристики могут быть найдены по формулам:
.
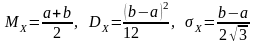3.
Вероятность попадания равномерно-распределенной
НСВ
в интервал
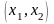можно определить по формуле:
.
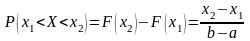