
- •3. Испытание. Событие. Классификация событий
- •4.Понятие вероятности события
- •5.Статистическое определение вероятности. Относительная частота события
- •6. Геометрическое определение вероятности.
- •7.Алгебра событий
- •9. Теоремы умножения вероятностей
- •10.Теоремы сложения вероятностей
- •11.Вероятность появления хотя бы одного события
- •12.Формула полной вероятности
- •13.Вероятность гипотез. Формула Байеса
- •15.Формула Бернулли
- •16. Локальная теорема Муавра-Лапласа
- •17.Формула Пуассона
- •18.Интегральная теорема Лапласа
- •19.Наивероятнейшее число появления события
- •20.Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях
- •21.Понятие и виды случайной величины
- •23.Функция распределения вероятностей
- •25.Плотность распределения вероятностей
- •26. Числовые характеристики нсв
- •30.Биномиальное распределение
- •32.Геометрическое распределение
- •33.Гипергеометрическое распределение
- •34.Равномерное распределение
- •35. Нормальное распределение
- •36.Показательное распределение
- •45.Коэффициент корреляции
- •47.Неравенство Чебышева)
23.Функция распределения вероятностей
Т. к. способ задания случайных величин с помощью ряда распределения имеет место только для ДСВ, то естественно возникает вопрос: можно ли ввести общий способ задания для всех типов случайных величин?
Пусть
 - случайная величина, а
- некоторое действительное число.
Вероятность
- случайная величина, а
- некоторое действительное число.
Вероятность
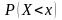 события, состоящего в том, что
примет значение, меньшее
обозначается
события, состоящего в том, что
примет значение, меньшее
обозначается
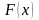 .
.
Если изменяется, то изменяется и , т.е. есть функция зависящая от .
О. 1. Функцией распределения вероятностей (интегральной функцией) называется функция , определяющая вероятность того, что случайная величина в результате испытания примет значение, меньшее , т.е.
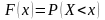 .
.
Геометрически это означает, что есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, расположенной слева от точки .
Свойства функции :
1.
Значения функции распределения
принадлежат отрезку
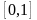 ,
т.е.
,
т.е.
 .
.
2. Функция неубывающая, т.е.
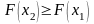 ,
если
,
если
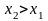 .
.
3.
Если возможные значения случайной
величины принадлежат интервалу
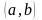 ,
то:
,
то:
1)
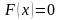 при
при
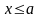 ;
;
2)
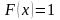 при
при
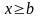 .
.
4. Вероятность того, что случайная величина примет значение, заключенное в интервале , равна приращению функции распределения на этом интервале:
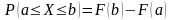 .
.
5.
Вероятность
того, что непрерывная случайная величина
примет одно определенное значение
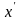 ,
равна нулю, т.е.
,
равна нулю, т.е.
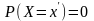 .
.
График
функции распределения вероятностей
ДСВ представляет собой ступенчатую
фигуру, а НСВ – непрерывную линию.
Причем, если речь идет о ДСВ
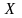 и ее возможные значения расположить в
порядке возрастания
и ее возможные значения расположить в
порядке возрастания
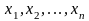 ,
то
может быть представлена в виде:
,
то
может быть представлена в виде:
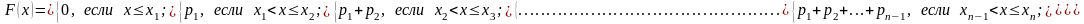
25.Плотность распределения вероятностей
О.1.
Плотностью
распределения вероятностей (дифференциальной
функцией) непрерывной случайной величины
называется функция
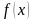 ,
равная первой производной от функции
распределения
,
т.е.
,
равная первой производной от функции
распределения
,
т.е.
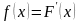 .
.
Свойства функции :
Плотность распределения неотрицательная функция, т.е.
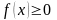 .
.Несобственный интеграл от плотности распределения на интервале
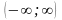 равен единице, т.е.
равен единице, т.е.
 .
.
Если все возможные значения случайной величины принадлежат интервалу , то
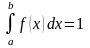 .
.
4. Вероятность попадания случайной величины в интервал может быть вычислен по формуле (Ньютона-Лейбница):
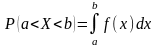 .
.
5. Если известна плотность распределения , то функция распределения может быть найдена по формуле:
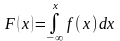
26. Числовые характеристики нсв
Пусть непрерывная случайная величина задана плотностью распределения . Тогда аналогично ДСВ для НСВ могут быть определены числовые характеристики.
О.1.
Математическим ожиданием
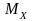 НСВ
,
возможные значения которой принадлежат
всей оси
НСВ
,
возможные значения которой принадлежат
всей оси
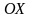 ,
называют определенный интеграл:
,
называют определенный интеграл:
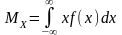 .
.
O.2.
Дисперсией
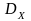 НСВ
,
возможные значения которой принадлежат
всей оси
,
называется значение интеграла
НСВ
,
возможные значения которой принадлежат
всей оси
,
называется значение интеграла
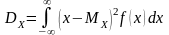 .
.
Замечание 1. Свойства математического ожидания и дисперсии ДСВ сохраняются и для НСВ.
Замечание
2. На
практике для вычисления дисперсии
удобно пользоваться формулой:
 .
.
O.3.
Средним
квадратическим отклонением
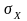 НСВ
называется корень квадратный из
дисперсии, т.е.
НСВ
называется корень квадратный из
дисперсии, т.е.
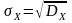 .
.
О.4.
Модой
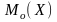 НСВ
называется такое значение этой величины,
плотность вероятности которого
максимальна.
НСВ
называется такое значение этой величины,
плотность вероятности которого
максимальна.
O.5.
Медианой
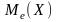 НСВ
называется такое значение этой величины,
что выполняется равенство:
НСВ
называется такое значение этой величины,
что выполняется равенство:
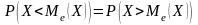 .
.
27.Математическим ожиданием НСВ , возможные значения которой принадлежат всей оси , называют определенный интеграл:
.
Модой НСВ называется такое значение этой величины, плотность вероятности которого максимальна.
O.5. Медианой НСВ называется такое значение этой величины, что выполняется равенство:
.
28. Дисперсией НСВ , возможные значения которой принадлежат всей оси , называется значение интеграла
.
Замечание 1. Свойства математического ожидания и дисперсии ДСВ сохраняются и для НСВ.
Замечание 2. На практике для вычисления дисперсии удобно пользоваться формулой: .
O.3. Средним квадратическим отклонением НСВ называется корень квадратный из дисперсии, т.е.
.
