11.Вероятность появления хотя бы одного события

В некоторых случаях вероятность события удобнее подсчитывать как вероятность противоположного другому событию.

Пусть события 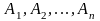попарно независимы и их вероятности известны и равны соответственно 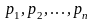, тогда вероятности противоположных им событий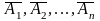 будут равны .

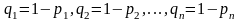Теорема 6. Вероятность появления хотя бы одного из попарно независимых событий равна разности между единицей и произведением вероятностей противоположных событий , т.е.

.

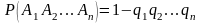12.Формула полной вероятности

Теорема. Если событие может наступить только при условии появления одного из несовместных событий 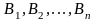, которые образуют полную группу, то вероятность события равна сумме произведений каждого из этих событий на соответствующие условные вероятности события , т. е.

.

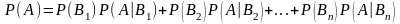Поскольку заранее не известно, какие из событий наступят, то их называют гипотезами.

13.Вероятность гипотез. Формула Байеса

Часто, приступая к анализу вероятностей, мы имеем предварительные значения вероятностей, интересующих нас событий. После проведения испытания эти вероятности могут несколько уточняться.

Пусть произведено испытание, в результате которого появилось событие . Необходимо найти вероятности гипотез , после того как испытание произведено, т. е. условные вероятности гипотез .

Найдем сначала условную вероятность .

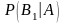По теореме умножения .

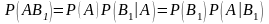Отсюда .

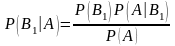Аналогично выводятся формулы остальных гипотез.

В общем случае условная вероятность любой гипотезы 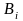, где 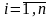, определяется как .

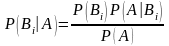Последняя формула называется формулой Байеса. Она позволяет переоценивать вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие .

14.

Пусть проводится независимых испытаний, в каждом из которых возможно только два исхода: либо событие появится, либо нет.

Условимся считать, что вероятность события в каждом испытании одна и та же и равна .

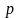Тогда вероятность ненаступления события в каждом испытании так же постоянна и равна .

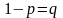15.Формула Бернулли

О. 1. Если проводится несколько испытаний, причем вероятность появления события в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события .

Теорема 1. Если вероятность наступления события в каждом из независимых испытаний постоянна, то вероятность 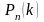того, что в независимых испытаниях событие появится ровно раз, вычисляется по формуле

.

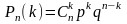16. Локальная теорема Муавра-Лапласа

При больших пользоваться формулой Бернулли становится затруднительно.

Теорема 2. Если вероятность появления события в каждом испытании постоянна и равна 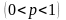, то вероятность того, что в независимых испытаниях событие появится ровно раз, приближенно вычисляется (тем точнее, чем больше ) по формуле

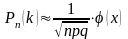, где

, .

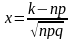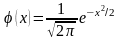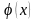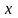Для определения значений функции существуют специальные таблицы соответствующие положительным значениям аргумента . При отрицательных значениях аргумента пользуются теми же таблицами, т. к. функция четная, т.е. .
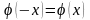