9. Теоремы умножения вероятностей

О. 1. Два события события и называются зависимыми, если вероятность появления каждого из них зависит от того, появилось ли другое событие или нет.

О. 2. Два события и называются независимыми, если вероятность появления каждого из них не зависит от того, появилось ли другое событие или нет.

О. 3. Вероятности независимых событий называются безусловными.

Пусть и зависимые события.

О. 4. Условной вероятностью события называется вероятность этого события, вычисленная в предположении, что событие уже произошло.

Обозначается или .

Условная вероятность события определяется аналогично.

Теорема 1. Если и независимые события, то их условные вероятности совпадают с обычными вероятностями, т. е.

,

.

Пусть даны два события и и требуется найти вероятность их совместного появления.

Теорема 2. Если и зависимые события, то вероятность их совместного появления (произведения) равна произведению вероятности одного из этих событий на условную вероятность другого, вычисленную при условии, что первое событие произошло, т. е.

,

.

Следствие: Вероятность совместного появления (произведения) нескольких зависимых событий равна произведению вероятности одного из этих событий на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие уже произошли, т. е.

.

Пусть даны два события и и требуется найти вероятность их совместного появления.

Теорема 2. Если и зависимые события, то вероятность их совместного появления (произведения) равна произведению вероятности одного из этих событий на условную вероятность другого, вычисленную при условии, что первое событие произошло, т. е.

,

.

Следствие: Вероятность совместного появления (произведения) нескольких зависимых событий равна произведению вероятности одного из этих событий на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие уже произошли, т. е.

.

Теорема 3. Если события и независимые, то вероятность их совместного появления (произведения) равна произведению их вероятностей, т. е.

.

Следствие: Вероятность совместного появления (произведения) нескольких независимых событий равна произведению вероятностей данных событий, т. е.

10.Теоремы сложения вероятностей

Пусть даны два события и требуется определить вероятность появления хотя бы одного из этих событий.

Теорема 4. Если события и несовместные, то вероятность появления одного из этих событий (сумма) равна сумме вероятностей данных событий, т.е.

.

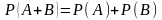Следствия:

Вероятность суммы нескольких несовместных событий равна сумме вероятностей этих событий, т. е.

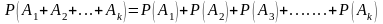
Если события образуют полную группу событий, то сумма их вероятностей равна единице.

Сумма вероятностей двух противоположных событий равна единице.

Теорема 5. Если события и совместные, то вероятность появления хотя бы одного из этих событий (сумма) равна сумме вероятностей этих событий без вероятности их совместного появления, т. е.

.
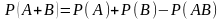