1. Элементы комбинаторики.
Правило суммы. Если элемент A1 можно выбрать n1 способами, A2 можно выбрать n2 способами, ...., Ak можно выбрать nK
Способами отличными от всех предыдущих то выбор 1 – ого из элементов A1, A2 ……..Ak элементов моет быть осуществлен n1+n2+…..nk способами.
Правило произведения. Пусть элемент A1 можно выбрать n1 способами, после каждого такого выбора A2 можно выбрать n2 способами, после (k-1) – го выбора элемент Ak можно выбрать nK способами, тогда выбор всех элементов A1,A2….Ak в указанном порядке может быть осуществлен n1 * n2*……*nk
2.Основные комбинаторные соединения
Пусть дано множество из n элементов. Из этого множества могут быть составлены подмножества(комбинации) по m элемент ()<m<n трех видов: перестановки, размещения и сочетания.
Перестановки(m=n)
Определение. Перестановками без повторений называют комбнации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их следования. Число всевозможных перестановок без повторений Pn=n!(факториал)
Размещение и сочетание(m<n)
Опр. Размещениями без повторений называют комбинации, составленные из n различных элементов по m элементов, которые отличатся либо составом элемента либо порядком следования. Число всевозможных размещений без повторений
A(по m из n) = n!/(n-m)! = n(n-1)(n-2)…….(n-m+1)
Опр. Сочетаниями без повторений называются комбинации, составленные из n различных элементов по m элементов, которые отличаются только составом.
Число сочетаний без повторений C по m из n = n!/m!(n-m)!
Свойства сочетаний:
С по 0 из n = 1
С по 1 из n = n
C по n из n = 1
3. Испытание. Событие. Классификация событий
О. 1: Испытание – это многократное воспроизведение одного и того же комплекса условий, при котором производится наблюдение.
Качественный результат испытания – событие.
О. 2: Множество взаимоисключающих исходов одного испытания называется множеством элементарных событий или элементарных исходов.
События
обозначаются заглавными буквами
латинского алфавита:
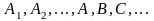
Наблюдаемые события (явления) можно подразделить на следующие три вида: достоверные, невозможные, случайные.
О. 3: Событие называется достоверным, если в результате испытания оно обязательно произойдет.
О. 4: Событие называется невозможным, если в результате испытания оно никогда не произойдет.
О. 5: Событие называется случайным, если в результате испытания оно может либо произойти, либо не произойти.
Случайные события (явления) можно подразделить на следующие виды: совместные, несовместные, противоположные, равновозможные.
О. 6: Два события называются совместными, если при одном испытании, появление одного из них не исключает появление другого.
О. 7: Два события называются несовместными, если при одном испытании, появление одного из них исключает появление другого.
О. 8: Несколько событий образуют полную группу в данном испытании, если они попарно несовместны и в результате испытания одно из этих событий обязательно появится.
О. 9: Два несовместных события, образующих полную группу называются противоположными.
Событие
противоположное событию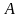
обозначается
.
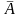О. 10: События называются равновозможными, если есть основания считать, что одно из них не является более возможным, чем другое.
4.Понятие вероятности события
О. 1. Вероятностью события называется численная мера степени объективной возможности наступления события в данном испытании.
Выбор числового значения вероятности в конкретной задаче осуществляется либо при обработке результатов большого количества испытаний, либо предполагается теоретически ( например по свойству симметрии).
Классическое определение вероятности и его свойства
Пусть
в результате испытания может наступить
конечное число
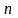равновозможных элементарных событий
(исходов), причем среди них имеются
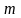таких исходов, которые ведут к появлению
события
.
Эти
событий называются благоприятствующими
событию
.
О.
2.
(классическое
определение)
Вероятностью
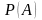события
называется отношение числа элементарных
событий благоприятствующих событию
к числу всех элементарных событий:
,
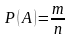где - общее число элементарных событий,
- число элементарных событий благоприятствующих событию .
Свойства вероятности
Вероятность
достоверного события
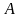равна единице, т. к.
;
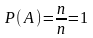Вероятность невозможного события равна нулю, т. к.
;
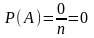Вероятность случайного события есть положительное число, заключенное между нулем и единицей, т. к.
,
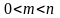то
.
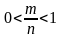Недостатки классического определения.
1. Определение не применимо, если число элементарных исходов испытания бесконечно.
2. Часто не возможно представить результат испытания в виде совокупности элементарных событий.
3. Трудно указать основания, позволяющие считать события равновозможными. О равновозможности исходов опыта заключают из соображений симметрии.
Для преодоления 3 недостатка вводятся статистические вероятности, а для преодоления 1 недостатка – геометрические (вероятности попадания точки в область). Рассмотрим более подробно понятие статистической вероятности.