Ответы к экзамену по информатике

1. Предмет информатики. Понятие информации. Понятие количества информации. Единицы измерения информации.

Информатика – фундаментальная естественная наука, изучающая процессы, передачи, обработки информации.

2. Сообщение, сигнал, носители информации. Преобразование информации в системах передачи информации.

3. Понятие спектра сигнала на примерах гармоники, модулированной по амплитуде.

4. Способы цифрового кодирования.

Потенциальный код без возвращения к нулю (Non return to Zero, NRZ) При передаче последовательности единиц сигнал не возвращается к нулю в течении такта. Метод NRZ прост в реализации, обладает хорошей распознаваемостью ошибок, но обладает свойством синхронизации. Поэтому при высоких скоростях обмена данными и длинных последовательностей единиц или нулей небольшое рассогласование тактовых частот может привести к ошибке в целый такт и, соответственно, считыванию некорректного значения бита. В чистом виде код NRZ в сетях не используется.

Биполярный код с альтернативной инверсией (Bipolar Alternate Mark Inversion, AMI) В этом методе используются три уровня потенциала - отрицательный, нулевой и положительный. Для кодирования логического нуля используется нулевой потенциал, а логическая единица кодируется либо положительным потенциалом, либо отрицательным, при этом потенциал каждой новой единицы противоположен потенциалу предыдущей. В целом, для различных комбинаций битов на линии использование кода AMI приводит к более узкому спектру сигнала, чем для кода NRZ, а значит, и к более высокой пропускной способности линии.

Потенциальный код с инверсией при единице (Non return to Zero with ones Inverted, NRZI) Существует код, похожий на AMI, но только с двумя уровнями сигнала. При передаче нуля он передает потенциал, который был установлен в предыдущем такте (то есть не меняет его), а при передаче единицы потенциал инвертируется на противоположный. Он удобен в тех случаях, когда наличие третьего уровня сигнала весьма нежелательно, например в оптических кабелях, где устойчиво распознаются два состояния сигнала - свет и темнота.

Биполярный импульсный код Кроме потенциальных кодов в сетях используются и импульсные коды, в которых данные представлены полным импульсом или же его частью - фронтом. Наиболее простым случаем такого подхода является биполярный импульсный код, в котором единица представлена импульсом одной полярности, а нуль - другой. Каждый импульс длится половину такта. Такой код обладает отличными самосинхронизирующими свойствами, но постоянная составляющая может присутствовать, например, при передаче длинной последовательности единиц или нулей. Кроме того, спектр у него шире, чем к потенциальных кодов, из-за этого он используется редко.

Манчестерский код В манчестерском коде для кодирования нулей и единиц используется перепад потенциала, то есть фронт импульса. Единица кодируется перепадом от низкого уровня сигнала к высокому, а ноль - обратным перепадом. В начале каждого такта может происходить служебный перепад сигнала, если нужно представить несколько единиц или нулей подряд. В среднем ширина полосы манчестерского кода в полтора раза уже, чем у биполярного импульсного кода. Манчестерский код имеет еще одно преимущество перед биполярным импульсным кодом. В последнем для передачи данных используется три уровня сигнала, а в манчестерском - два.

Потенциальный код 2B1Q Потенциальный код с четырьмя уровнями сигнала для кодирования данных. Этот код 2B1Q название которого отражает его суть - каждые два бита (2B) передаются за один такт сигналом, имеющем четыре состояния (1Q). Паре бит 00 соответствует потенциал -2,5 В; паре бит 01 - потенциал -0,833 В; паре 11 - потенциал +0,833; паре 10 - потенциал +2,5 В. При этом способе кодирования требуются дополнительные меры по борьбе с длинными последовательностями одинаковых пар битов, так как при этом сигнал превращается в постоянную составляющую. При случайном чередовании битов спектр сигналов в два раза уже, чем у кода NRZ, так как при той же битовой скорости, длительность такта увеличивается в два раза. Таким образом, с помощью кода 2B1Q можно по одной и той же линии передавать данные в два раза быстрее, чем с помощью кода AMI или NRZI. Однако для его реализации мощность передатчика должно быть выше, чтобы четыре уровня четко различались приемником на фоне помех.

5. Основные параметры линии связи.

Характеристики линий связи можно разделить на две группы:

• параметры распространения характеризуют процесс распространения полезного сигнала в зависимости от собственных параметров линии, например погонной индуктивности медного кабеля;

• параметры влияния описывают степень влияния на полезный сигнал других сигналов - внешних помех, наводок от других пар проводников в медном кабеле.

6. Представление информации в ЭВМ. Кодирование чисел. Целое со знаком. Представление целого числа в дополнительном коде. Обратный код.

В ЭВМ применяется двоичная система счисления, т.е. все числа в компьютере представляются с помощью нулей и единиц, поэтому компьютер может обрабатывать только информацию, представленную в цифровой форме.

Для преобразования числовой, текстовой, графической, звуковой информации в цифровую необходимо применить кодирование. Кодирование – это преобразование данных одного типа через данные другого типа. В ЭВМ применяется система двоичного кодирования, основанная на представлении данных последовательностью двух знаков: 1 и 0, которые называются двоичными цифрами (binary digit – сокращенно bit).

Таким образом, единицей информации в компьютере является один бит, т.е. двоичный разряд, который может принимать значение 0 или 1. Восемь последовательных бит составляют байт. В одном байте можно закодировать значение одного символа из 256 возможных (256 = 2 в степени 8). Более крупной единицей информации является килобайт (Кбайт), равный 1024 байтам (1024 = 2 в степени 10). Еще более крупные единицы измерения данных: мегабайт, гигабайт, терабайт (1 Мбайт = 1024 Кбайт; 1 Гбайт = 1024 Мбайт; 1 Тбайт = 1024 Гбайт).

Целые числа кодируются двоичным кодом довольно просто (путем деления числа на два).

Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1. Далее пример с числом 26 и -26 соответственно.

0 00011010 – положительное число 1 00011010 – отрицательное число

Обратный код – это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.

Дополнительный код – это обратный код, к младшему значащему разряду которого прибавлена единица.

Для положительных чисел прямой, дополнительный и обратный коды одинаковые. Для отрицательных чисел они разные. Чтобы получить дополнительный код отрицательного числа, необходимо перевести прямой код в обратный, инвертировав все разряды, т.е. поменяв все 1 на 0, а 0 на 1 (знаковый разряд не трогают). После чего добавить к получившемуся коду 1.

Пример на числе -98: 1100010 (2СС) > 1 1100010 (прямой код) > 1 0011101 (обратный код) > 1 0011110 (дополнительный код)

Пример на числе 98: 1100010 (2СС) > 0 1100010 (прямой код) > 1 1100010 (обратный код) > 1 1100010 (дополнительный код)

7. Числа в форме с плавающей точкой.

Чтобы представить число с плавающей точкой в двоичном коде, необходимо сначала перевести целое десятичное число в двоичную систему счисления, затем отдельно дробную часть последовательно умножать на 2. В результате каждый раз записываем целую часть произведения. Затем соединяем обе части и получаем число с плавающей точкой в двоичной системе счисления.

8. Понятие файла. Исполняемые файлы. Кодирование символьной информации, кодирование команд.

Понятие файла Файл — это поименованная область на диске или другом носителе информации. В файлах могут храниться тексты программ, документы, готовые к выполнению программы и любые другие данные. Текстовые и двоичные файлы. Часто файлы разделяют на две категории — текстовые и двоичные. Текстовые файлы предназначены для чтения человеком. Они состоят из строк символов, причем каждая строка оканчивается двумя специальными символами «возврат каретки» (СR) и «новая строка» (LF). При редактировании и просмотре текстовых файлов эти специальные символы, как правило, не видны, В текстовых файлах хранятся тексты программ, командных файлов и т.д. Файлы, не являющиеся текстовыми, по традиции называются двоичными.

Исполнимые файлы Каждая программа (кроме операционной системы, которая запускается при включении компьютера) содержит в своем составе файл, который запускает эту программу. Такой файл называется исполнимым файлом. Иначе говоря, исполнимый файл —это головной файл программы, запускающий ее на выполнение. Если программа состоит из одного файла, то этот файл и является исполнимым файлом. По традиции исполнимые файлы обычно имеют расширение имени .СОМ или .ЕХЕ.

Файлы документов Кроме файлов программ, на Ваших дисках всегда будут файлы, содержащие данные, с которыми Вы работаете. Чаще всего данные, соответствующие одному документу, с которым Вы работаете, содержатся в одном файле. Такие файлы обычно называют файлами документов. Например, большинство редакторов текстов, электронных таблиц, сохраняют любой обрабатываемый документ (таблиц; рисунок и т.д.) в одном файле. Для работы с такими документами надо запустить соответствующую программу и считать (часто говорят — открыть) документа в этой программе.

Имена файлов Чтобы операционная система и другие программы могли обращаться к файлам, файлы должны иметь обозначения. Это обозначения обычно называют именем файла. В операционной системе DOS, обозначения файлов состоят из двух частей: имени и расширения. Часто имя и расширение вместе также называются именем, как правило, это не приводит к путанице. Расширение начинается с точки, за которой следуют от 1 до 3 символов. Например, Command.exe, имя.расширение/формат

Допустимые символы Имя и расширение могут состоять из прописных и строчных латинских букв, цифр и символов.

Прописные и строчные буквы В имени и расширении имени файла прописные и строчные латинские буквы являются эквивалентными, так как DOS переводит все строчные буквы в соответствующие прописные буквы. На диске имя файла хранится в версии, записанной прописными (то есть большими) буквами.

Русские буквы Некоторые «русифицированные» версии DOS позволяют употреблять в именах файлов русские буквы. Однако эту возможность следует использовать с осторожностью: многие программы не «понимают» имен с русскими буквами.

Расширение имени Расширение имени файла является необязательным. Оно, как правило, описывает содержание файла, поэтому использование расширения весьма удобно. Многие программы устанавливают расширение имени файла, и по нему Вы можете узнать, какая программа создала файл. Кроме того, многие программы (Norton commander, Диспетчер Файлов Windows и т.д.) позволяют по расширению имени файла вызвать соответствующую программу и сразу загрузить в нее данный файл — это весьма полезно, так как экономит время.

Примеры: .com,.exe-исполнимые файлы (готовые к выполнению программы); .bat-командные файлы; .pas-программы на Паскале; .bak- копия файла, создаваемая перед его изменением; .sys-системный или драйверный файл; .txt –текстовый файл; .tmp-рабочий временный файл; .rar, .arj, .zip-архивные.

Кодирование символьной информации Для кодирования символьной информации в компьютере используется кодовая таблица ASCII (American Standart Code for Information Interchange) - стандартный американский код для обмена информацией. Эта таблица условно делится на две части. Первая часть кодов от 0 до 127 отведена для английских букв, цифр, различных символов, математических операций. Вторая часть является расширением основной таблицы кодов. Она используется для кодировки знаков различных национальных алфавитов.

Таблица кодов выглядит следующим образом:

При использовании данной таблицы можно закодировать 256 разных символов. Хотя в настоящее время все более популярным становится другой стандарт кодирования - Unicode. В этой системе вместо 8-битного кодирования используется 16-битное кодирование. Длина кодового слова равна 2 байтам. При этом можно закодировать целых 65536 символов. С помощью Unicode можно закодировать все национальные алфавиты одновременно.

Теперь рассмотрим принцип кодирования ASCII на конкретном примере. Необходимо закодировать слово КОМПЬЮТЕР с помощью таблицы ASCII-кодов. Необходимо действовать следующим образом. Из таблицы мы видим, что каждая буква русского алфавита (или латинского) стоит на пересечении двух чисел шестнадцатеричной системы счисления (подобно таблице Пифагора). Для кодирования одного символа надо взять соответствующее число сначала по горизонтали, потом по вертикали. В результате мы получим следующий код: 8A 8E 8C 8F 9C 9E 92 90. Декодирование происходит аналогично. Далее компьютер переводит полученный код в двоичную форму и размещает в своей памяти.

Кодирование команд Кодировать команды процессора можно различными способами, в зависимости от разрядности процессора, а также от наличия и свойств некоторых внутренних объектов процессора. Формат команды обычно соответствует разрядности процессора – если процессор, к примеру, 8-разрядный, то и основные команды тоже должны быть восьмиразрядными. Если процессор 32-разрядный, то и команда должна быть 32-разрядной. Чтобы сформулировать некоторые команды, разрядности процессора может не хватить, и тогда команда может состоять из двух слов. Для 8-разрядных процессоров эта ситуация типична, в 32-разрядных – встречается реже.

Трехадресные команды Если необходимо вычислить, к примеру, сумму двух регистров, то можно сформулировать команду в виде 32 разрядного слова, разбитого на 4 группы разрядов:

Код команды сложения

Адрес регистра, содержащего первое слагаемое

Адрес регистра, содержащего второе слагаемое

Адрес регистра для размещения результат

Это означает, что процессор должен выбрать из регистрового файла первое слагаемое и записать его в один из входных регистров АЛУ. Затем выбрать из регистрового файла второе слагаемое, и поместить его в другой входной регистр. Затем нужно данные с выхода АЛУ записать в регистровый файл. Все три адреса, необходимых для обращения к регистровому файлу, будут содержаться в самой команде. Такой формат команды называется трехадресным, и наиболее удобен для понимания. 32-разрядного слова вполне достаточно, для этого формата. Если разбить 32 разряда на 4 равные группы, в каждой группе будет по 8 разрядов. При помощи 8 разрядов можно закодировать 256 различных значений, значит, регистров у такого процессора может быть 256, и самих команд тоже может быть 256. Однако если попробовать 8-разрядную команду сделать трехадресной, получится плохо – в группе будет по 2 разряда, значит регистров может быть 4, и команд тоже может быть только четыре. Или, если сделать группы неодинаковыми, то можно закодировать 16 команд, но регистров тогда можно будет указывать только два. Поэтому такой формат предпочтительнее для процессоров с разрядностью 32 и более.

Двухадресные команды Если нужно уложиться в более короткое слово, например 16 разрядов, можно договориться, что результат операции будет записан по адресу, содержащему второе слагаемое. Тогда команда будет выглядеть так:

Код команды сложения

Адрес регистра, содержащего первое слагаемое

Адрес регистра, содержащего второе слагаемое и результат

В этом случае, процессор должен также последовательно выбрать оба аргумента из регистрового файла, а результат поместить по тому же адресу, где находилось второе слагаемое. Такой формат тоже достаточно удобен, но имеет тот недостаток, что после выполнения операции один из аргументов будет потерян. Хотя во многих случаях это не очень важно. Такой формат команды называется двухадресным. При двухадресном формате команды и разрядности 16 можно закодировать 64 команды (код операции длинной 6 разрядов), которые можно выполнять над 32 регистрами (2 поля по 5 разрядов).

Одноадресные команды В случае, когда с разрядностью совсем плохо, полезно иметь в процессоре регистр со специальными свойствами – аккумулятор. По конструкции, аккумулятор представляет собой самый обычный регистр. От других регистров он отличается не конструкцией, а своим особым предназначением. Особое предназначение аккумулятора определяется соглашением, согласно которому в качестве одного из аргументов команды всегда используется аккумулятор, и в нем же всегда сохраняется результат выполнения команды. Тогда в самой команде нам потребуется указать только один адрес:

Код команды сложения

Адрес регистра

Правда, в этом случае могут понадобиться дополнительные команды для помещения другого аргумента в аккумулятор, и для сохранения результата из аккумулятора в каком-либо из регистров. Такой формат команды наименее удобен для восприятия и программирования, но зато позволяет при небольшом объеме регистрового файла уместить многие команды в короткое слово из восьми разрядов и больше всего подходит для восьмиразрядных процессоров. При разрядности 8, такой формат позволяет указывать 16 регистров (4 разряда на адрес регистра) и кодировать 16 различных команд (4 разряда на код операции).

9. Преобразование сигнала из аналогового формы в дискретную. Кодирование. Параметры кода. Двоичные коды: двоичный, двоично-десятичный.

По видам (типам) сигналов выделяются следующие:

• Аналоговый

• Цифровой

• Дискретный

Аналоговый сигнал является естественным. Его можно зафиксировать с помощью различных видов датчиков. Например, датчиками среды (давление, влажность) или механическими датчиками (ускорение, скорость). Аналоговые сигналы в математике описываются непрерывными функциями. Электрическое напряжение описывается с помощью прямой, т.е. является аналоговым.

Цифровые сигналы являются искусственными, т.е. их можно получить только путем преобразования аналогового электрического сигнала.

Процесс последовательного преобразования непрерывного аналогового сигнала называется дискретизацией. Дискретизация бывает двух видов:

• по времени

• по амплитуде

Дискретизация по времени обычно называется операцией выборки. А дискретизация по амплитуде сигнала - квантованием по уровню.

В основном цифровые сигналы являются световыми или электрическими импульсами. Цифровой сигнал используют всю данную частоту (полосу пропускания). Этот сигнал все равно остается аналоговым, только после преобразования наделяется численными свойствами. И к нему можно применять численные методы и свойства.

Дискретный сигнал – это все тот же преобразованный аналоговый сигнал, только он необязательно квантован по уровню.

Кодирование информации — процесс преобразования сигнала из формы, удобной для непосредственного использования информации, в форму, удобную для передачи, хранения или автоматической переработки.

Преобразование сигнала из аналоговой формы в дискретную А как же все-таки получить из аналогового цифровой сигнал? Ответом является данная тема - аналого-цифровой преобразователь (АЦП).

Происходит следующее. Аналоговый сигнал посредством аналого-цифрового преобразователя (АЦП) трансформируется в значение в двоичной системе счисления. Но, естественно, что существует погрешность данного преобразования. Она называется - погрешность оцифровки и зависит от разрядности аналого-цифрового преобразователя (АЦП) и от частоты выборки значений преобразуемого аналогового сигнала.

Схема АЦП

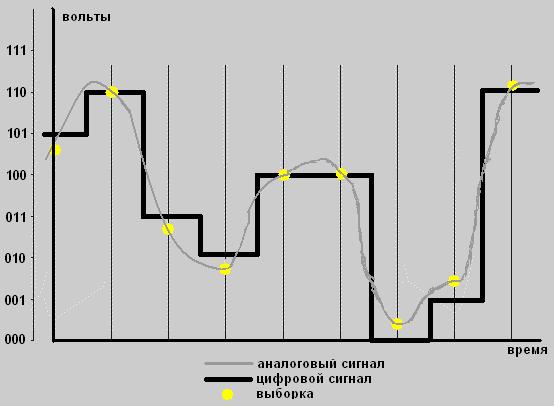
На схеме АЦП Амплитуда (вертикальная линия) разбита на 8 отрезков. Так как в двоичной системе мы целиком можем закодировать эти 8 значений тремя разрядами. А выборка происходит через равный интервал времени. На выходе мы получаем бинарный (двоичный) код:

(101)(110)(011)(010)(100)(100)(000)(001)(110)

Т.е. данный двоичный код и есть наш электрический сигнал последовательности ударов (импульсов), который вытекает из схемы АЦП.

В аналого-цифровом преобразователе большую роль играет первоначальное техническое оснащение системы (куда в частности будет поступать аналоговый сигнал). К примеру сказать, при записи речи первичным является микрофон. Т.е. и многое будет зависеть от его критериев качества:

• точность представления физической величины

• диапазон выходного сигнала

• уровень погашения помех (шумов)

Параметры кодов

Двоичный код В цифровой технике способ представления данных (чисел, слов и других) в виде комбинации двух знаков, которые можно обозначить как 0 и 1. Знаки или единицы ДК называют битами.

Одним из обоснований применения ДК является простота и надежность накопления информации в каком-либо носителе в виде комбинации всего двух его физических состояний, например в виде изменения или постоянства магнитного потока в данной ячейке носителя магнитной записи.

Наибольшее число, которое может быть выражено двоичным кодом, зависит от количества используемых разрядов, т.е. от количества битов в комбинации, выражающей число. Например, для выражения числовых значений от 0 до 7 достаточно иметь 3-разрядный или 3-битовый код:

Числовое значение	Двоичный код
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Отсюда видно, что для числа больше 7 при 3-разрядном коде уже нет кодовых комбинаций из 0 и 1.

Переходя от чисел к физическим величинам, сформулируем вышеприведенное утверждение в более общем виде: наибольшее количество значений m какой-либо величины (температуры, напряжения, тока и др.), которое может быть выражено двоичным кодом, зависит от числа используемых разрядов n как m=2n. Если n=3, как в рассмотренном примере, то получим 8 значений, включая ведущий 0.

Двоично-десятичный код Иногда бывает удобно хранить числа в памяти процессора в десятичном виде (Например, для вывода на экран дисплея). Для записи таких чисел используются двоично-десятичные коды. Для записи одного десятичного разряда используется четыре двоичных бита. Эти четыре бита называются тетрадой. Иногда встречается название, пришедшее из англоязычной литературы: нибл. При помощи четырех бит можно закодировать шестнадцать цифр. Лишние комбинации в двоично-десятичном коде являются запрещенными. Таблица соответствия двоично-десятичного кода и десятичных цифр приведена ниже:

Двоично-десятичный код				Десятичный код
0	0	0	0		0
0	0	0	1		1
0	0	1	0		2
0	0	1	1		3
0	1	0	0		4
0	1	0	1		5
0	1	1	0		6
0	1	1	1		7
1	0	0	0		8
1	0	0	1		9

Остальные комбинации двоичного кода в тетраде являются запрещенными. Запишем пример двоично-де

1258 = 0001 0010 0101 1000

В первой тетраде записана цифра 1, во второй — 2, в третьей — 5, а в последней тетраде записана цифра 8. В данном примере для записи числа 1258 потребовалось четыре тетрады. Количество ячеек памяти микропроцессора зависит от его разрядности. При 16-разрядном процессоре все число уместится в одну ячейку памяти.

589 = 0000 0101 1000 1001

В данном примере для записи числа достаточно трех тетрад, но ячейка памяти 16-разрядная. Поэтому старшая тетрада заполняется нулями. Они не изменяют значение цифры. Если бы мы заполнили нулями младшую тетраду, то число увеличилось бы в десять раз!

При записи десятичных чисел часто требуется записывать знак числа и десятичную запятую (в англоязычных странах точку). Двоично-десятичный код часто применяется для набора телефонного номера или набора кодов телефонных служб. В этом случае кроме десятичных цифр часто применяются символы '*' или '#'. Для записи этих символов в двоично-десятичном коде применяются запрещенные комбинации.

Двоично-десятичный код				Дополнительный символ
1	0	1	0		* (звёздочка)
1	0	1	1		# (решётка)
1	1	0	0		+ (плюс)
1	1	0	1		– (минус)
1	1	1	0		, (десятичная запятая)
1	1	1	1		Символ гашения

Достаточно часто в памяти процессора для хранения одной десятичной цифры выделяется одна ячейка памяти (восьми, шестнадцати или тридцатидвухразрядная). Это делается для повышения скорости работы программы. Для того, чтобы отличить такой способ записи двоично-десятичного числа от стандартного, способ записи десятичного числа, как это показано в примере, называется упакованной формой двоично-десятичного числа. Запишем те же числа, что и в предыдущем примере в неупакованном двоично-десятичном коде для восьмиразрядного процессора:

1258 = 00000001 00000010 00000101 00001000

В первой строке записана цифра 1, во второй - 2, в третьей - 5, а в последней строке записана цифра 8. В данном примере для записи числа 1258 потребовалось четыре строки (ячейки памяти)

589 = 00000000 00000101 00001000 00001001

Суммирование двоично-десятичных чисел Суммирование двоично-десяичных чисел можно производить по правилам обычной двоичной арифметики, а затем производить двоично-десятичную коррекцию. Двоично-десятичная коррекция заключается в проверке каждой тетрады на допустимые коды. Если в какой либо тетраде обнаруживается запрещенная комбинация , то это говорит о переполнении. В этом случае необходимо произвести двоично-десятичную коррекцию. Двоично-десятичная коррекция заключается в дополнительном суммировании числа шесть (число запрещенных комбинаций) с тетрадой, в которой произошло переполнение или произошёл перенос в старшую тетраду. Приведём два примера:

10. Понятие о помехоустойчивых кодах. Простейшие коды, обнаруживающие и исправляющие ошибки (с проверкой на четность, с повторением)

Помехоустойчивым (корректирующим) кодированием называется кодирование при котором осуществляется обнаружение либо обнаружение и исправление ошибок в принятых кодовых комбинациях.

Возможность помехоустойчивого кодирования осуществляется на основании теоремы, сформулированной Шенноном, согласно ей:

если производительность источника (Hи’(A)) меньше пропускной способности канала связи (Ск), то существует по крайней мере одна процедура кодирования и декодирования при которой вероятность ошибочного декодирования сколь угодно мала, если же производительность источника больше пропускной способности канала, то такой процедуры не существует.

Основным принципом помехоустойчивого кодирования является использование избыточных кодов, причем если для кодирования сообщения используется простой код, то в него специально вводят избыточность. Необходимость избыточности объясняется тем, что в простых кодах все кодовые комбинации являются разрешенными, поэтому при ошибке в любом из разрядов приведет к появлению другой разрешенной комбинации, и обнаружить ошибку будет не возможно. В избыточных кодах для передачи сообщений используется лишь часть кодовых комбинаций (разрешенные комбинации). Прием запрещенной кодовой комбинации означает ошибку. Причем, в процессе приема закодированного сообщения возможны три случая.

Прием сообщения без ошибок является оптимальным, но возможен только если канал связи идеальный. В этом случае помехоустойчивое декодирование не нужно.

В реальном канале из-за воздействия помех происходят ошибки в принимаемых кодовых комбинациях. Если принимаемая кодовая комбинация в результате воздействия помех перешла (трансформировалась) из одной разрешенной комбинации в другую, то определить ошибку не возможно, даже при использовании помехоустойчивого кодирования.

Если же передаваемая разрешенная кодовая комбинация, в результате воздействия помех, трансформируется в запрещенную комбинация, то в этом случае существует возможность обнаружить ошибку и исправить ее.

Помехоустойчивое кодирование может осуществляться двумя способами: с обнаружением ошибок либо с исправлением ошибок. Возможность кода обнаруживать или исправлять ошибки определяется кодовым расстоянием.

Если осуществляется кодирование с обнаружением ошибок, то кодовое расстояние должно быть хотя бы на единицу больше чем кратность обнаруживаемых ошибок, т. е.

d₀? q_{о ош} + 1

Если данное условие не выполняется, то одни из ошибок обнаруживаются, а другие нет.

Если осуществляется кодирование с исправлением ошибок, то кодовое расстояние должно быть хотя бы на единицу больше удвоенного значения кратности исправляемых ошибок, т. е.

d₀? 2q_{и ош} + 1

Если данное условие не выполняется, то одни из ошибок исправляются, а другие нет.

Следует отметить, что если код способен исправить одну ошибку (q_{и ош} = 1), что соответствует кодовому расстоянию 3 (d0 = 1?2+1 = 3), то обнаружить он может две ошибки, т. к.

q_{о ош} = d₀ – 1 = 2

Код с проверкой на четность Независимо от длины кодовой комбинации этот код имеет один проверочный элемент и обозначается как (n,n-1) - код. Значение проверочного элемента выбирается из условия получения четного числа единиц, т.е. общее число единиц в любом разрешенном кодовом слове четное. Этот код имеет dмин=2 и обнаруживает все ошибки нечетной кратности. Если в качестве первичного используется код МТК-2 (n=5), то n=6, r=1. Коэффициент избыточности Ки=0,17, что частично объясняет низкую эффективность кода.

Существует также код с двумя проверками на четность. Независимо от длины кодовой комбинации этот код имеет два проверочных элемента, один из которых выбирается из условия четности всех информационных разрядов, а второй - из условия четности всех нечетных (или четных) по номеру информационных разрядов. Этот код обнаруживает часть ошибок четной кратности - все смежные, рядом расположенные ошибки.

Код с повторением коды, в которых один заданный информационный символ повторяется n раз (обычно n нечетно) и поэтому считается низкоскоростным. Код с повторением имеет длину n=nk, минимальное кодовое расстояние dмин=n. Избыточность кода равна (n-1)/n.

Код с повторением характеризуется довольно высокими исправляющими свойствами при действии пакетов ошибок. Так при n=2 всегда исправляются пакеты ошибок до n/2. Недостатком кодов с повторением является весьма высокая избыточность. Даже при двукратном повторении коэффициент избыточности равен 0,5.

11. Групповые линейные коды. Код Хэмминга, циклические коды. Способы задания кодов. Порождающая и проверочная матрицы.

Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.

Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение.

Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.

Циклические коды Линейный код называют циклическим, если для любого кодового слова [x_nx₀x₁...x_n-1] циклическая перестановка символов [x₀x₁...x_n-1x_n] также дает кодовое слово.

Вторым свойством всех разрешенных комбинаций циклических кодов является их делимость без остатка на некоторый выбранный полином, называемый производящим.

Эти свойства используются при построении кодов, кодирующих и декодирующих устройств, а также при обнаружении и исправлении ошибок.

Циклические коды — это целое семейство помехоустойчивых кодов, включающее в себя в качестве одной из разновидностей коды Хэмминга, но в целом обеспечивающее большую гибкость с точки зрения возможности реализации кодов с необходимой способностью обнаружения и исправления ошибок, возникающих при передаче кодовых комбинаций по каналу связи. Циклический код относится к систематическим блочным (n, k)-кодам, в которых k первых разрядов представляют собой комбинацию первичного кода, а последующие (n − k) разрядов являются проверочными.

В основе построения циклических кодов лежит операция деления передаваемой кодовой комбинации на порождающий неприводимый полином степени r. Остаток от деления используется при формировании проверочных разрядов. При этом операции деления предшествует операция умножения, осуществляющая сдвиг влево k-разрядной информационной кодовой комбинации на r разрядов.

При декодировании принятой n-разрядной кодовой комбинации опять производится деление на порождающий полином.

Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на производящий полином. Если синдром равен нулю, то считается, что ошибок нет. В противном случае, с помощью полученного синдрома можно определить номер разряда принятой кодовой комбинации, в котором произошла ошибка, и исправить ее.

Однако не исключается возможность возникновения в кодовых комбинациях многократных ошибок, что может привести к ложным исправлениям и/или не обнаружению ошибок при трансформации одной разрешенной комбинации в другую.

12. Позиционные системы исчисления: десятичная, шестнадцатеричная, восьмеричная, двоичная. Перевод представления числа из одной системы исчисления в другую.

Позиционная система счисления (позиционная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).

Десятичная система счисления Основание этой системы счисления p равно десяти. В этой системе счисления используется десять цифр. В настоящее время для обозначения этих цифр используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число в десятичной системе счисления записывается как сумма единиц, десятков, сотен, тысяч и так далее. То есть веса соседних разрядов различаются в десять раз. Точно также записываются и числа, меньшие единицы. В этом случае разряды числа будут называться как десятые, сотые или тысячные доли единицы.

Рассмотрим пример записи десятичного числа. Для того чтобы показать, что в примере используется именно десятичная система счисления, используем индекс 10. Если же кроме десятичной формы записи чисел не предполагается использования никакой другой, то индекс обычно не используется:

A₁₀=247,56₁₀=2*10²+4*10¹+7*10⁰+5*10^-1 +6*10^-2=200₁₀+40₁₀+7₁₀+0,5₁₀+0,06₁₀

Здесь самый старший разряд числа будет называться сотнями. В приведённом примере сотням соответствует цифра 2. Следующий разряд будет называться десятками. В приведённом примере десяткам соответствует цифра 4. Следующий разряд будет называться единицами. В приведённом примере единицам соответствует цифра 7. Десятым долям соответствует цифра 5, а сотым – 6.

Двоичная система счисления Основание этой системы счисления p равно двум. В этой системе счисления используется две цифры. Чтобы не выдумывать новых символов для обозначения цифр, в двоичной системе счисления были использованы символы десятичных цифр 0 и 1. Для того чтобы не спутать систему счисления в записи числа используется индекс 2. Если же кроме двоичной формы записи чисел не предполагается использования никакой другой, то этот индекс можно опустить.

Число в этой системе счисления записывается как сумма единиц, двоек, четвёрок, восьмёрок и так далее. То есть веса соседних разрядов различаются в два раза. Точно также записываются и числа, меньшие единицы. В этом случае разряды числа будут называться как половины, четверти или восьмые доли единицы.

Рассмотрим пример записи двоичного числа:

A₂=101110,101₂=1*2⁵+0*2⁴+1*2³+1*2² +1*2¹+0*2⁰+1*2^-1+0*2^-2+1*2^-3=32₁₀+8₁₀+4₁₀+2₁₀+0,5₁₀+0,125₁₀=46,625₁₀

При записи во второй строке примера десятичных эквивалентов двоичных разрядов мы не стали записывать степени двойки, которые умножаются на ноль, так как это привело бы только к загромождению формулы и, как следствие, затруднение понимания материала.

Недостатком двоичной системы счисления можно считать большое количество разрядов, требующихся для записи чисел. В качестве преимущества этой системы счисления можно назвать простоту выполнения арифметических действий, которые будут рассмотрены позднее.

Восьмеричная система счисления Основание этой системы счисления p равно восьми. Восьмеричную систему счисления можно рассматривать как более короткий вариант записи двоичных чисел, так как число восемь является степенью числа два. В этой системе счисления используется восемь цифр. Чтобы не выдумывать новых символов для обозначения цифр, в восьмеричной системе счисления были использованы символы десятичных цифр 0, 1, 2, 3, 4, 5, 6 и 7. Для того чтобы не спутать систему счисления в записи числа используется индекс 8. Если же кроме восьмеричной формы записи чисел не предполагается использования никакой другой, то этот индекс можно опустить.

Число в этой системе счисления записывается как сумма единиц, восьмёрок, шестьдесят четвёрок и так далее. То есть веса соседних разрядов различаются в восемь раз. Точно также записываются и числа, меньшие единицы. В этом случае разряды числа будут называться как восьмые, шестьдесят четвёртые и так далее доли единицы.

Рассмотрим пример записи восьмеричного числа:

A₈=125,46₈=1*8²+2*8¹+5*8⁰+4*8^-1+6*8 ^-2=64₁₀+16₁₀+5₁₀+4₁₀/8₁₀+6₁₀/64₁₀= 85,59375₁₀

Во второй строке приведённого примера фактически осуществлён перевод числа, записанного в восьмеричной форме в десятичное представление того же самого числа. То есть мы фактически рассмотрели один из способов преобразования чисел из одной формы представления в другую.

Так как в формуле используются простые дроби, то возможен вариант, что точный перевод из одной формы представления в другую становится невозможным. В этом случае ограничиваются заданным количеством дробных разрядов.

Шестнадцатеричная система счисления Основание этой системы счисления p равно шестнадцати. Эту систему счисления можно считать ещё одним вариантом записи двоичного числа. В этой системе счисления используется шестнадцать цифр. Здесь уже не хватает десяти цифр, поэтому приходится придумать недостающие шесть цифр.

Для обозначения этих цифр можно воспользоваться первыми буквами латинского алфавита. При записи шестнадцатеричного числа неважно буквы верхнего или нижнего регистра будут использоваться в качестве цифр. В качестве цифр в шестнадцатеричной системе используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Так как здесь появляются новые цифры, то приведём таблицу соответствия этих цифр десятичным значениям.

Шестнадцатеричная цифра	Десятичный эквивалент
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
A	10
B	11
C	12
D	13
E	14
F	15

Число в этой системе счисления записывается как сумма единиц, чисел шестнадцать, двести пятьдесят шесть и так далее. То есть веса соседних разрядов различаются в шестнадцать раз. Точно также записываются и числа, меньшие единицы. В этом случае разряды числа будут называться как шестнадцатые, двести пятьдесят шестые и так далее доли единицы.

Рассмотрим пример записи шестнадцатеричного числа:

A₁₆=2AF,C4₁₆=2*16²+10*16¹+15*16⁰+12*16^-1+4*16 ^-2=512₁₀+160₁₀+15₁₀+12₁₀/16₁₀+4₁₀/254₁₀= 687,765625₁₀

Из приведённых примеров записи чисел в различных системах счисления вполне очевидно, что для записи одного и того же числа с одинаковой точностью в разных системах счисления требуется различное количество разрядов. Чем больше основание системы счисления, тем меньшее количество разрядов требуется для записи одного и того же числа.

13. Арифметические операции над целыми двоичными числами.

Сложение Вообще, сложение чаще всего заменяет все операции в ЭВМ, в том числе и вычитание, поэтому этот пункт будет самым большим, ибо нам надо разобрать все возможные случаи. Для примера будем брать 2 числа: A и B, которые будут менять свои значения в зависимости от примера. Стоит заметить, что все операции сложения чаще всего ведутся в обратных кодах. Не забываем, что у положительного числа все коды одинаковы.

Основные принципы сложения:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 0

1 + 1 = 10

В последнем случае при сложении в столбик мы пишем 0, а 1 запоминаем. Все, как и в обычном сложении.