
- •1.Моделированьепроцесса решения.
- •2. Формализация процесса решения задачи.
- •1) Поиск решения эквивалентной задачи.
- •3.Интуитивное понятие алгоритма.
- •4.Основные свойства алгоритма.
- •5.Взаимосвязь между набором элементарных операций и исполнителем алгоритма.
- •6. Способы изображения алгоритма.
- •7.Введение в язык Си: истоки, парадигма программирования (отношение между набором алгоритмов и набором данных в программах).
- •8.Структура программ на языке Си. Директива процессора, комментарии.
- •11. Описание переменной: имя переменной; строчные и прописные буквы в идентификаторах, задание начального значения (инициализация).
- •15.Преобразование операндов в арифметических выражениях.
- •16.Сложние объявления и элементы объявления.
- •17.Указатели (2 категории).
- •19. Оператор постфиксного увеличения/ уменьшения.
- •20. Оператор префиксного увеличения/ уменьшения.
- •21. Простой оператор присваивания.
- •22. Составные операторы присвоения.
- •23. Условный оператор if.
- •24. Оператор выбора switch.
- •25. Понятие массива, описание массива, размерность массива, размещение в памяти.
- •26. Описание массива имеет вид:
- •27. Массивы символов и литеральные строки.
- •28. Операторы цикла (for, while и do-while) для работы с массивами.
- •29. Многомерные массивы: описание, размещение в памяти, инициализация, обращение к элементам.
- •30. Взаимосвязь массивов и указателей. Описание указателя.
- •32. Указатель типа void*. Преобразование указателя операцией приведения типа.
- •33. Доступ к переменным через указатели: операция & и операция *.
- •37.Синтаксис объявления (--заголовка, --прототипа ) функции. Оператор return
- •38. Понятие формальных параметров и фактических аргументов (при вызове ф-ции). Переменное число аргументов или аргументы с изменяющимися типами (многоточие).
- •39. Указатель на функцию
- •40. Перегрузка функций
- •41. Итерпритация сложных описаний изнутри наружу.
1.Моделированьепроцесса решения.
Переменная:
1) имя 2) тип 3) адрес 4) значение
Х – исходная информация
У – выходная (искомая) информация
Метод прямого поиска:




 Х →У
Х →У
 →
→
 →
→
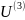 … →
… →
 = У
= У
Метод обратного поиска:
Y


 →
→
 … →
… →
 = Х (S<i)
= Х (S<i)
Метод комбинированного поиска:
 →
→

Близость задач (их эквивалентности: новых и старых):
1) Тождественные задачи – если у двух задач совпадают по значению все исходные и искомые величины.
Х1≡Х2 У1≡У2
2) Эквивалентные задачи – задачи которые совпадают с точностью до значений и обозначений переменных в допустимом классе исходных данных.
Например: решение квадратного уравнения.
3) Однотипные задачи – задачи к которым можно применить один и тот же метод решения.
Методы построения алгоритма решения:
1) Поиск решения эквивалентной задачи.
2)Разбиение задачи на подзадачи (известного типа) и установление связи между ними.
3) Введение вспомогательных параметров.
2. Формализация процесса решения задачи.
От понимания текста задания и словесного описания задачи необходимо перейти к выбору формальной схемы ее решения.
Когда условие задачи стало предельно ясным, но идей, как свести ее к математической или алгоритмической формулировке, еще не возникло, необходимо попытаться упростить задачу и начать ее решение с рассмотрения самых простых случаев. (ручной способ)
Сложность этапа формализации – существует несколько подходов к решению одной и той же задачи. Главное, увидеть хотя бы один из них и определить, как его можно реализовать.
В силу множественности решений не факт, что мы выбрали правильный или приемлемый путь. Но это можно выяснить только на последующих этапах. Поэтому не исключено, что после неудач в построении алгоритма нам придется опять возвратиться на этот этап.
Методы построения алгоритма решения:
1) Поиск решения эквивалентной задачи.
2)Разбиение задачи на подзадачи (известного типа) и установление связи между ними.
3) Введение вспомогательных параметров.
3.Интуитивное понятие алгоритма.
Алгоритм – последовательность действий, известных исполнителю, направленных на получения определенного результата за конечное число шагов.
4.Основные свойства алгоритма.
1. Свойство детерминированности - алгоритм должен быть разбит на отдельные шаги, на каждом шагу мы получаем промежуточные данные, начиная от исходных, которые являются исходными для следующих шагов.
2. Свойство дискретности – алгоритм представляется в виде конечной последовательности шагов.
3. Каждый шаг алгоритма должен быть элементарным для исполнителя.
4. Свойство определенности алгоритма – действия, выполняемые на каждом шаге алгоритма однозначны, и результат определяется значениями, полученными на предыдущих шагах.
5. Свойство массовости алгоритма определяет допустимые исходные данные.
6. Свойство конечности – количество шагов в алгоритме должно быть конечным.
Сам алгоритм и исходные данные представляются исполнителю в некоторой форме. Дается на двух языках: алгоритмическом(на котором сформирован сам алгоритм), и языке спецификаций(данных, операндов, на котором описаны данные для алгоритма).
