- •1.Случ-й экспер-т. Пространство элементар-х исходов. Дискретные и непрерывные пространства элементар-х исходов. Примеры.
- •2.Случа-е события. Пр-ы. Достоверное, невозможное, противоположное соб-я. Несовместные соб-я. Полная группа соб-й. Пр-ы.
- •3.Случ-е соб-я. Пр-ы. Операции над соб-ми.
- •3 Аксиомы а.Н. Колмогорова
- •5.Классический метод выч-ия вер-ей. Пр-ы.
- •6.Статисти-ий метод вычисления вер-ей. Пр-ы.
- •7.Элементы комбинаторики. Классификация выборок. Пр-ы. Количество перестановок.
- •9.Элементы комби-ки. Неупор-ые выборки. Пр-ы.
- •10.Теор-а сложения вер-ей для 2-х соб-й (общий и частный случаи). Те-а сложения вер-ей для 3-х событий (общий и частный случаи).
- •2)Общий случай для 3-х событий
- •14.Формула полной вероят-и. Формула Байеса.
- •15.Испытания Бернулли. Фор-а Бернулли. Наиболее вероя-е число успехов в фор-е Бернулли.
- •16.Испытания Бернулли. Формула Пуассона.
- •17.Испытания Бернулли. Локальная формула Муавра-Лапласа.
- •18.Испытания Бернулли. Интегральная формула Муавра-Лапласа.
- •19.Случайная величина. Примеры. Дискретные и непрерывные случайные величины.
- •20.Дискретная случ-я величина. Пр-ы. Закон распределения дискретной случ-й величины.
- •21.Непрерывная св Пр-ы. Закон распределения непрерывной св.
- •22.Непрерывная св. Пр-ы. Функция распределения непрерывной св и ее свойства.
- •23.Непрерывная св Пр-ы. Функция плотности непрерывной св и ее свойства.
- •24.Числовые характеристики св Математическое ожидание, дисперсия, среднее квадратичное отклонение, мода, медиана дискретной св.
- •25.Числовые характеристики св. Математич-е ожидание, дисперсия, среднее квадратичное отклонение, мода, медиана непрерывной св
- •26.Числовые характеристики св. Свойства математического ожидания и дисперсии.
- •27.Биномиальный закон распределения. Примеры.
- •28.Закон распределения Пуассона. Примеры. Простейший поток событий.
- •30.Показательный (экспоненциальный) закон распределения. Примеры.
- •31.Нормальный закон распределения. Пр-ы.
- •32.Вычисление вер-и попадания непрерывной св в заданный интервал с помощью функции плотности и функции распределения.
- •34.Предмет и задачи математи-ой статистики. Генеральная и выборочная совокупности.
- •35.Вариационный ряд. Статист-й закон распр-я дискретной св. Столбцовая диаграмма.
- •36.Вариационный ряд. Статистический закон распределения непрерывной св Гистограмма.
- •37.Эмпирическая функция распределения и ее график. Св-ва.
- •38.Точечные оценки числовых характеристик cв. Пр-ы. Свойства оценок: несмещенность, эффективность и состоятельность.
- •39.Точечные оценки числовых характеристик св. Оценки математ-го ожидания, дисперсии, среднего квадратического отклонения. Пр-ы.
- •40.Точечные оценки числовых характеристик св. Оценки среднего квадратического отклонения, медианы, моды (для дискретной и непрерывной случайной величины). Примеры.
- •42.Статис-ая проверка гипотез. Параметрические и непараметрические гипотезы. Вер-ти ошибок 1-го и 2-го родов. Пр-ы.
- •48.Применение метода наименьших квадратов для нахождения оценок параметров уравнения регрессии. Нелинейная регрессионная модель.
- •49.Оценка коэффициента корреляции. Св-ва.
- •50.Проверка значимости кк.
- •51. Коэффициент детерминации и его свойства.
- •52.Проверка значимости кд.
9.Элементы комби-ки. Неупор-ые выборки. Пр-ы.
Основная лемма ком-ки: Из m элем-в 1-й группы а1, а2,.,аn и n элем-в 2-й группы b1,d2,…,dnможно составить ровно mxn упорядоч-ых пар вида (аi, bi)
|
Не упоря-я |
С возвра-м |
Ckn=Ckn+k-1= |
Без возвр-я |
Ckn= |
10.Теор-а сложения вер-ей для 2-х соб-й (общий и частный случаи). Те-а сложения вер-ей для 3-х событий (общий и частный случаи).
1)Общий(совмест-е):Р объединения 2-х соб-й А и В =∑ вер-й этих соб-й минус вер-ь персечения.
Р(AB)=Р(А)+Р(В)-В(AB)
Частный(несовм-е): если соб-я А и В не совм-е,
Р(AB)=Р(А) Р(В)
2)Общий случай для 3-х событий
Р(АВС)=Р(А)+Р(В)+Р(С)-Р(AB)-Р(AС)-Р(ВС)+( ABС)
Частный случай для 3-х соб-й
Р(АВ, С)=Р(А)+Р(В)+Р(С)
11.Тео-а сложения вер-ей для 2-х соб-й (общий и частный случаи). Теор-а сложения вер-ей для конечного числа несовместных соб-й.
1)Общий(совмест-е):Р объединения 2-х соб-й А и В =∑ вер-й этих соб-й минус вер-ь персечения.
Р(AB)=Р(А)+Р(В)-В(AB)
Частный(несовм-е): если соб-я А и В не совм-е,
Р(AB)=Р(А) Р(В)
Для попарно несовм-х событий А1, А2,…,Аn..
Р(А1А2, …Аn)=Р(А1)+Р(А2)+…+Р(Аn)
12.Тео-а умнож-я вер-ей 2-х событий. Условная вер-ть. Зависимые и независимые соб-я.
Условная вер-ть-вер-ть соб-я А, вычисленная при условии, что соб-е В произошло.
P(AB) = P(B)P(A|B) = P(A)P(B|A)
и называют теоремой умножения вероятностей.
Частный:если соб. А и В явл-я не завис-е то
P(AB)=Р(А)Р(В)
Различают соб-я зависимые и независимые. 2 соб-я наз-я независимыми, если появление одного из них не изменяет вер-ь появления другого. П-р, Монета брошена 2 р-а. Вер-ть появления "герба" в 1-м испытании не зависит от появления или не появления "герба" во 2-ь испытании. Несколько соб-й наз-я независимыми в совок-ти, если любое из них не зависит от любого другого соб-я и от любой комбинации остальных.
2 соб-я наз-я зависимыми, если вер-ь одного из них зависит от наступления или не наступления другого. в случае зависимых соб-й вводится понятие условной вер-ти соб-я. Условной вероятностью Р(А/В) соб-я А наз-я вер-ь соб-я А, вычисленная при условии, что соб-е В произошло.
13.Тео-а умножения 2-х соб-й. Тео-а умножения вер-ей для конечного числа соб-й (общий и частный случаи).
P(AB) = P(B)P(A|B) = P(A)P(B|A)
и называют теоремой умножения вероятностей.
Частный:если соб. А и В явл-я не завис-е то
P(AB)=Р(А)Р(В)
Для конечного числа:
Р(А1А2, …Аn)=Р(А1)Р(А2)…Р(Аn)
Теор-а умно-я для 3-х со-й:
Р(АВ, С)=Р(А)Р(В/А)Р(С/АВ)
14.Формула полной вероят-и. Формула Байеса.
Соб-е Н1, Н2,,Нn наз-я гипотезами, если они яв-я попарно несовмес-е(Н1Н2=) и их объединение есть достоверное соб-е (Н1Н2,,Нn=)
Если соб-е А может произойти одновр-но только с одной из гипотиз Нi при этом вер-ть соб-я А зависит от того какая из гипо-з наступила, то имеет место фор-а полной вер-ти:
Р(А)=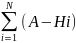
P(A)=P(H1)P(A|H1)+P(H2)P(A|H2)+…+P(Hn)P(A|Hn)
Если известно, что в результате опыта произошло событие A,и мы хотим пересчитать вер-ть гип-з исполь-я формула Байеса