§5. Метод интегрирования подстановкой (замена переменной).

Часто интеграл можно значительно упростить, сделав замену переменной. Такой метод интегрирования заключается в том, что при помощи подстановки переменная интегрирования заменяется на функцию от другой независимой переменной.

Пусть нужно найти .

Сделаем замену переменной , где – функция, имеющая непрерывную производную. Тогда .

Получим формулу интегрирования подстановкой:

.

Эта формула также называется формулой замены переменной в неопределенном интеграле. После вычисления интеграла правой части формулы следует вернуться к старой переменной интегрирования x.

Иногда бывает удобнее сделать подстановку в виде . Как это сделать мы увидим далее в процессе решения примеров.

Примеры.

1. Найти

Решение.

Сделаем замену

Тогда , и

Возвращаясь к переменной x, получаем

Можно использовать краткую запись, выделяя замену переменной и выкладки, связанные с ней, вертикальными линиями. Запись данного примера будет выглядеть так:

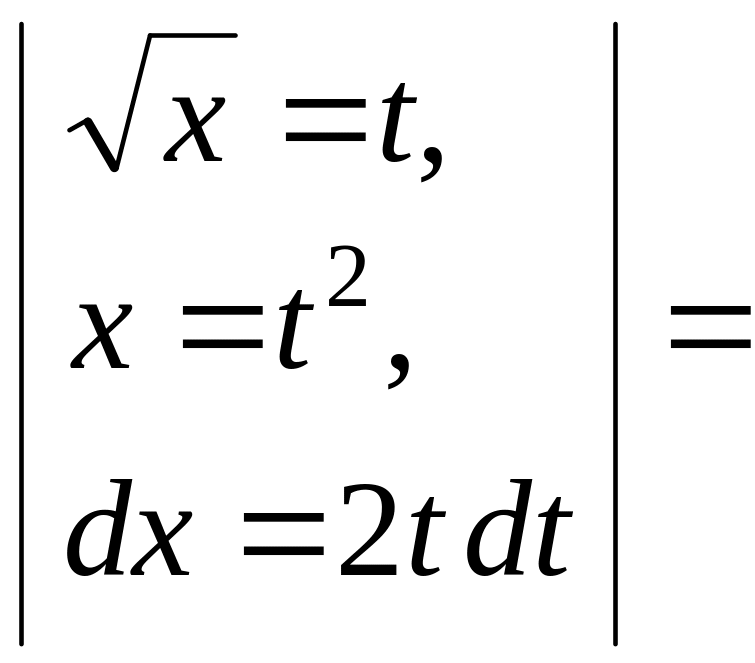
2. Вывести формулу для табличного интеграла

Решение.

Введем новую переменную

Такая подстановка называется подстановкой Л. Эйлера. Выразим переменную x через t. Для этого проделаем следующие выкладки:

Найдем dx:    

Выразим через t:

Подставим dx и под знак интеграла и получим

Замечание. Так как этот интеграл часто встречается в приложениях, а нахождение его трудоемко, мы включили его в основную таблицу интегралов.

3. Найти

Решение.

Сделаем замену . Тогда , .

Теперь нужно вернуться к старой переменной. Получим

4. Решим предыдущий пример другим способом.

Сделаем замену . Тогда и

Применяя тригонометрическую формулу

получим

Следовательно,

.

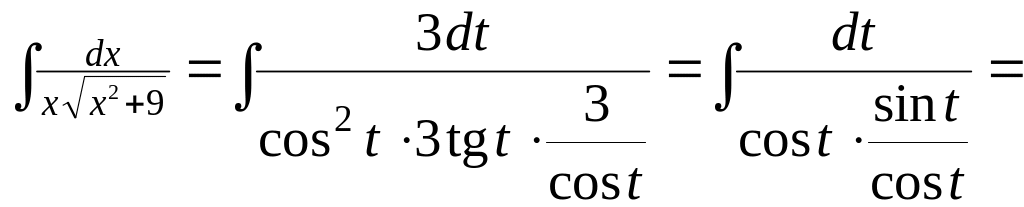
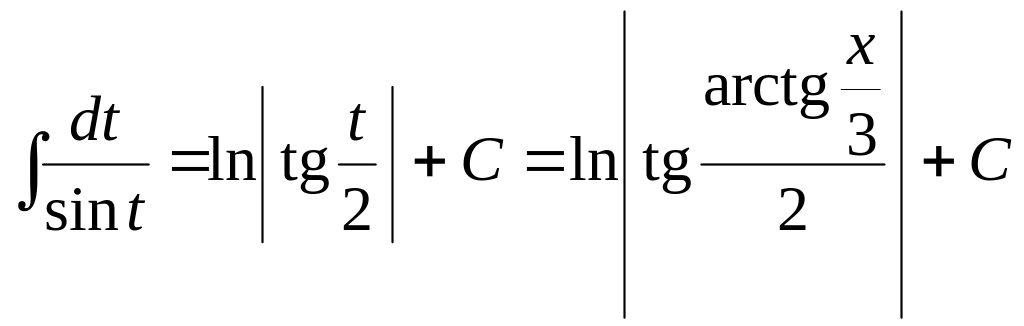Мы видим, что при различных подстановках получены разные по виду результаты. На самом деле можно доказать, что результаты одинаковы.

1. Найти

Решение.

Выделим в знаменателе полный квадрат

и сделаем замену тогда

Примеры для самостоятельного решения

Задание	Ответ	Подстановка
1.
2.
3.		Выделить полный квадрат в подкоренном выражении.
4.
5.
6.
7.
8.
9.

Приложение

Алгебраические выражения

;

;

Cвойства степеней

Логарифмы

( )

,

Тригонометрические функции
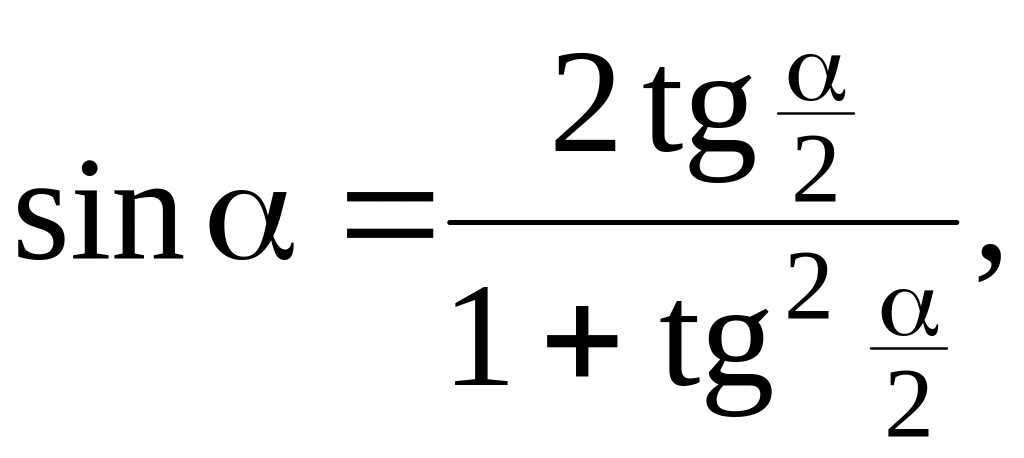
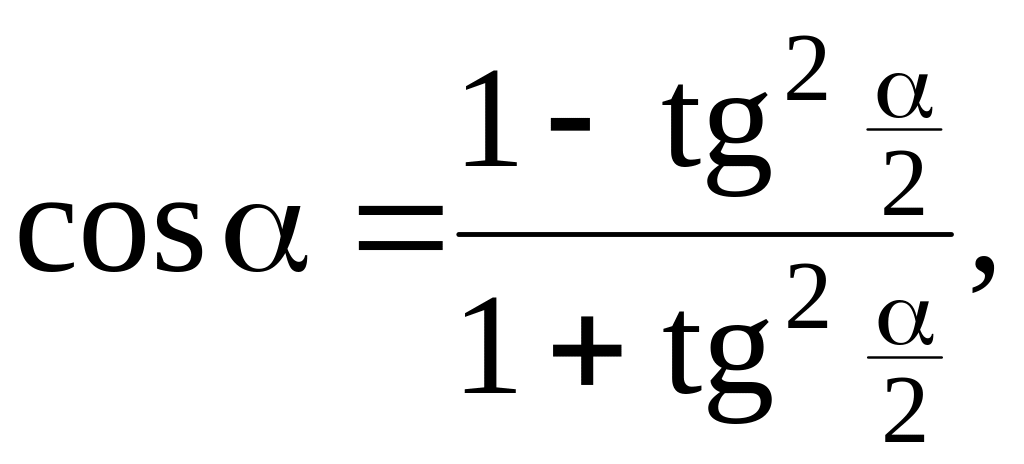