22. Генератриси, їх властивості.

приймає цілі невід’ємні значення.

P( =k)=p_k. , k=0, 1, 2…

Генератриса:

A(s)=Ms^ксі= ^k p_k. |s|<=1

1) A(1)= p_k =1

2)|A(s)|<=1, |A(s)|<= p_k <= p_k =1.

3)A’(1)<=M

A’(s)= * p_k |_s=1 = p_k = M

4)A”(1)= p_k = p_k - p_k =M ² - M

D = M ² – (M )²=A’’(1)+A’(1) – (A’(1))².

5)A(0) = p₀=p( =0).

6) і – незалежні події. A_{ксі+ета}(s)=A_ксі(s) * A_ета(s).

A_{ксі+ета}(s)=Ms^{ксі+ета} = Ms^ксі *s^ета = Ms^ксі*Ms^ета = A_ксі(s)*A_ета(s).

p_k A(s) – бієкція (кожному розподілу відповідає своя генератриса, кожній генератрисі – свій розподіл)

p_k = . A(s) = ^k* = = = .

A_{ксі+ета}(s)=A(s) _ксі *A _ета(s) = * = .

23. Характеристична функція.

Під характеристичною функцією розуміють математичне сподівання випадкової величини : ,де  — дійсний параметр.

Дискретний розподіл: p(x) (e в степені itx)

Неперервний розподіл: .

Рівномірний розподіл на відрізку [a,b]:

= |^b_a= ( ).

Рівномірний розподіл на відрізку [-1, 1]: .

x_k -1 1

P_k ½ ½

=

- біноміальний розподіл

= .

A(s)=

s= - генератриса стає характеристичною функцією

A(s) =

=

Властивості:

1) . |M < M| |

.

2)| | = |

3) . , > 0

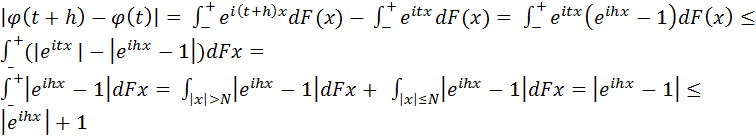=1+1=2

I₁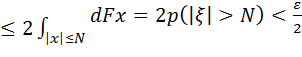

I₂

I₁ + I₂ =

4) (//над cпряжений//)

5) – дод визначена функція

6) - незалежні

(t) = M * M =M =

7) , a, b = const

8)M |

(t)=

(t)=

(0)=

(t)= (0)=

24. Перша теорема Хелі

Лема: Для того, щоб послідовність F₁(x), F₂(x)…F_n(x) слабо збігалась до 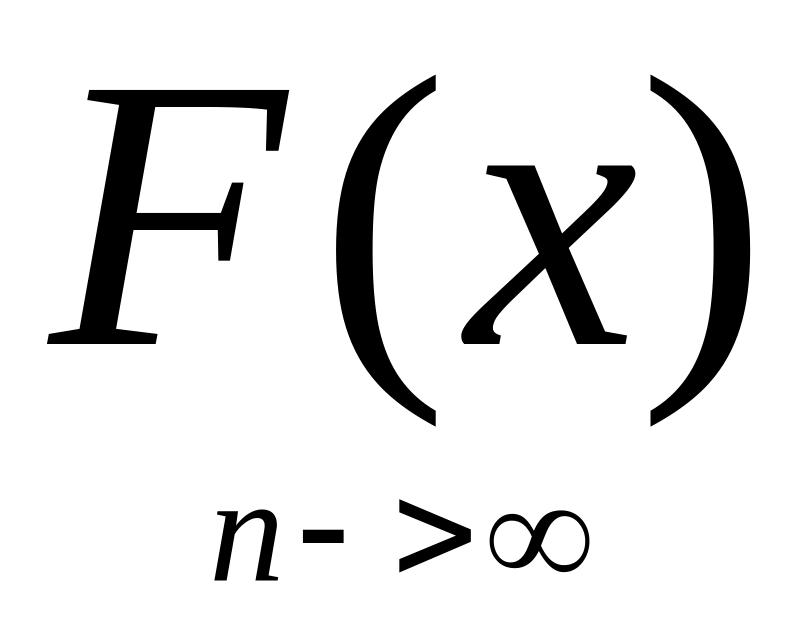достатньо збіжності цієї послідовності на всюди щільній множині D. D – яку б точку із R ми не взяли, якмй би окіл (x- ,x+ ) не взяли, точка d завжди буде потрапляти в D.

Доведення: х – точка неперервності F(x). D={x₁,x₂…} ,x₁<=x<=x₂

Fn(x1)<=Fn(x)<=Fn(x2)

lim F_n(x)<=F_n(x)

x₁->x-0; x₂->x+0

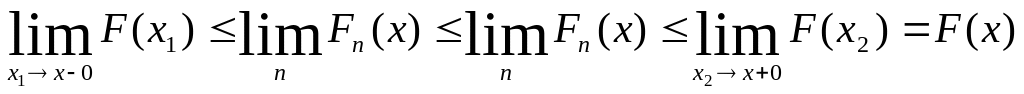
1 теорема Хелля

З будь-якої послідовності функцій розпроділу F₁(x), F₂(x)…F_n(x) можна виділити підпослідовність, яка буде слабо збігатися до деякої функції F(x).

D={x₁,x₂…}

F₁(x₁), F₂(x₁)…F_n(x₁)

F_1n(x₁)F(x₁) n∞

F₁₁(x₂), F₁₂(x₂)…F_1n(x₂)

F_2n(x₂)F(x₂)

F_kn(x₂)F(x₂)

Діагональна процедура

F₁₁(x), F₂₂(x)…F_kk(x)

F_nn(x)F(x)

25. Друга Теорема Хеллі

Нехай f(x) неперервна на [a,b] ,f(x) є С_[a,b] якщо F_n(x) F(x) х-точка неперервності

тоді

Доведення: f(x),(a,b)

Оскільки, , , та в силу збіжності F_n(x) F(x), де x₀,x₁…x_N – точки неперервності.

При достатньо великих n буде виконуватись ,

а отже і ,де М – максимум модуля f(x)

Отже,

Третя теорема Хеллі

Якщо f(x)- неперервна на і F_n(x) F(x)

то

26. Теорема неперервності

Теорема неперервності для характеристичних функцій.

Пряма теорема

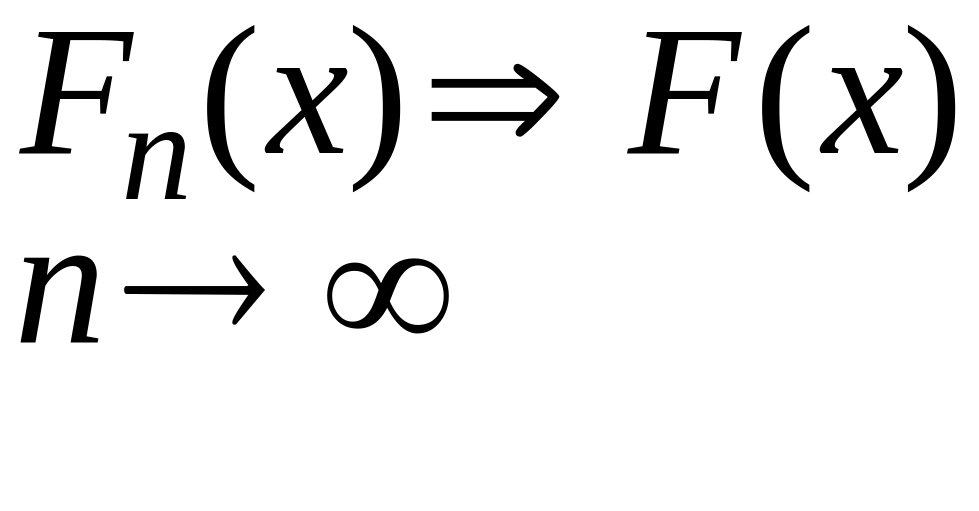
тоді

Обернена теорема

Якщо , тоді при цьому буде її характеристичною функцією.

Наслідок теореми неперервності

Теорема Пуасона

- загальна кількість успіхів

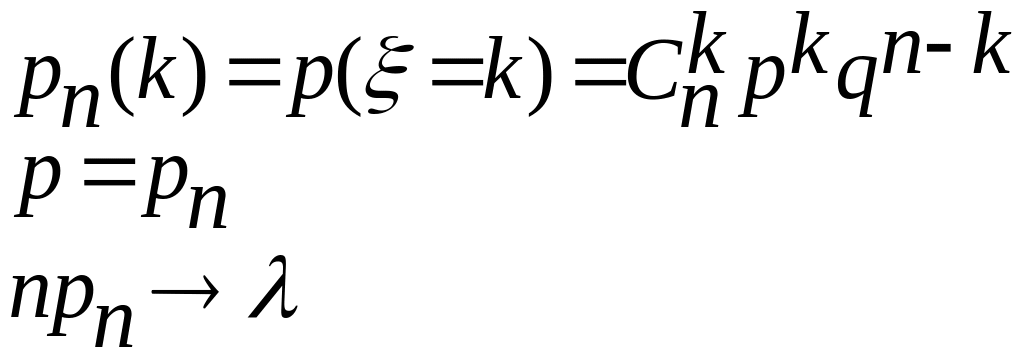
тоді

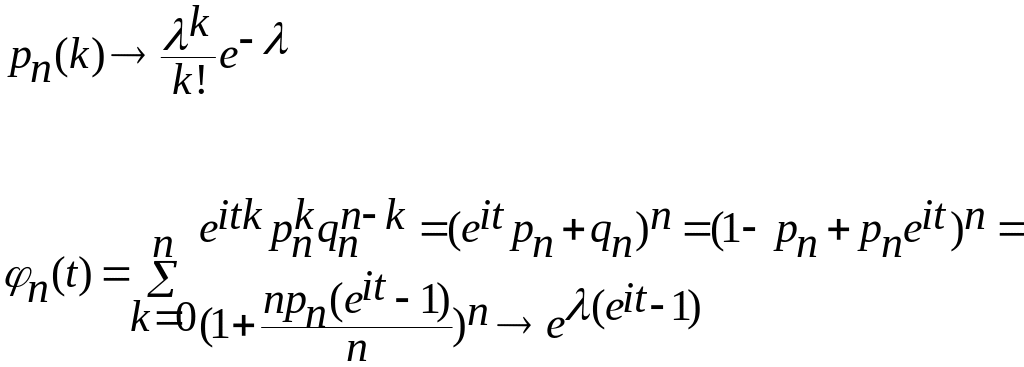
• характеристична функція Пуасона