13.Біноміальний, геометричний та Пуассонівський розподіли. Їх характеристика.

1) Біноміальний розподіл. (Схема Бернулі)

n- нехалежних розподілів

2 результати: - успіх(У) p

-невдача(Н) q

q=1-p p+q=1

- загальна к-сть усіх успіхів; є{0,1,2,…,n}

k- У; (n-k) – Н;

; ;

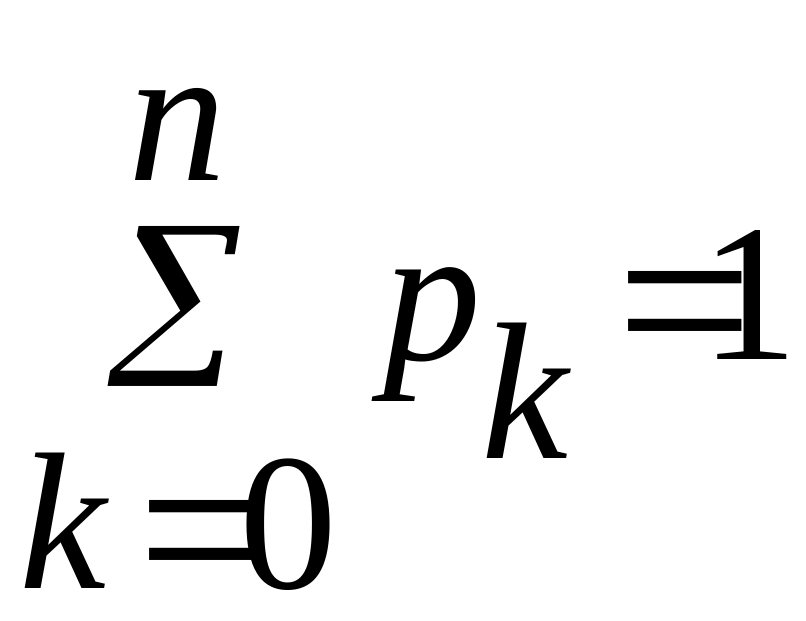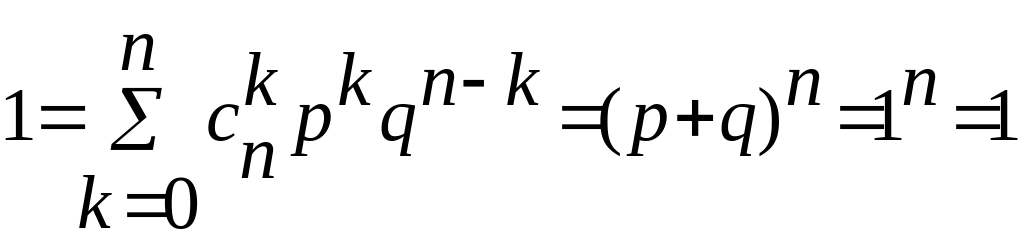2) Геометричний розподіл.

У – к-сть експериментів, що проводяться до першого успіху

Н – к-сть невдач

3) Пуассонівський розподіл.

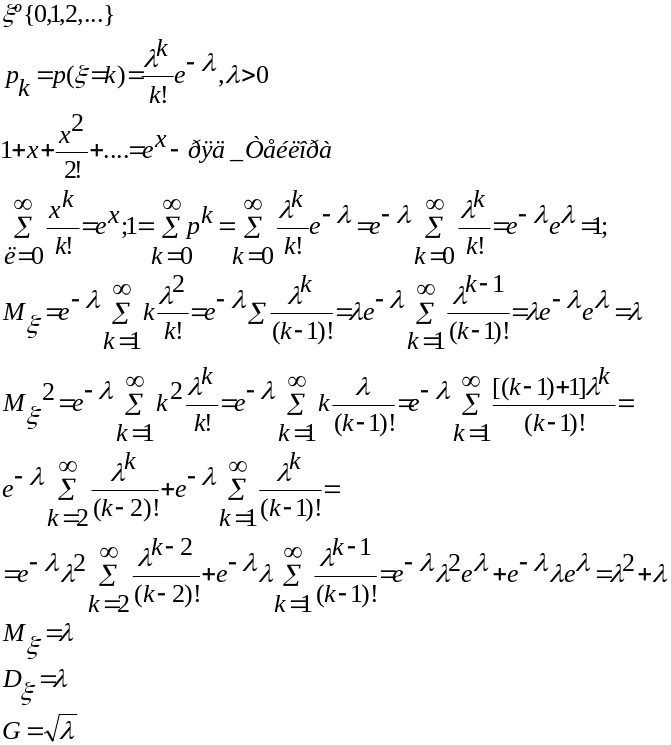
14. Схема Бернулі. Локальна теорема Муавра-Лапласа

1)Схема Бернулі(Біноміальний розподіл)

n – кількість незалежних випробувань

У – успіх. p 0≤p≤1

Н – невдача. q=1-p p+q=1

ξ – загальна кількість успіхів в n-експериментах

ξ є{0,1,2…n}

1. математичне сподівання

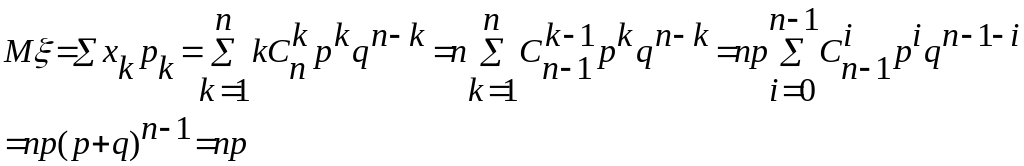
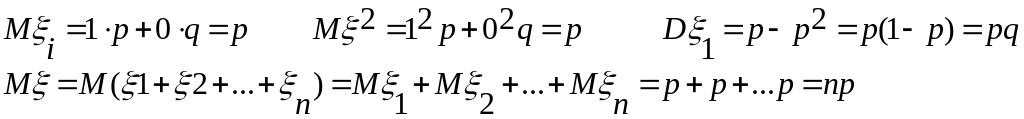
2. Дисперсія

Формули:

2) Локальна теорема Муавра-Лапласа

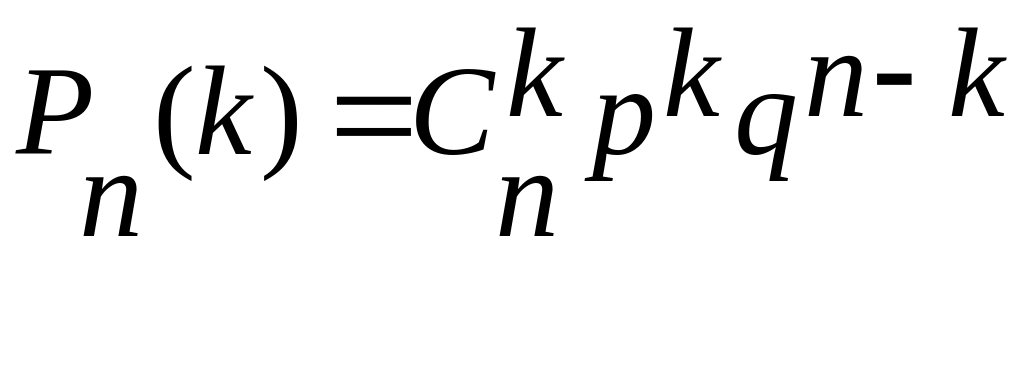
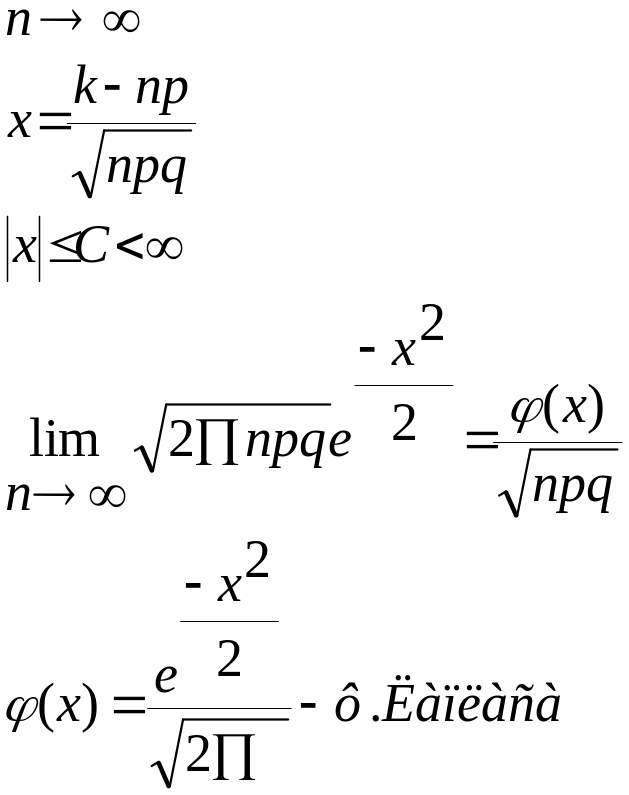
Доведення

Ф-ла Стірлінга: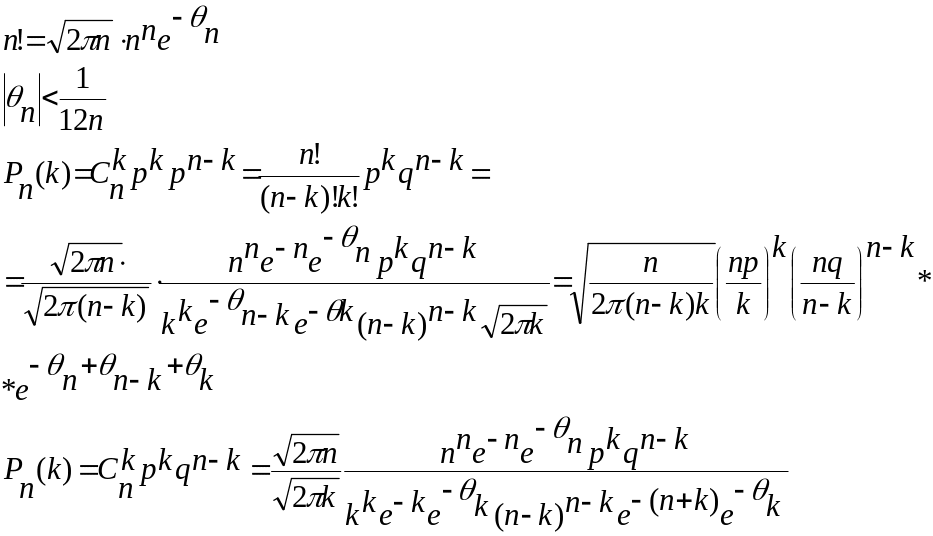

x≤C<+∞

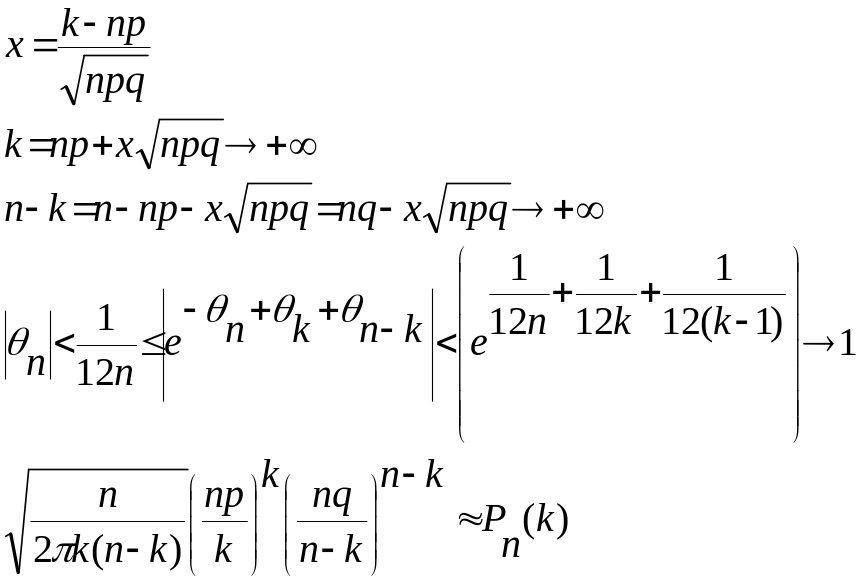
1.

2.

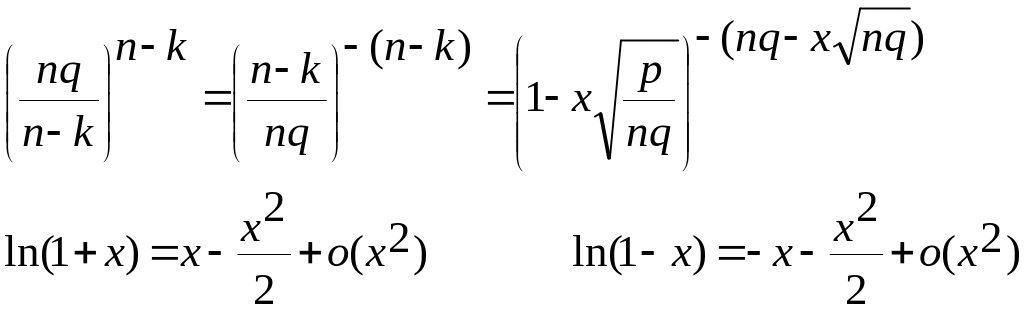
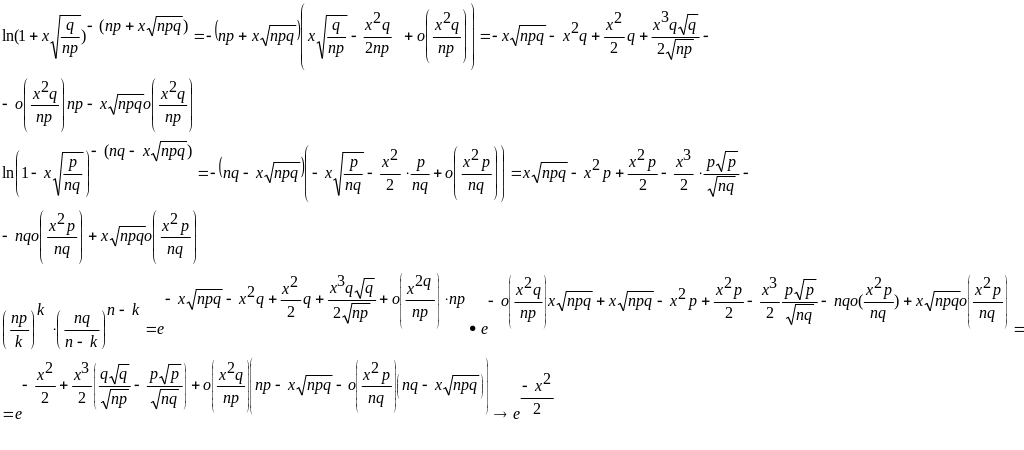
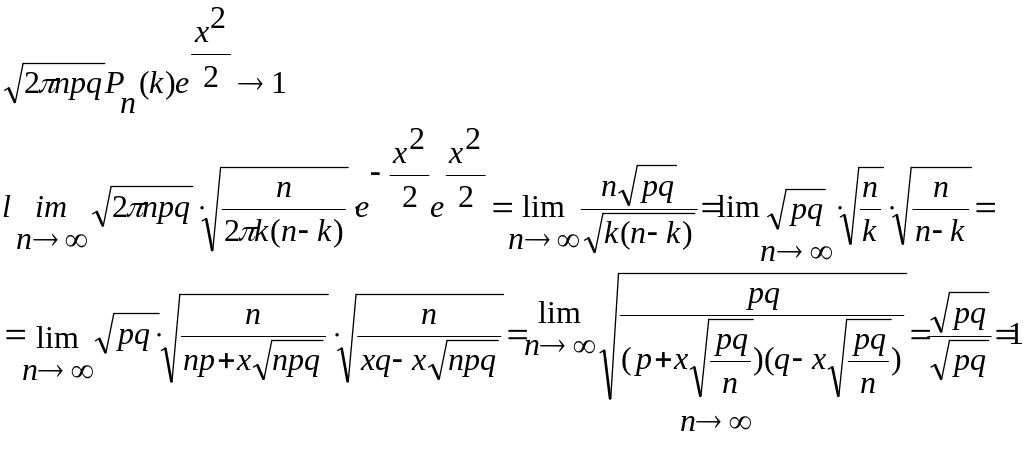
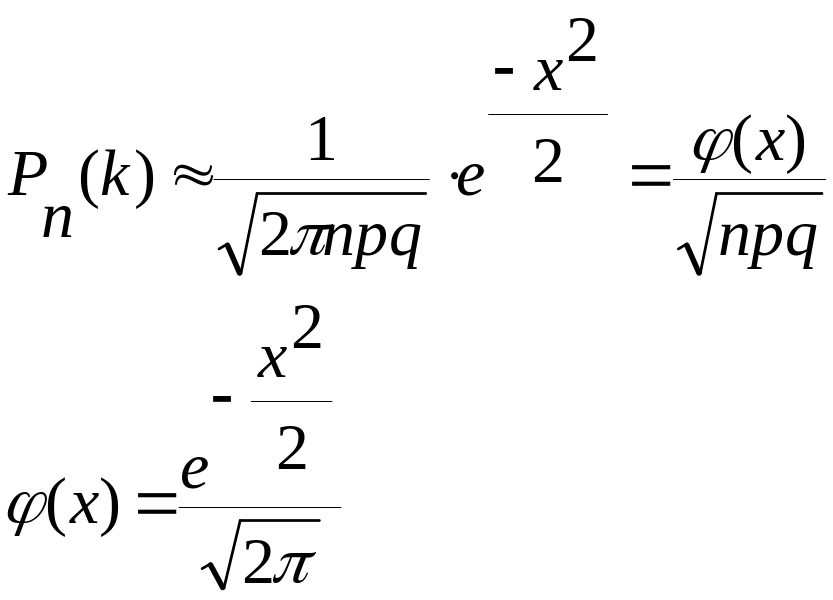
15. Загальне означення випадкової величини

Нехай — ймовірнісний простір. Випадковою величиною називається функція (w) на , яка вимірна відносно -алгебри , тобто така функція, коли при кожному дійсному x

{w : (w) < x} .

Функцією розподілу випадкової величини (w) називається функція

F(x ) = P{w : (w) < x}.

Функція розподілу F(х) має властивості: а) неперервна зліва; б) неcпадна на ; в) F( ) =0, F ( ) = 1.

Для кожної функції F (x), що має ці властивості, можна побудувати ймовірнісний простір

і випадкову величину (w) на ньому, яка має функцією розподілу F(х).

Якщо F (х) — функція розподілу випадкової величини , то

P{a<=x<b}=F(b)–F(a), (a < b).

16. Функція розподілу, щільність випадкових величин.

Випадковою величиною називається функція (w) на , яка вимірна відносно -алгебри , тобто така функція, коли при кожному дійсному x {w : wx} , де (, , P)- ймовірнісний простір.

Функцію аргументу х, що визначає ймовірність випадкової події (Х < x), називають функцією розподілу ймовірностей:

Fx P{w : wx}.

Н априклад, F(5)=P(X < 5) означає, що в результаті експерименту випадкова величина Х (дискретна чи неперервна) може набути значення, яке міститься ліворуч від х = 5, що ілюструє рис.

Властивості функції розподілу F(x):

1. 0 ≤ F(x) ≤ 1

2. F(x) є неспадною функцією, тобто: F(x2) ≤ F(x1), якщо x2 > x1

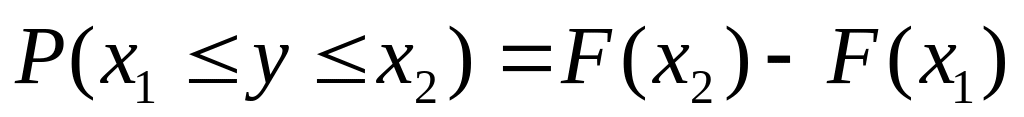3. ,(a<b)

4. F(x) – неперервна зліва

5. F(x) –неспадна a<b; F(a) ≤F(b) P(a≤ 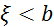)=F(b)-F(a)>0; F(b)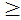 F(a)

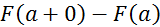6. a-т. Неперервності.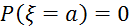

7.

Для кожної функції F (x), що має ці властивості, можна побудувати ймовірнісний простір (, , Р) і випадкову величину (w) на ньому, яка має функцією розподілу F(х).

Щільність розподілу випадкової величини .

Якщо функцію розподілу F(x) випадкової величини можна подати у вигляді

то кажуть, що випадкова величина має щільність розподілу p(x), і таку випадкову величину називають неперервною.

Майже при всіх x виконується рівність F`(x) = p(x). Щільність розподілу p(x) — невід'ємна функція і

Виконується рівність:

Властивості щільності:

1. ;

2. 

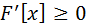
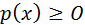
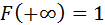
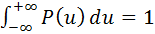
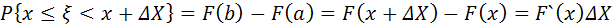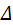3. +O( X)