9. Дискретні випадкові величини. Їх характеристики.

Нехай (Ω, ζ, Р) — ймовірнісний простір. Тоді задається функція, де кожному наслідку відповідає своє значення. w x.

Випадкова величина – вимірна функція ξ(w) на Ω, яка відображає простір елементарних подій на числову вісь. Якщо ВВ приймає дискретну величину значень, то вона дискретна.

Ω {x1,x2,….,xn} p_i=P{w: ξ(w)=x_i} i=1,2,3…

Власт. 0< p_i ≤ 1 E p_i = 1

Розподіл дискретної випадкової величини. Нехай ξ(w) — дискретна випадкова величина, яка набуває значення x1, ..., x i,....

Набір чисел P{w: ξ (w)=xi}=pi (i=1, 2,....) називають розподілом випадкової величини ξ. pi≥0,

^{= 1}.

Часто розподіл випадкової величини подають у вигляді таблиці, в якій

перераховуються значення випадкової величини разом з відповідними ймовірностями:

Значення	x1	…	xi	…
Ймовірність	p1	…	pi	…

Функція розподілу випадкової величини ξ(w) визначається рівністю:

^{P{w: ξ(w)<x}=}

Сумісний розподіл випадкових величин. Нехай ξ(w) — дискретна величина, що набуває значень x1, x2, …, xi, …, η(w) — дискретна величина, що набуває значень y1, y2, …, yj, ….

Набір чисел P{w : ξ(w) = xi, η (w) = yj }=pij, (i =1,2…;j = 1,2…) називається сумісним розподілом випадкових величин ξ та η. Справджуються такі твердження:

^{а) pij≥0 , = 1}

б) ^{= pi, =qj ,} де {рi} — розподіл ξ(w), {qj} — розподіл η(w).

Незалежні випадкові величини. Випадкові величини ξ та η називаються незалежними, якщо для будь-яких i та j

P{ ξ(w) = xi , η(w) = yj } = P{ξ(w) = xi } P{η(w) = yj }.

10. Математичне сподівання (середнє ймовірнісне значення)

ξ	х1	…	хn
	р1	…	рn

= х1 р1+ … + хn рn = ;

Приклад:

_{ξ – очки на першому кубику}

xi	1	2	3	4	5	6
pi

Властивосты математичного сподівання:

1)математичне сподівання є константним

xi	C
pi	1

2)

3)

;

4)

;

5)

6)для незалежних випадкових величин

7)

11. Дисперсія випадкових величин. Властивості.

Дисперсією випадкової величини називається математичне сподівання квадрата відхилення цієї величини. Дисперсія характеризує розсіювання випадкової величини відносно свого математичного сподівання.

_або

_{Доведення:}

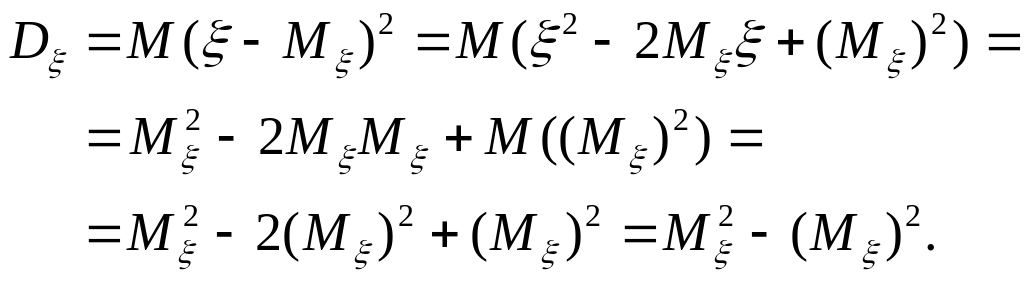
Для дискретної випадкової величини дисперсія:

Для неперервної:

Якщо  [а; b], то

Властивості дисперсії

1.

2. Якщо С — стала величина, то

.

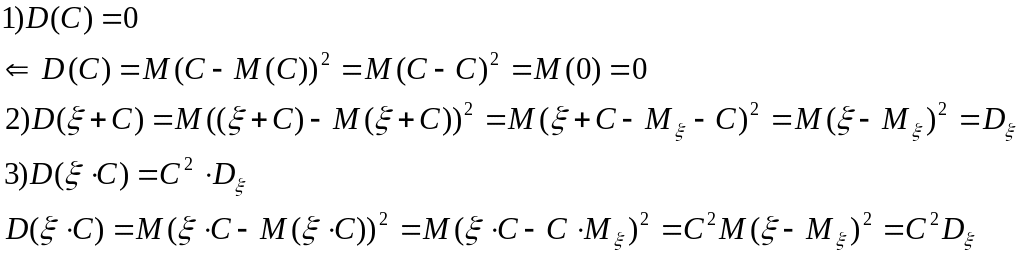3. Якщо і - незалежні випадкові величини, то

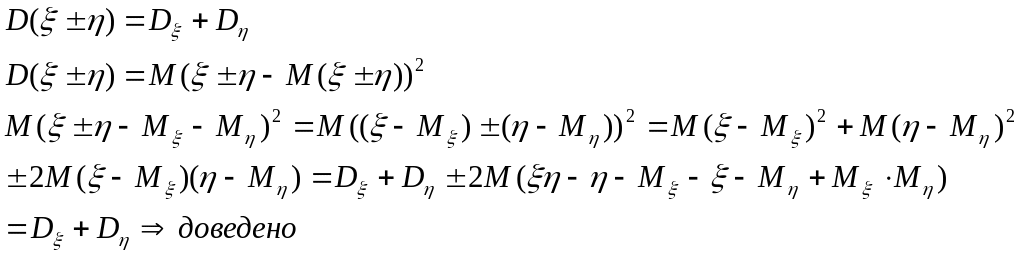
12. Коефіцієнт кореляції випадкових величин

Коефіцієнт кореляції – міра залежності випадкових величин.

1. і - незалежні, ρ=0. 2. | ρ |≤1.

Доведення: = 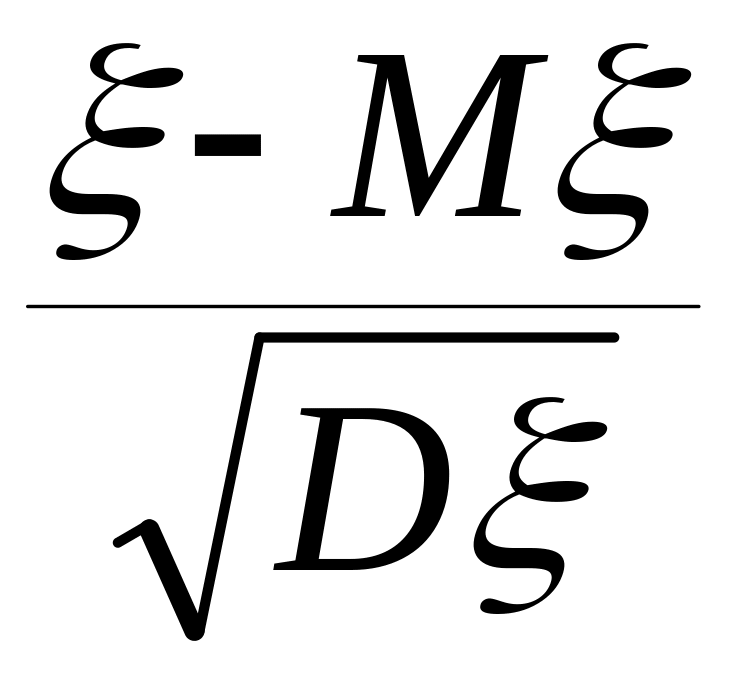- стандартизована випадкова величина

, .

, .

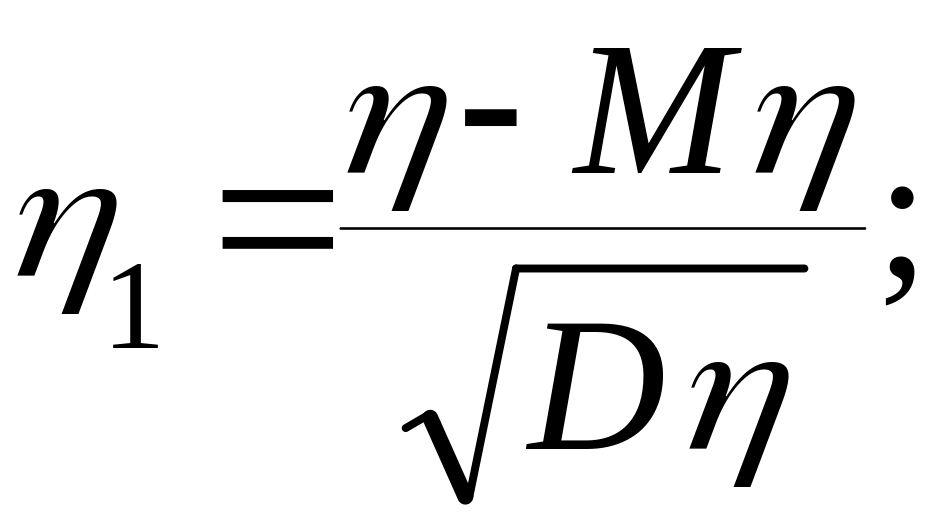
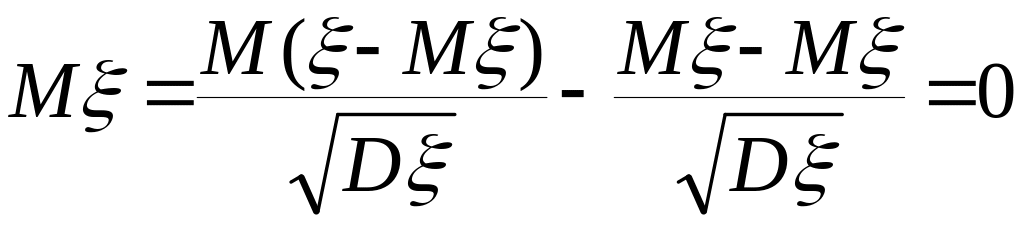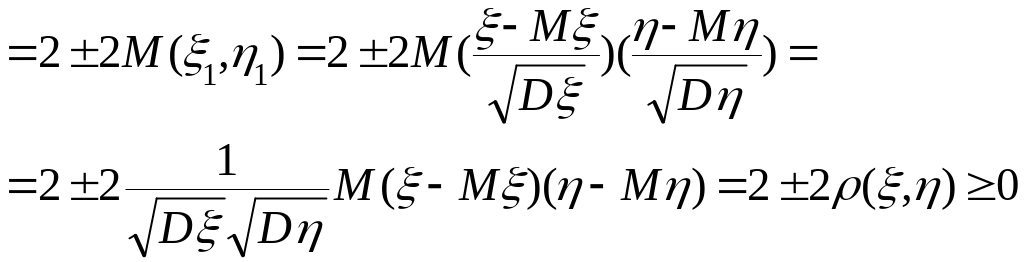
або .

3. | |=1

=1, a>0; =-1, a<0

a)

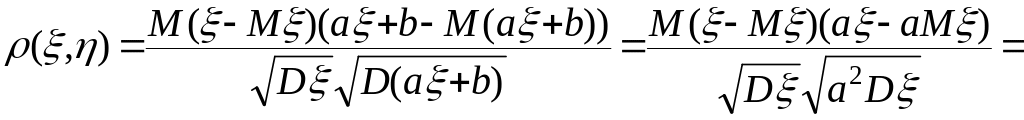
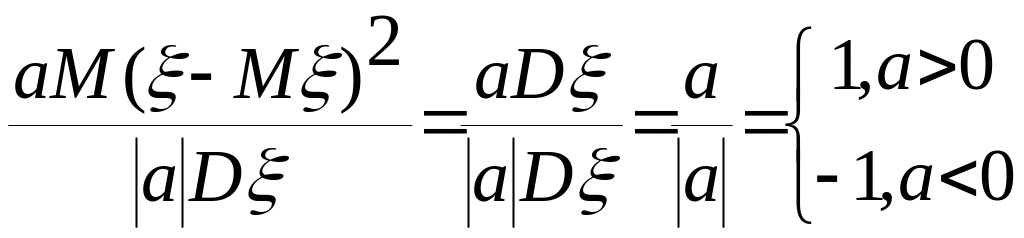
б) ,

, ,

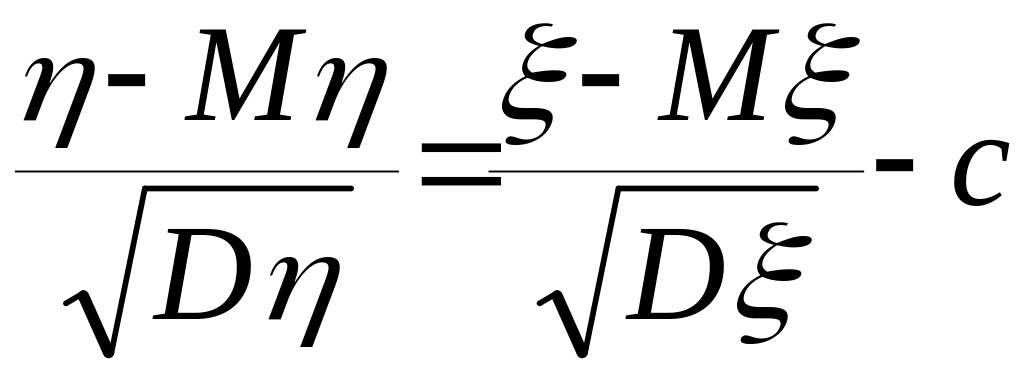
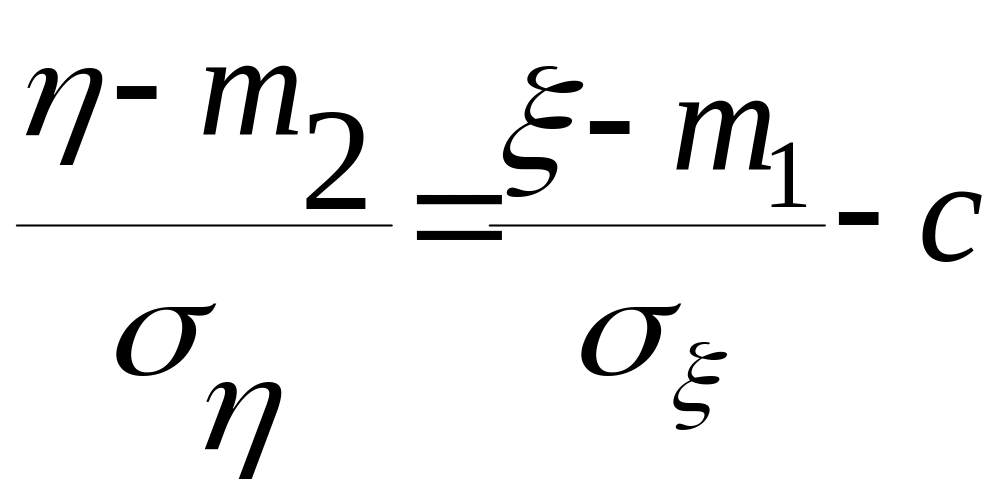
| | 1 – тим сильніша залежність >1 – позитивний звязок (залежність) <0 -

Зауваження: з того, що ρ=0 не впливає незалежність випадкових величин.)