7.5. Условия согласования источника сигнала с нагрузкой

Обычно рассматривают два условия (режима) согласования:

1) получение на нагрузке максимальной амплитуды напряжения – это условие максимального к.п.д. по направлению;

2) условие согласования, при котором на нагрузке выделяется максимальная мощность – условие согласования по мощности.

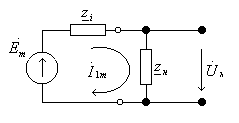- внутренне сопротивление источника э.д.с.,

;

- сопротивление нагрузки,

Установим условие первого режима согласования, т.е. получения на нагрузке максимального напряжения. Запишим выражения для выходного напряжения

. Из него следует, что U_н → max_, когда z_н ›› Z_i

Такой режим согласования используют в энергетических установках. В этом случае, напряжение выделяемое на нагрузке, а, следовательно, и к.п.д. цепи максимально.

Установим условие, второго режима согласования, когда на нагрузке происходит выделение максимальной мощности.

Мощность выделяется на резистивной составляющей Rн сопротивления нагрузки Zн. Это активная мощность, она определяется из выражения

.

Найдем амплитуду тока I_m. Сначала запишем выражение для комплексной амплитуды тока

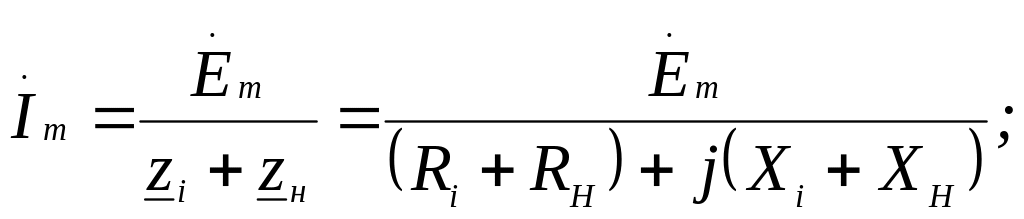
а затем найдем модуль комплексной амплитуды. Это и будет амплитудой тока

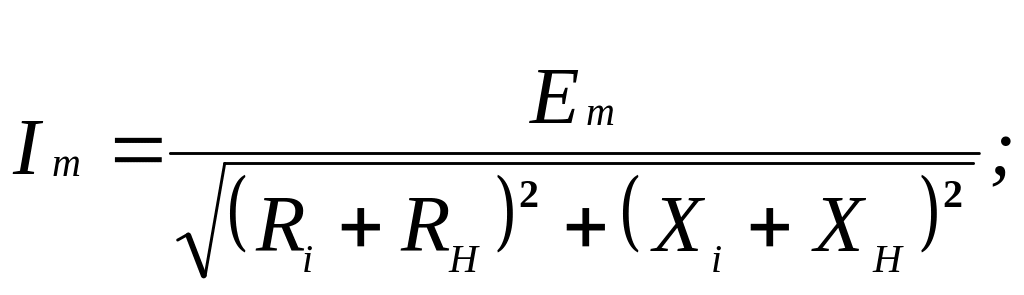
Подставим ток в исходное выражение, получим активную мощность выделяемую в нагрузке

;

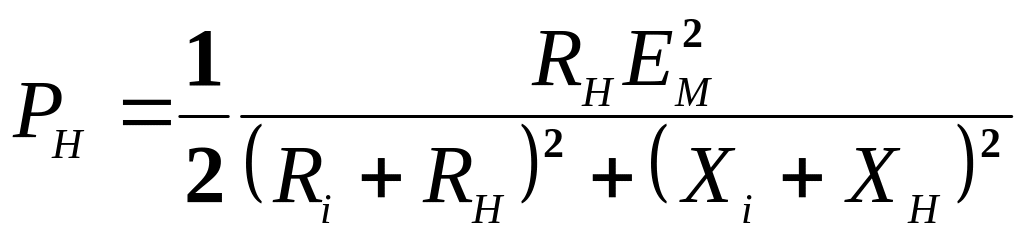Найдем условия, когда .

Во первых, потребуем Хн = -Хi.

Во вторых найдем максимум по второй переменной ( по Rн). Для этого надо взять производную по Rн от функции

;

и ее приравнять нуля. В результате получим Rн = Ri

Итак, условие согласования по максимальной мощности на нагрузке

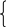; или

;;

В режиме согласования по мощности в нагрузке выделяется мощность равная . Это составляет 50% от мощности развиваемой источником сигнала, т.е. Напряжение на нагрузке , следовательно, к.п.д. в режиме согласования по мощности составляет 50% , т.е. .

7.6. Согласование четырёхполюсников

Часто четырёхполюсники являются передающим (согласующим) звеном между источником сигнала и нагрузкой. Определим условие, когда четырёхполюсник оказывается согласованным, т.е. условие, при котором через четырёхполюсник от источника сигнала в нагрузку передаётся наибольшая мощность.

Рассмотрим условие согласования на примере пассивного симметричного четырёхполюсника ( ). Его входное сопротивление зависит от сопротивления нагрузки

,

а потому его можно выбрать таким, чтобы

следовательно , где - характеристическое или волновое сопротивление. Волновое сопротивление это специфический параметр четырехполюсника.

Четырехполюсник считают согласованным, если внутреннее сопротивление источника Ri и сопротивление нагрузки Rн равны волновому сопротивлению Zв, т.е. Ri =Rн = Zв.

7.7. Соединение четырехполюсников

При анализе электрических цепей часто возникает задача определения параметров сложных четырёхполюсников, образованных путём соединения нескольких простых параметры которых известны.

Четырёхполюсники могут быть соединены следующим образом:

1. Каскадное.

2. Последовательное.

При последовательном соединении четырёхполюсники удобно описывать Z-параметрами, причём новый четырёхполюсник будет иметь Z-параметры равные сумме Z-параметров отдельных четырёхполюсников .

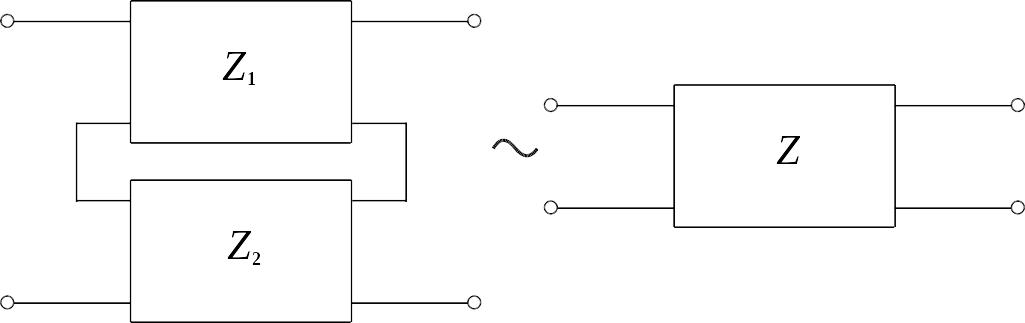
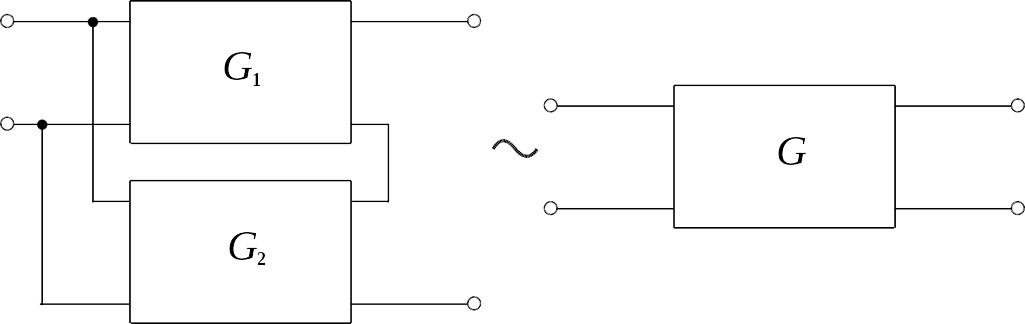
3. Параллельное.

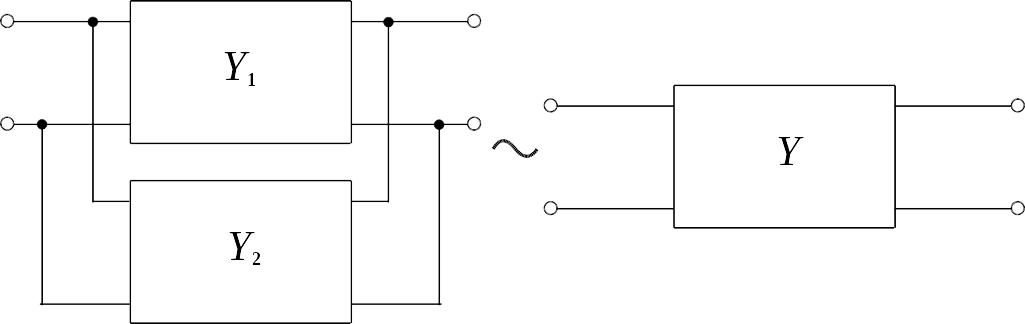
4. Последовательно - параллельное.

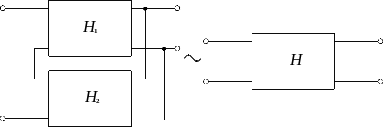
5. Параллельно – последовательное.