ЗАДАЧА 1

Для балки, показанной на рис. 1.1, построить эпюру изгибающих моментов и поперечных сил, подобрать поперечное сечение - двутавр, если [ ] = 160 МПа.

Дано М = ql², F = 1,5ql, q =25кН/м, l=0,6м.

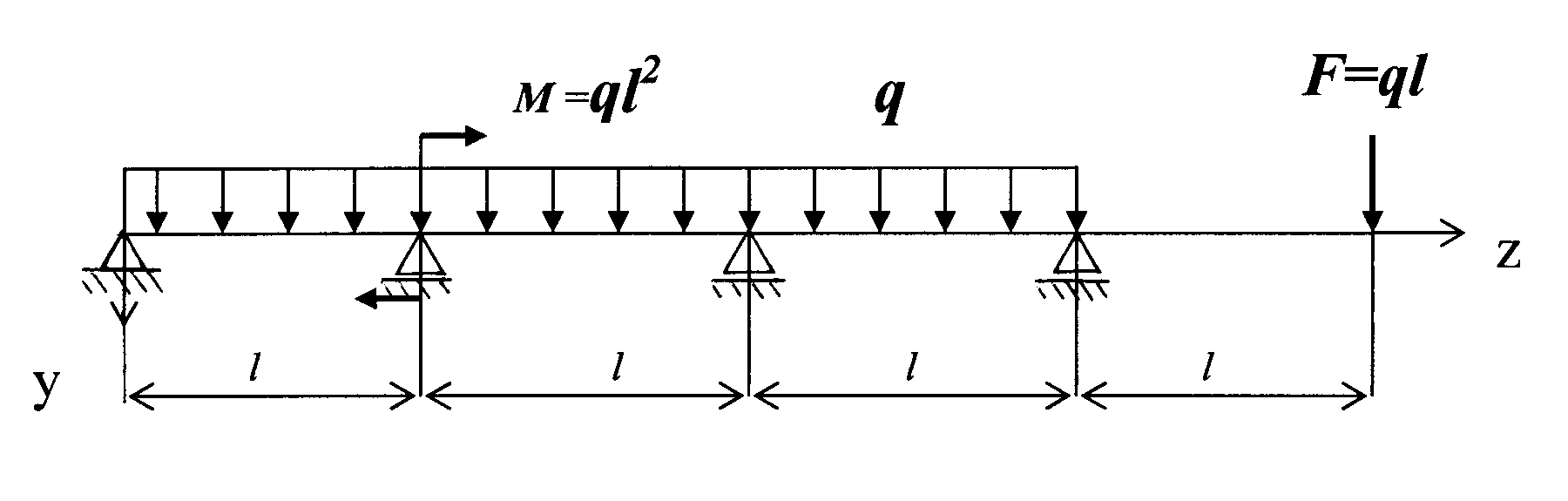
Рис. 1.1

Решение

Определяем степень статической неопределимости балки. Показываем реакции опор. В начале балки опора шарнирно неподвижная. В ней возникают две реакции – вертикальная и горизонтальная. Остальные опоры шарнирно подвижные. Так как горизонтальных сил на балку не действует, то, следовательно, горизонтальной реакции не возникает. Таким образом, на опорах возникают только четыре вертикальных реакций. Для определения этих реакций можно использовать только два уравнения статики (суммы моментов). Тогда степень статической неопределимости

S = 4 – 2 = 2.

Поэтому задача два раза статически неопределимая.

Решаем задачу методом сил. На рис. 1.2 показаны З.С.- заданная система. О.С. –основная система, полученная из заданной врезанием шарниров на опорах.

«Лишними неизвестными» будут моменты на опорах Х₁ иХ₂.

Эквивалентная система Э.С. – отдельные балки АВ, ВС и СДЕ загруженные заданными нагрузками и лишними неизвестными, действующими на опорах В и С.

Для определения неизвестных Х₁ и Х₂ записываем систему двух канонических уравнений метода сил.

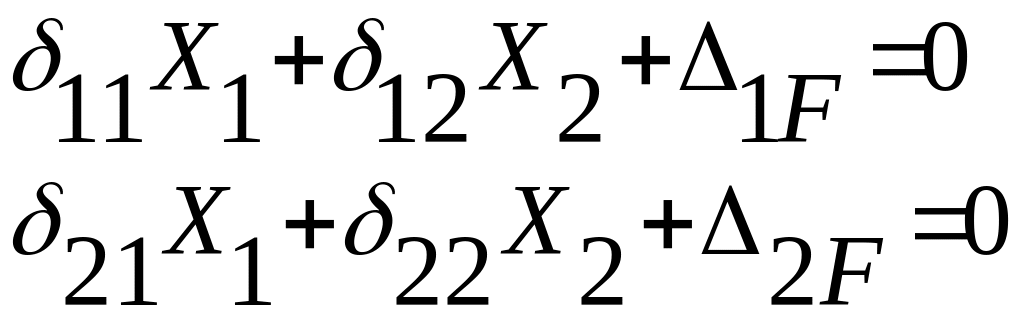
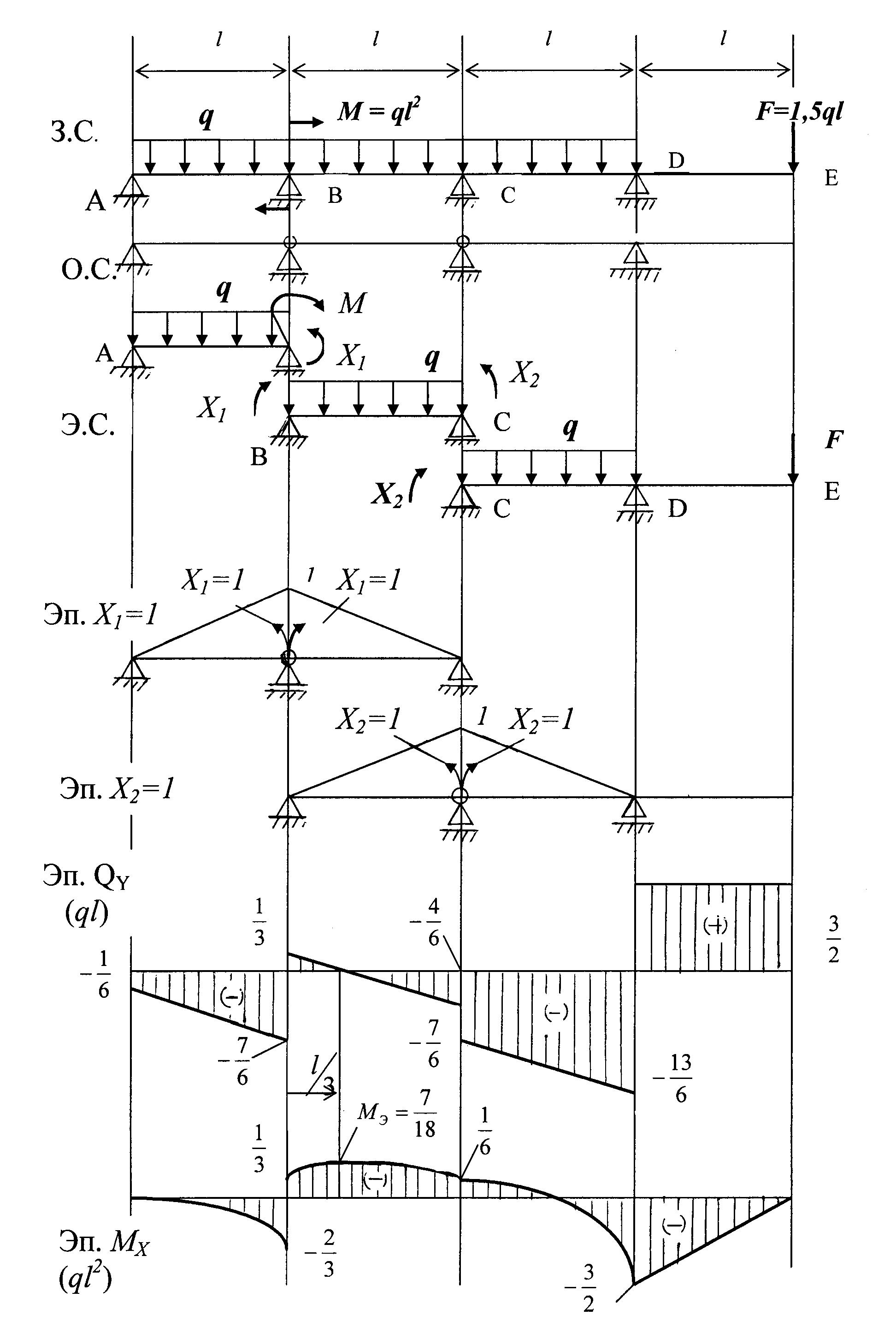
Рис. 1.2

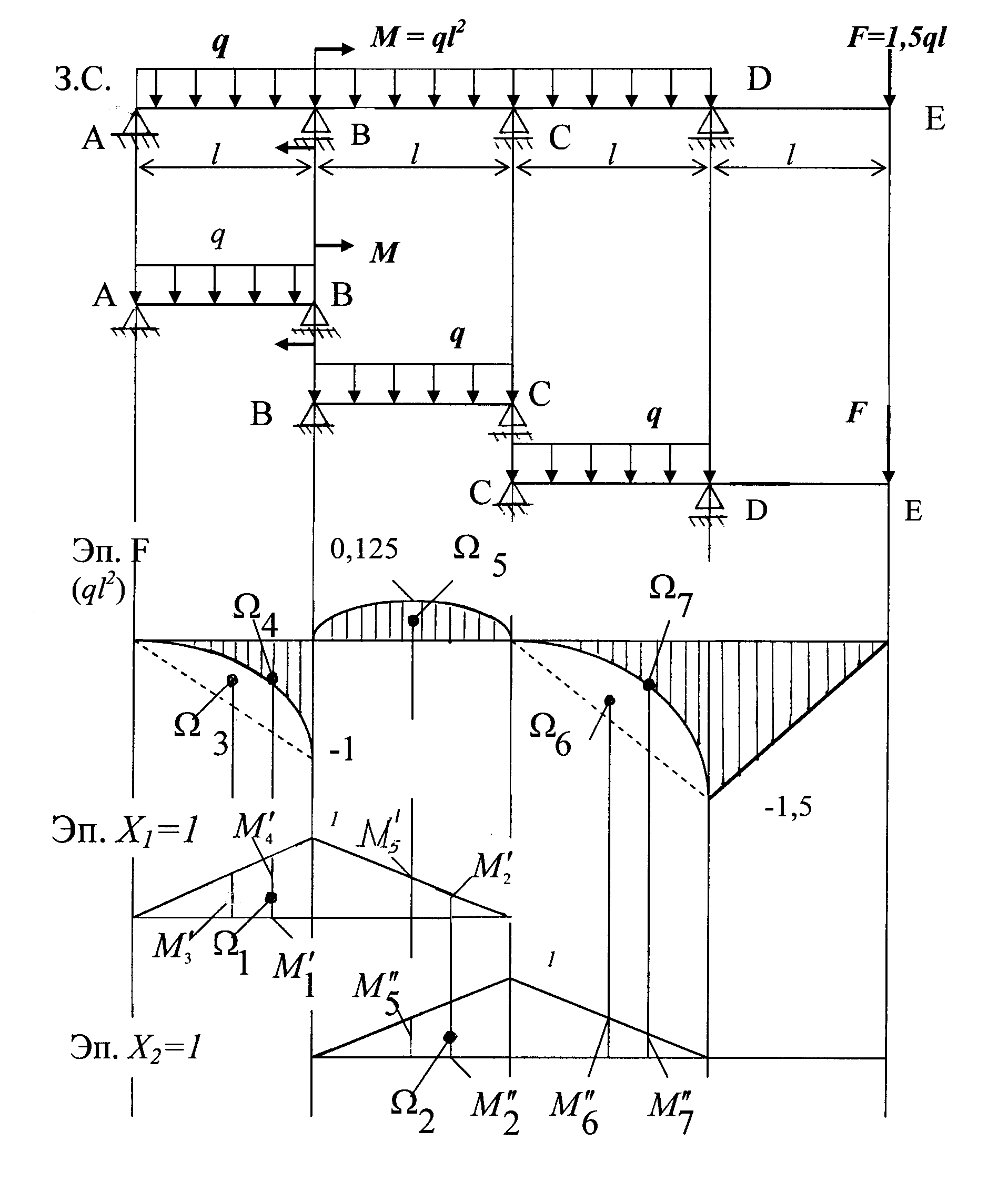
Рис. 1.3

Для определения коэффициентов этих уравнений строим эпюры изгибающих моментов от Х₁ =1, Х₂ = 1 и внешних нагрузок Эп. F (рис. 1.3 ).

Перемножаем эпюру Х₁ = 1 самое на себя. Показываем центр тяжести и момент и используя способ Верещагина, получим:

l;

Перемножаем эпюры Х₁ = 1 и Х₂ = 1, аналогично, имеем:

;

Перемножаем эпюру Х₂ = 1 самое на себя, вычисляем :

;

Перемножаем эпюры от внешних нагрузок (эп.F) на эпюру Х₁=1;

;

Перемножаем эпюры (эп. F) и Х₂=1. Напомним, что по способу Верещагина эпюра изгибающих моментов разбивается на простейшие фигуры (треугольник, прямоугольник и т.д.), показывают их центры тяжести , на единичной эпюре над ними показывают моменты и вычисляют:

.

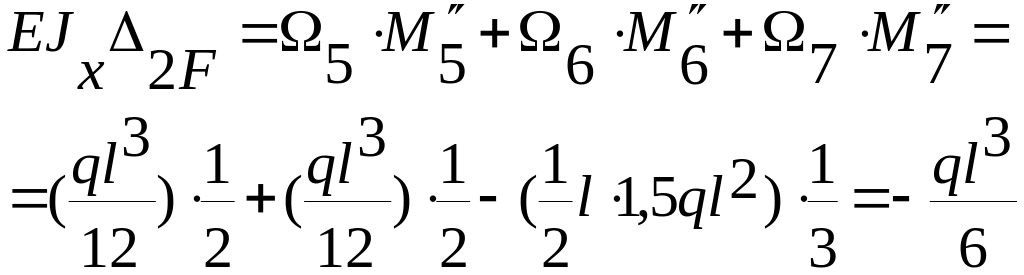Знак минус ставится, когда перемножаемые эпюры разноименные. Подставляем подсчитанные коэффициенты в канонические уравнения:

Решая эту систему, находим:

; .

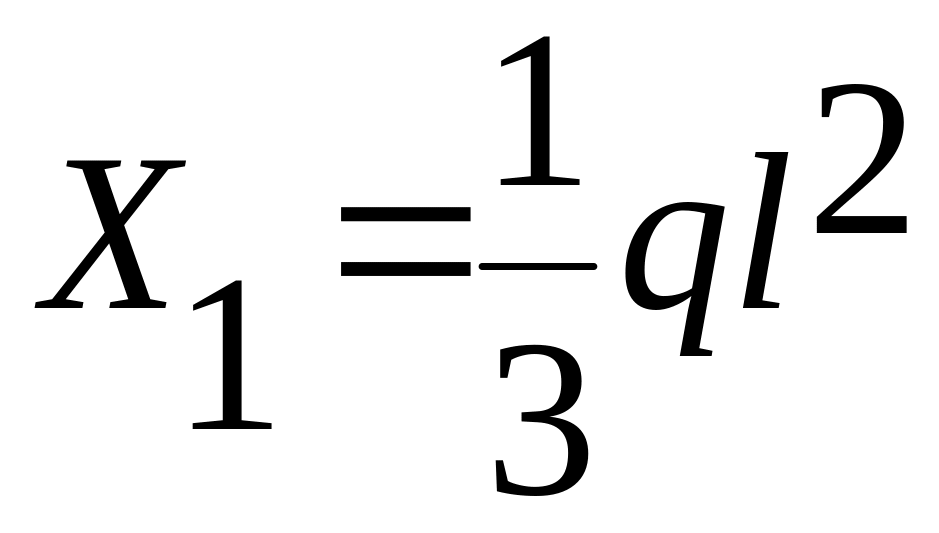Далее к каждой балке АВ, ВС и СДЕ прикладываем заданные нагрузки и подсчитанные значения лишних неизвестных Х₁ и Х₂, строим эпюры изгибающих моментов М_Х и поперечных сил Q_Y.

Строим эпюры на каждом участке балки.

Участок АВ (рис. 1.4 ) ( 0 ≤ z ≤ l ):

Находим реакции опор .

∑mom A = 0; ;

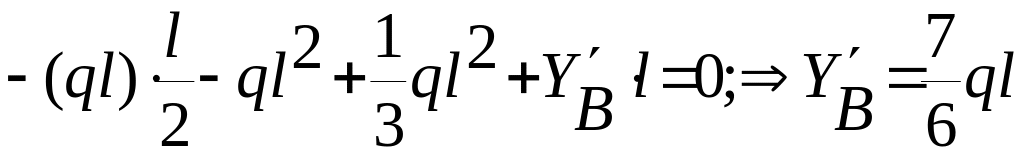∑mom B = 0; => ;

Проверка реакций.

∑пр. у =0; = 0.

Строим эпюры .

Q_Y = -Y_A – qz₁;

Т.А z = 0, Q_Y = -Y_A = - ; т. В z = l,

;

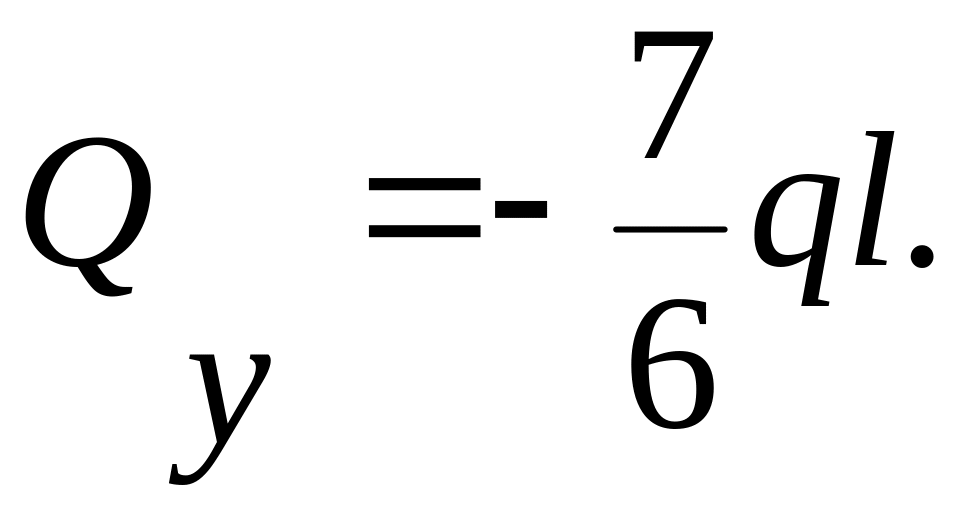
т. А z = 0, М_Х =0; т. В z = l, M_X = - .

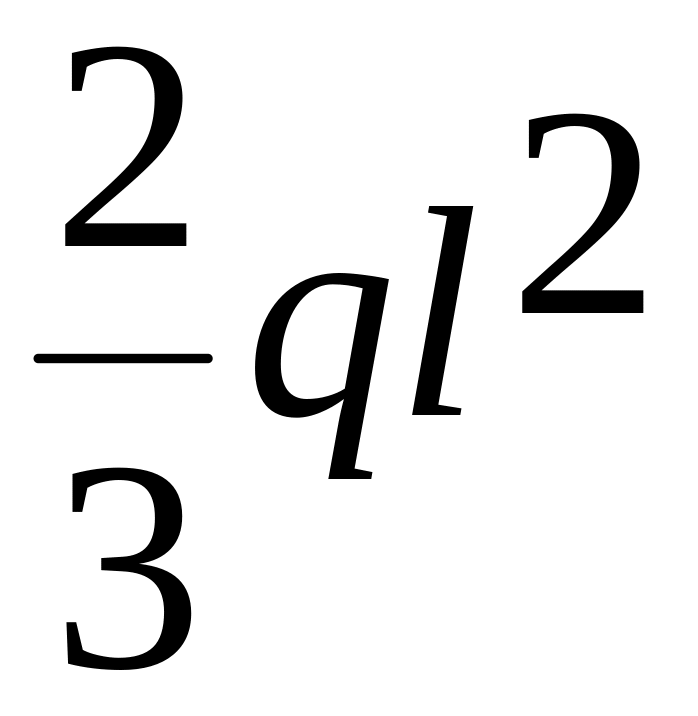находим значение М_Х при z = 0,5 l, М_Х = - .

Участок ВС (рис. 1.5 ) ( 0 ≤ z ≤ l ):

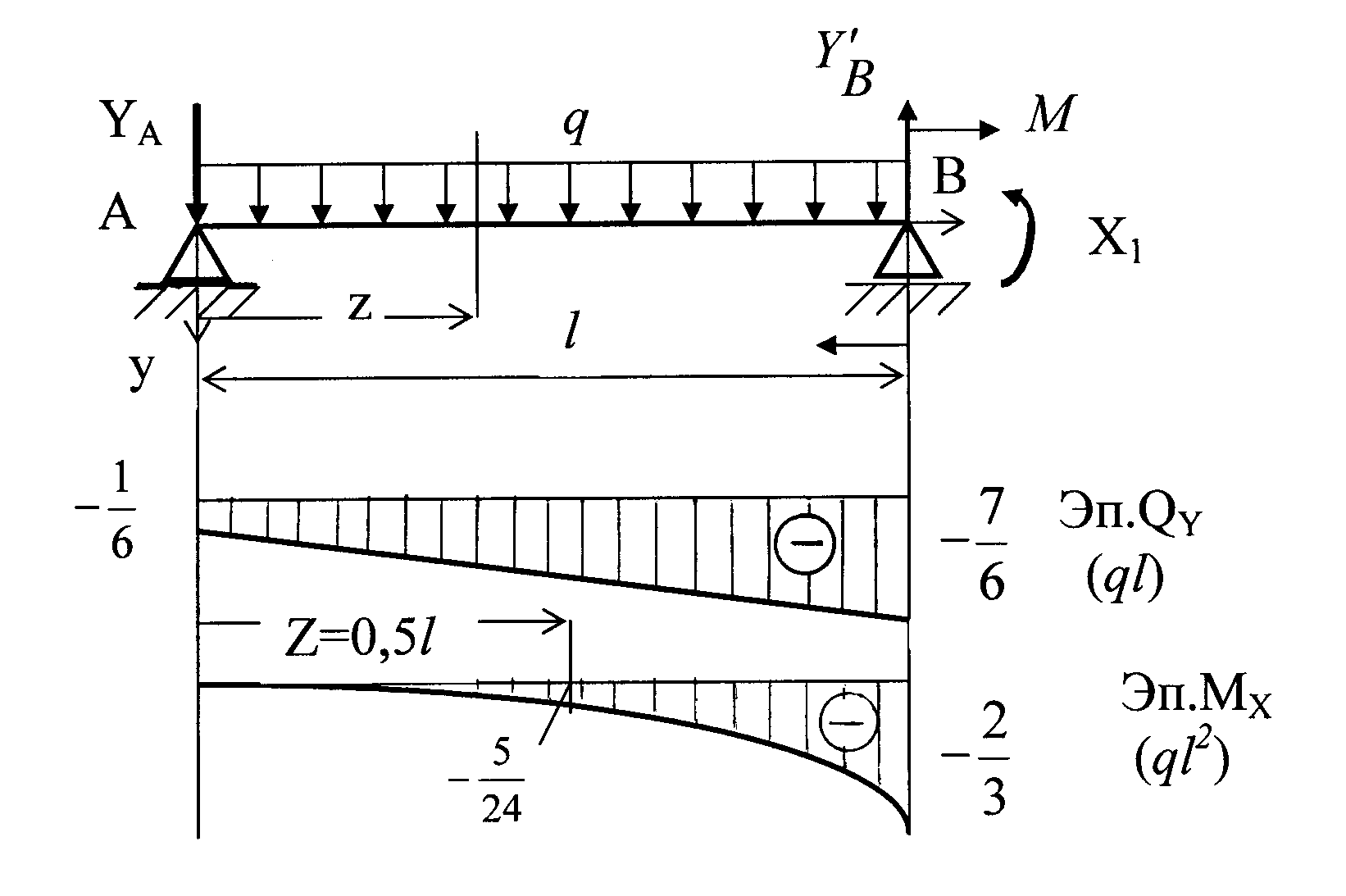
Рис. 1.4

Находим реакции опор.

∑mom B =0; (- ; => ;

∑mom C =0; ; => ;

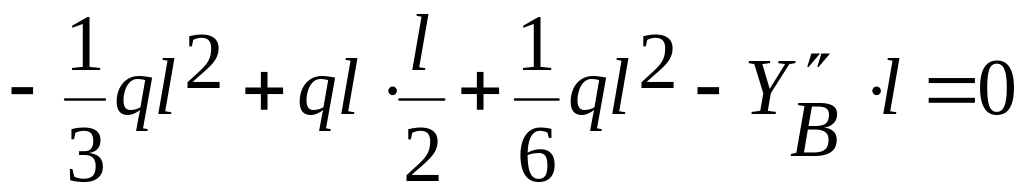Проверка реакций.

∑пр.у = 0; .

Строим эпюры Q_Y и M_Х .

.

;

Т. В z = 0, ; т.С z = l,

;

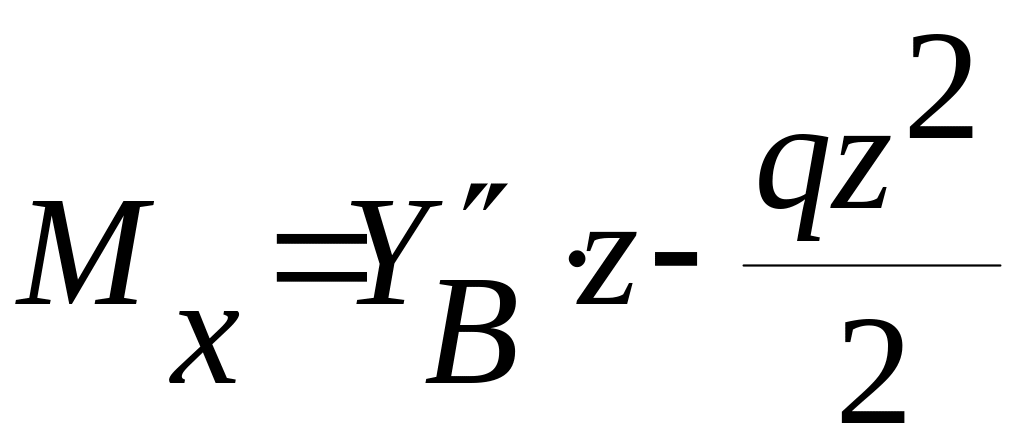Т. В z = 0, ; т. С z = 0, .

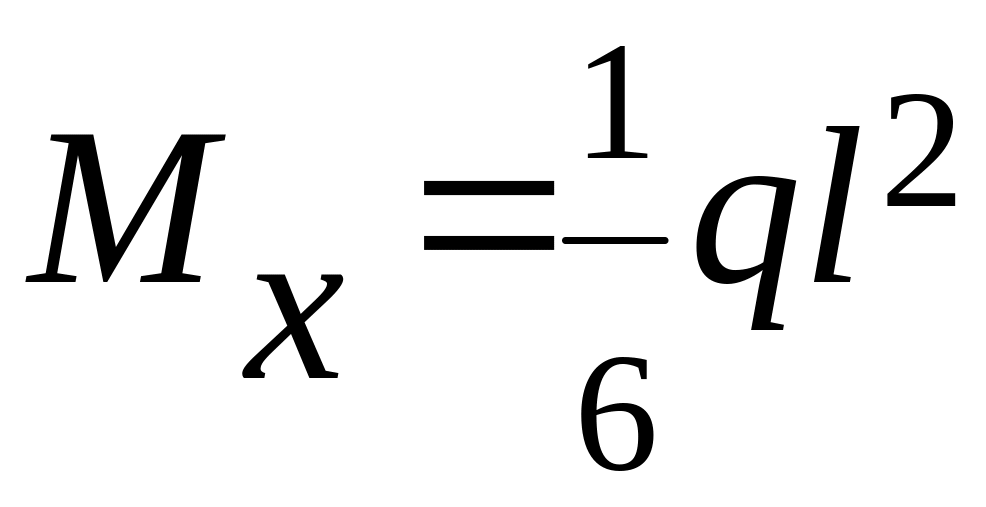Точка перегиба.

=> ;

Рис. 1.5

.

Балка СДЕ (рис. 1.6)

Находим реакции опор.

С = 0; ; => ;

D =0; => ;

Проверка реакций.

= 0;

Строим эпюры изгибающих моментов и поперечных сил.

Участок CD ( 0 ≤ z₁ ≤ l ):

Т.С ; т. D z₁ =l; .

;

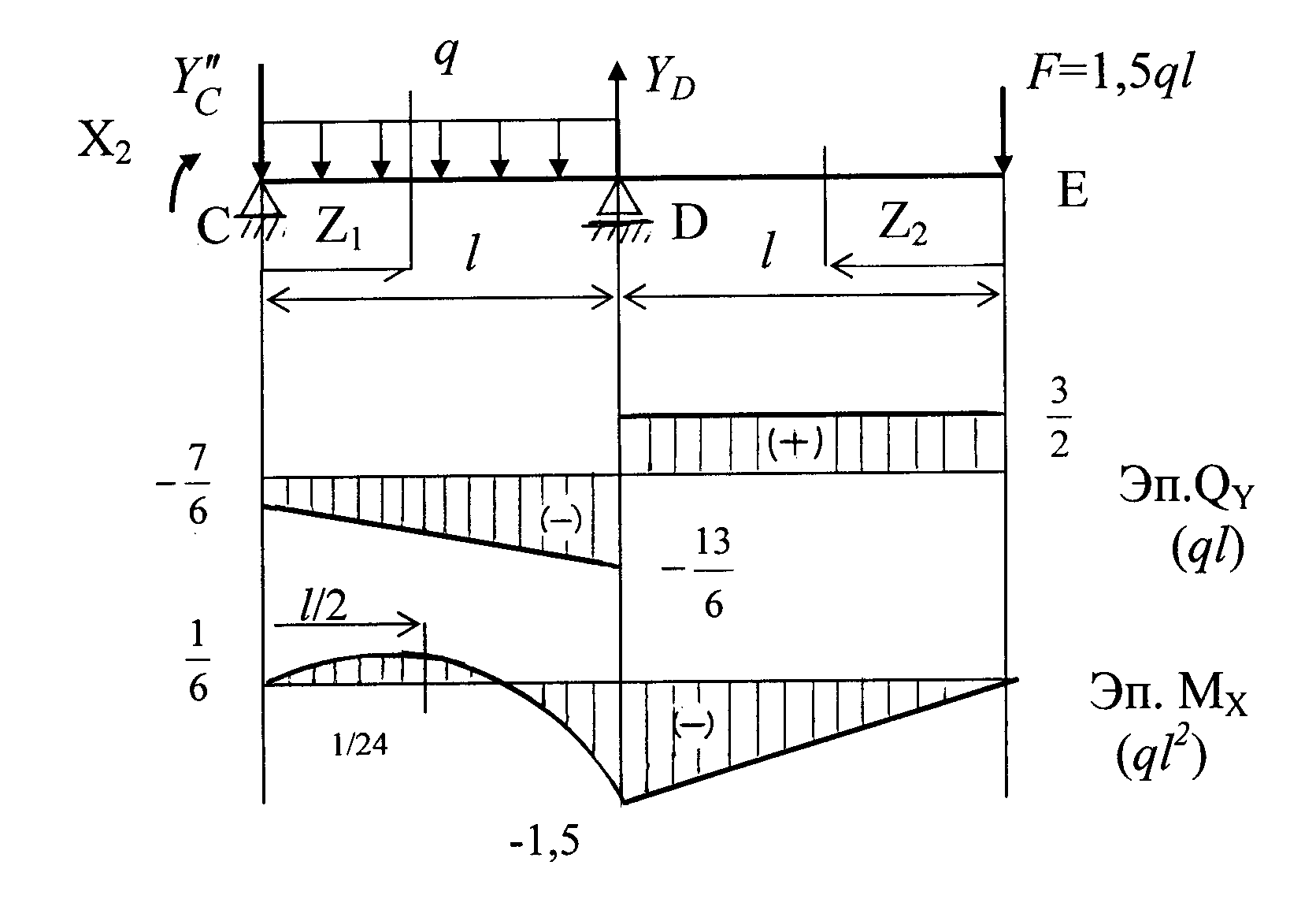
Рис. 1.6

Т.С z₁=0, ; т. D z₁ = l, .

Значение M_X при z₁=0,5l: .

Участок ED ( 0 ≤ z₂ ≤ l ):

Q_Y = F = 1,5ql;

M_X = -1,5ql·z²;

Т. Е z₂ = 0, M_X = 0; т. D z₂ = l, M_X = -1,5ql.

Результирующие эпюры изгибающих моментов и поперечных

сил в балке от заданных нагрузок приведены на рис. 1.2.

Проверка правильности решения.

Перемножаем эпюры М_Х и Х₁=1 ( рис. 1.7).

Рис. 1.7

EJ_XП₁ = =

= = 0.

Рис. 1.8

Перемножаем эпюры М_Х и Х₂=1 (рис.1.8).

EJ_XП₂ = =

= +

+( = 0.

Подбираем размер поперечного сечения балки.

Из эпюры изгибающих моментов М_Х находим:

1,5·25·10³ ·0,62=13500(Нм);

Необходимый момент сопротивления сечения балки равен:

м³

Подбираем сечение двутавра ГОСТ 8239-89 № 16 W_X=109см³.

ЗАДАЧА 2

Для, показанной на рис. 2.1 раме построить эпюры изгибающих моментов и поперечных сил, а также подобрать размеры прямоугольного сечения h=2b.

Дано F = 1,5ql, q =25кН/м, l=0,6м.

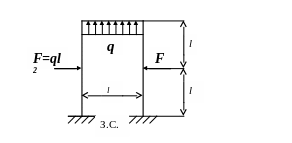
Рис. 2.1

Решение

Рама имеет две опоры – жесткие заделки. В каждой из них возникает опорный момент, горизонтальная и вертикальная реакции. Таким образом, получается шесть реакций. Вычитая три уравнения статики, получаем, что рама должна иметь степень статической неопределимости – три.

Однако рама, вместе с приложенными нагрузками, обладает симметрией относительно вертикальной оси. В этом случае если разрезать раму при выборе основной системы по оси симметрии, то вместе разреза будут возникать только две «лишние» неизвестные Х₁ и Х₂, кососимметричные неизвестные Х₃ равны нулю. Таким образом получаем, что данная рама с приложенными к ней нагрузками два раза статически неопределима. На рис. 2.2 показана основная система (О.С.) – рама разрезана по оси симметрии и эквивалентная система (Э.С.), когда к основной системе приложены лишние неизвестные Х₁,Х₂ и заданные нагрузки - сосредоточенная сила F и распределенная q

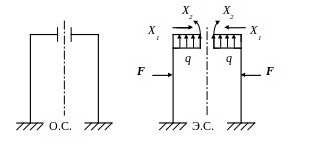
Рис. 2.2

Записываем систему канонических уравнений метода сил:

Для определения коэффициентов канонических уравнений строим эпюры изгибающих моментов от Х₁ =1, Х₂ =1 и заданных нагрузок, которые показаны на рис. 2.3.

Эп. F

(ql²)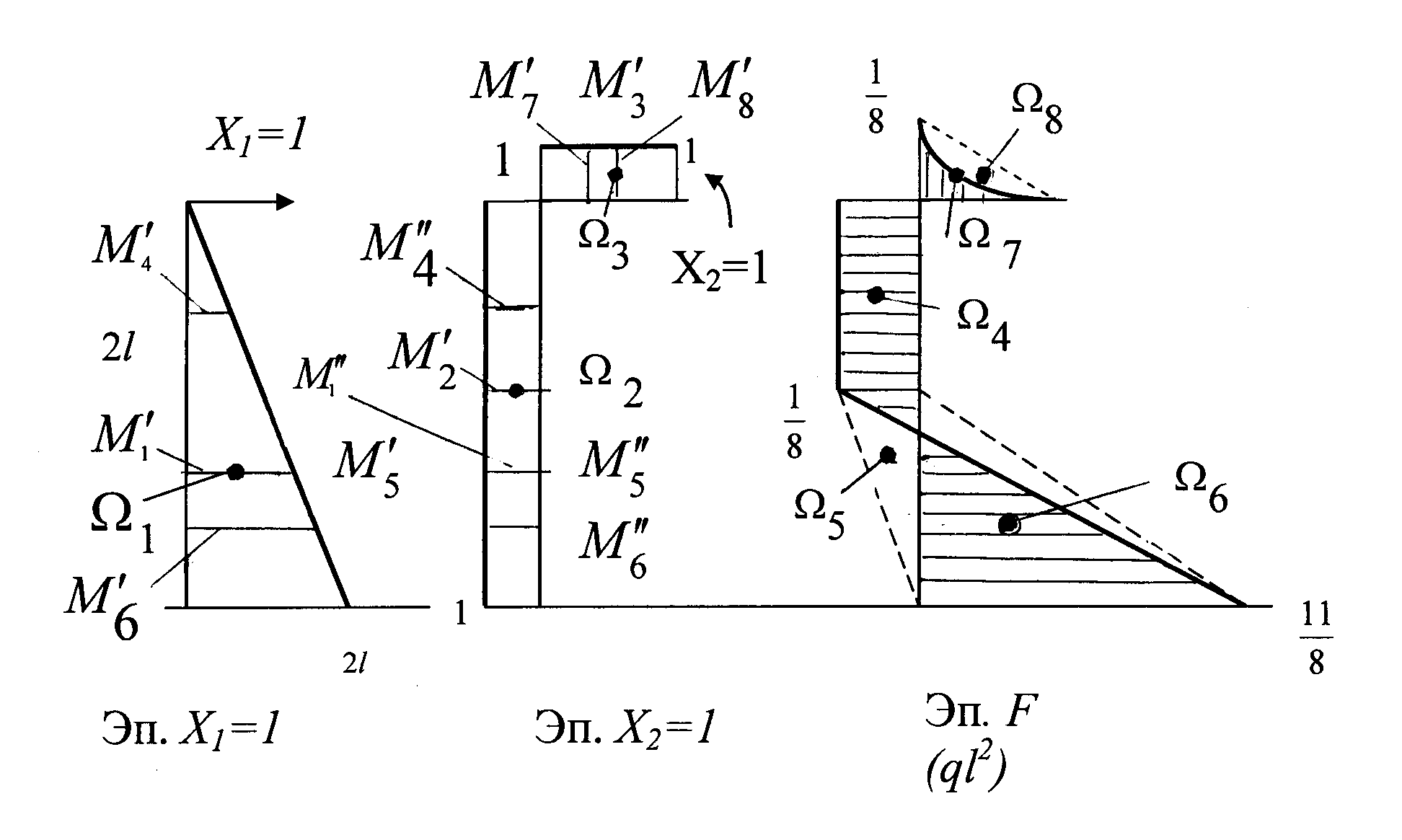

Рис. 2.3

Перемножаем эпюру Х₁ = 1 самое на себя:

;

Перемножаем эпюру Х₁ = 1 на эпюру Х₂ = 1:

;

Перемножаем эпюру Х₂ = 1 самое на себя:

;

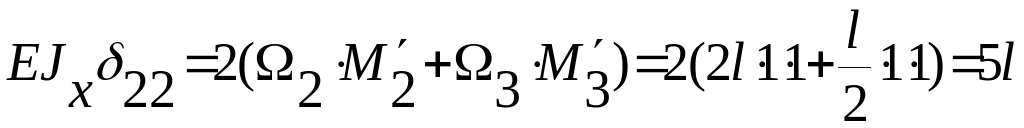Перемножаем эпюру Х₁ =1 на эпюру F:

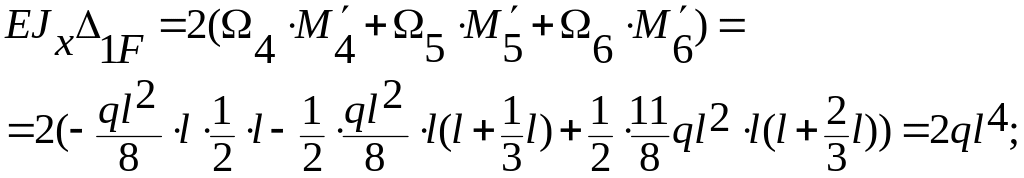
Перемножаем эпюру Х₂ = 1 на эпюру F:

=

=2( .

Подставляем полученные значения коэффициентов в канонические уравнения, решаем систему и находим значения «лишних» неизвестных Х₁ и Х₂.

; .

Прикладываем Х₁ и Х₂ с учетом знаков к эквивалентной системе и строим эпюры изгибающих моментов и поперечных сил (рис.2.4).

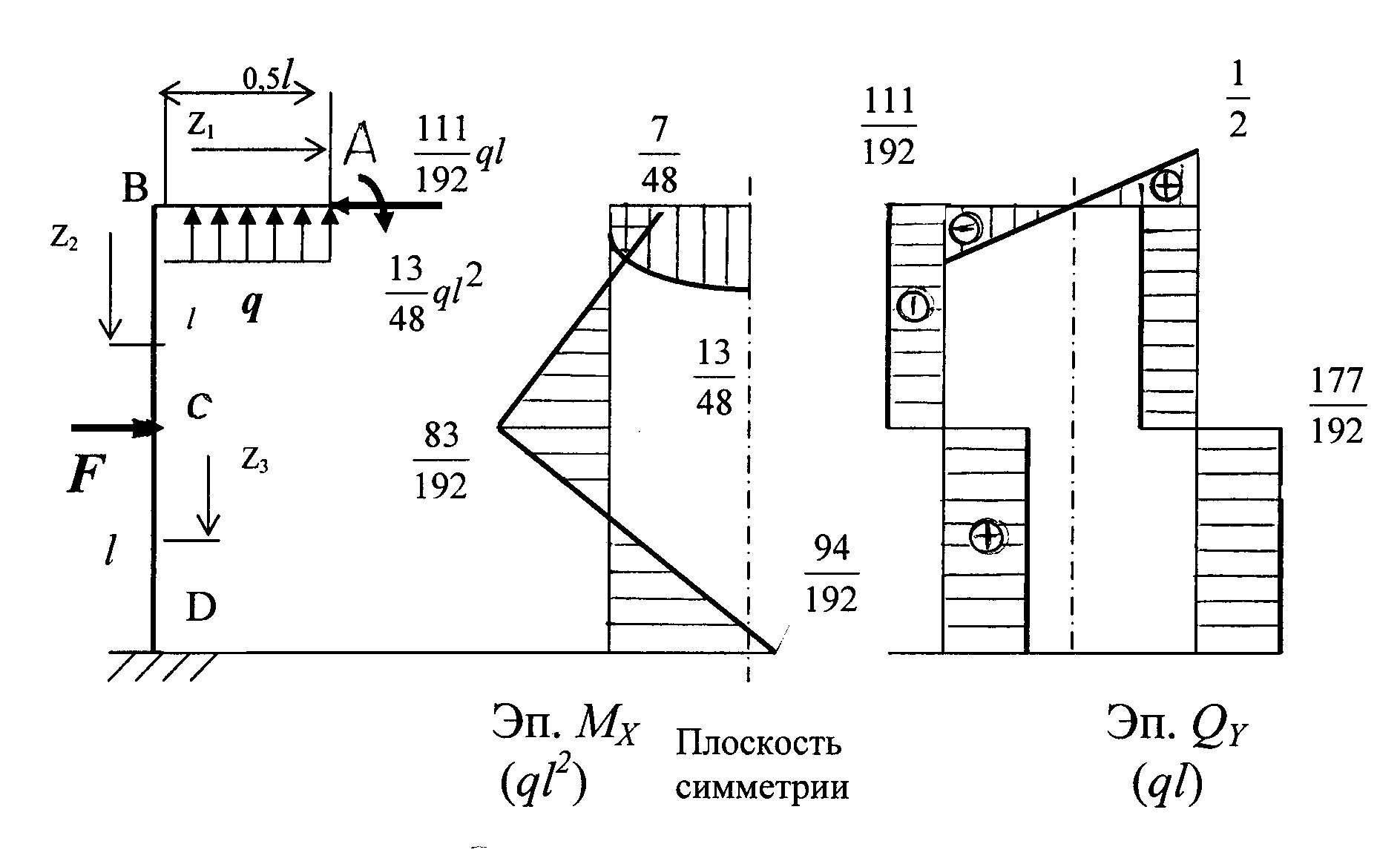
Рис. 2.4

Участок АВ ( 0 ≤ z₁ ≤ ):

;

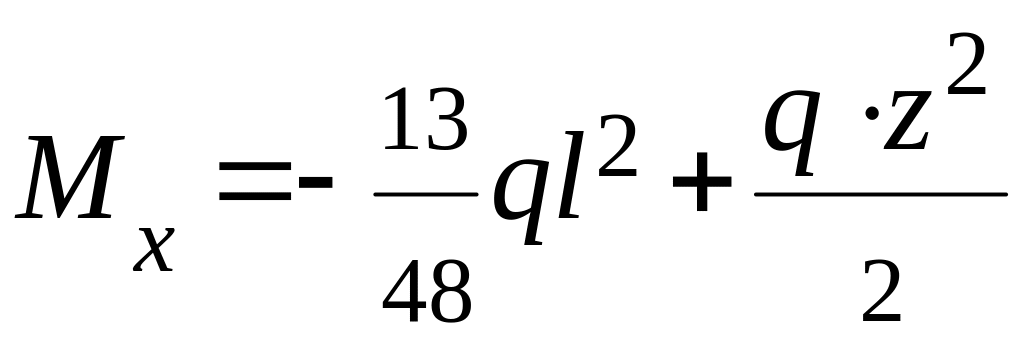Т. A ; т. В ; .

Q_y = -q·z₁;

Т.А z₁ = 0; Q_y = 0; т. В z₁ = l/2; Q_y = .

Участок ВС ( 0 ≤ z₂ ≤ l ):

;

Т. В z₂ = 0; ;

Т. С z2 = l; .

Участок СД ( l ≤ z₃ ≤ 2l ):

Т.С z₃ = l; ;

Т. D z₃ = 2l; .

Выполним проверку правильности решения задачи.

Перемножим полученную эпюру изгибающих моментов на эпюры от Х₁ =1 и Х₂=1.

Рис. 2.5

=

=

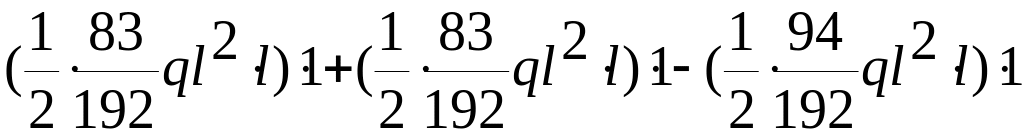+ = 0.

Задача решена верно.

Определим размеры прямоугольного сечения рамы.

.

Приравнивая =100МПа; = ql²; q =25кН/м; l=0,6м, и зная W_X =(b·h²)/12 и h =2b,

получим: . b=4·10^-2 м, h = 8·10^-2м.

ЗАДАЧА 3

Ломаный брус (рис. 3.1) загружен силами = 2кН, = 1кН, равномерно распределенной нагрузкой интенсивностью q = 1 кН/м и моментом Т =1 кНм. Размеры бруса a = 1 м, с = 1 м.

Требуется подобрать:

на участке АВ – размер диаметра круглого сплошного сечения;

на участке ВС - размеры h и b ( h = 2 b ) прямоугольного сечения. Материал бруса - сталь , = 160 МПа, G = МПа.

При расчетах использовать теорию прочности максимальных касательных напряжений.

Построение эпюр изгибающих и крутящего моментов. В сечениях бруса под действием приложенных внешних сил и моментов возникают изгибающие и крутящий моменты, поперечные и нормальная силы. При расчете на прочность таких брусьев влиянием поперечных и нормальных сил обычно пренебрегают. Поэтому для рассматриваемого примера эпюры поперечных и нормальных сил не строим.

Приступая к решению задачи, прежде всего, необходимо на каждом участке бруса (см. рис.3.1,а) показать скользящую систему координат xyz в сечениях А и В (ось z должна быть направлена вдоль оси бруса).

Далее, делая обход со свободного конца бруса по его контуру (переходя от одного участка к следующему участку бруса, наблюдатель не должен пересекать ось z ), записываем выражения изгибающих и крутящих моментов для текущих сечений каждого участка бруса.

Участок АМ: (плоскость zy) = 0; (плоскость zx) = q ; = Т. Участок МВ:

= =q(0.4a)( -0.2a); = Т.

Участок ВЕ:

= (0,6a); = T + q( 0,4 a) ; = - q(0,4a)(0,8a).

Участок ЕС:

= (0,6a); = T+q (0,4a)

= - q(0,4a)(0,8a).

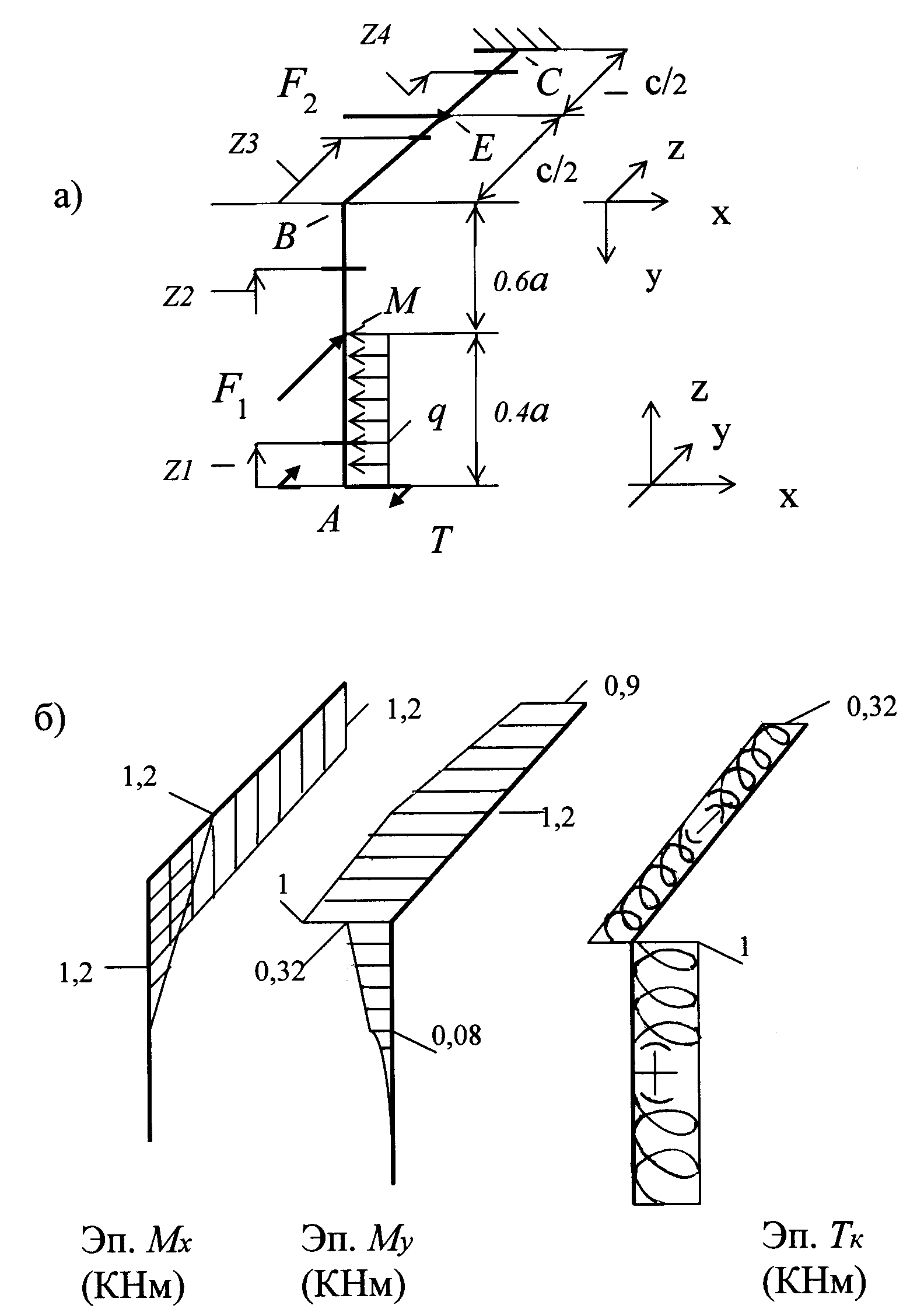
Рис.3.1

По полученным уравнениям, задаваясь значениями координаты z, подсчитываем величины ординат , , в начале и конце каждого участка и строим соответствующие эпюры (рис.3.1,б). Напоминаем, что эпюры изгибающих моментов строим со стороны сжатых волокон бруса, а эпюры крутящих моментов можно строить в любой плоскости, но обязательно следует указывать знаки.

Выявление наиболее нагруженных сечений участков бруса.

На каждом участке опасное сечение или несколько таких сечений, если есть сомнение, устанавливают путем анализа эпюр изгибающих и крутящих моментов. В рассматриваемом примере из построенных эпюр (см. рис.3.1,б) следует, что на участке бруса АВ таким сечением является сечение В, а на участке ВС - сечение Е. Для проведения дальнейших расчетов рекомендуем опасные сечения изображать отдельно и в них показывать действующие изгибающие и крутящий моменты, а также соответствующие им эпюры нормальных и касательных напряжений.

Расчет диаметра круглого поперечного сечения бруса – на участке АВ.

На рис.3.2,а изображено опасное сечение В. Показаны изгибающие моменты = 1,2 кНм, = 0,32 кНм и крутящий момент = 1 кНм.

Для бруса круглого или кольцевого поперечного сечения любая диаметральная ось является главной, поэтому при действии двух изгибающих моментов он не испытывает косого изгиба. Моменты могут быть приведены к суммарному

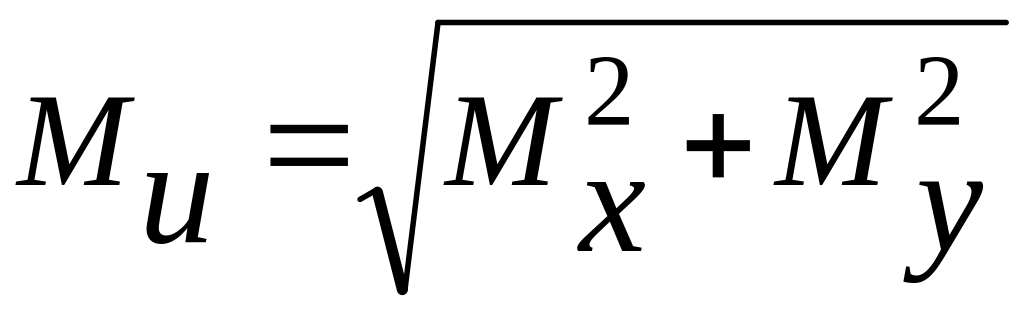
Из эпюр нормальных и касательных напряжений (рис.3.2,б) следует, что наиболее опасными точками в рассматриваемом сечении будут точки 1 и 2. Материал бруса испытывает напряженное состояние растяжения - сжатия и сдвига, т.е. находится в условиях сложного напряженного состояния. Оценку прочности в этом случае необходимо проводить с применением одной из теорий прочности.

Эквивалентное напряжение для такого случая двухосного напряженного состояния по теории максимальных касательных напряжений подсчитывается :

_{= .}

Зная, что для круглого сечения полярный момент сопротивления ( - момент сопротивления сечения при изгибе), эту формулу, можно записать в виде:

, (3.1)

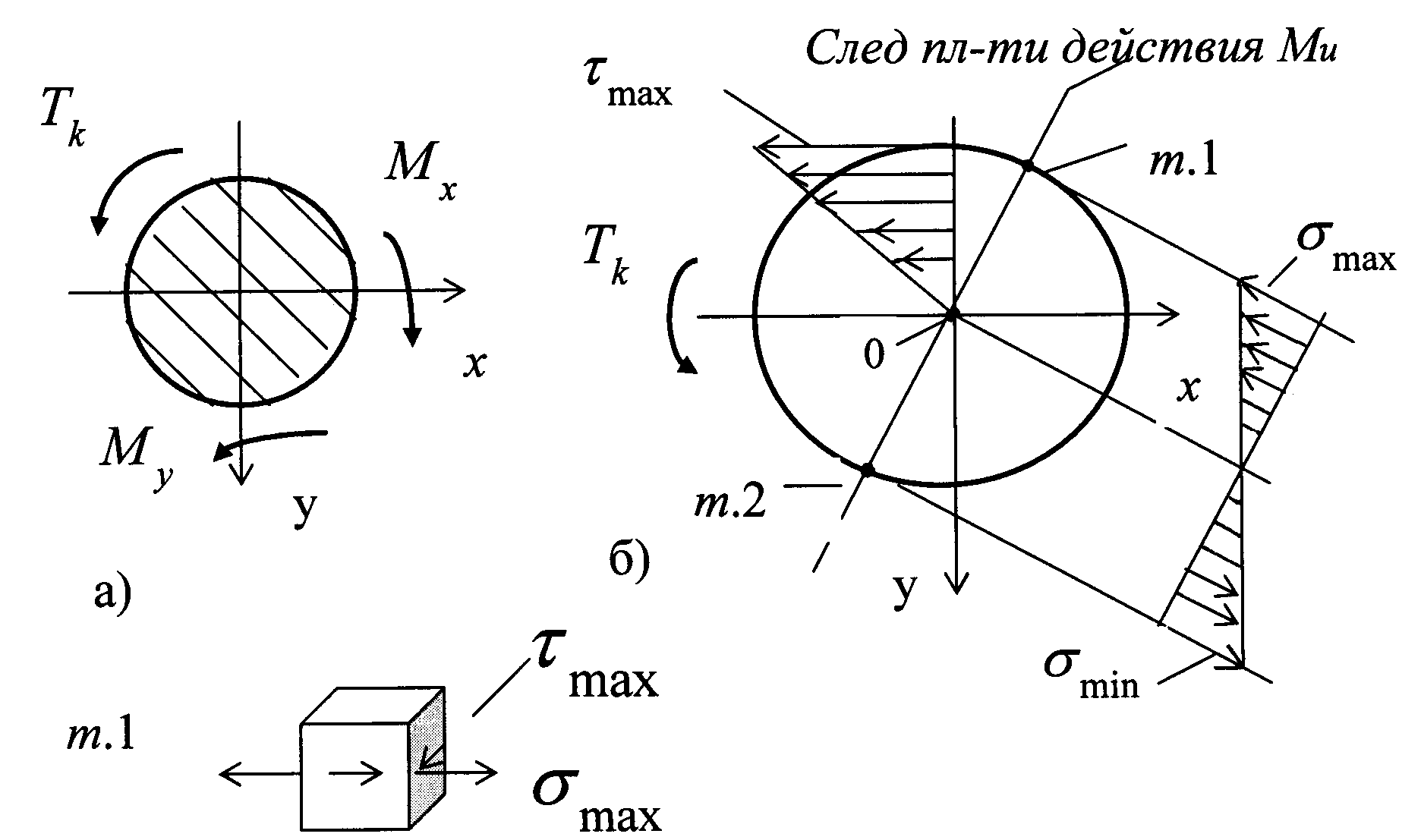
Рис.3.2

где и - крутящий и изгибающий моменты.

Подбор безопасных размеров сечения (проектный расчет) проводится следующим образом. Для опасной точки вычисляют значение эквивалентного напряжения, в которое входит и неизвестная величина момента сопротивления сечения , выраженная через размеры сечения. Приравнивая эквивалентное напряжение допускаемому

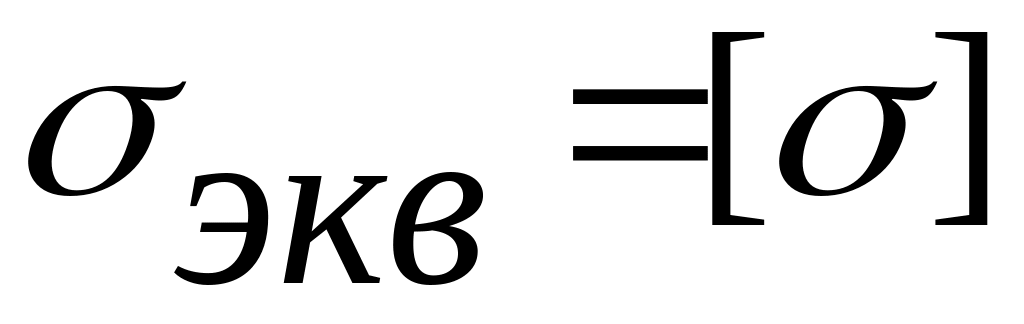(3.2)

вычисляют величину , а следовательно, и безопасные размеры сечения.

Вернемся к рассматриваемому примеру. Из условия задачи следует, что материал бруса пластичный материал – сталь, одинаково сопротивляющаяся растяжению – сжатию. По теории прочности максимальных касательных напряжений эквивалентное напряжение для самой опасной точки 1 сечения определяется по формуле (3.1):

где было принято .

Учитывая (3.2), определим безопасную величину диаметра круглого сечения

Округляя найденное значение в миллиметрах до ближайшего числа из стандартного ряда (см. приложение) принимаем D = 48 мм.

Расчет размеров прямоугольного поперечного сечения бруса – на участке ВС.

Рассматривая участок ВС бруса прямоугольного сечения, необходимо показать изгибающие и крутящий моменты, действующие в опасном сечении Е, а также соответствующие им эпюры напряжений (рис.3.3).

= 1,2 кНм ; = 1,2 кНм; = 0,32 кНм.

Опасными точками могут быть точки 1, 2. 3, т.к. согласно эпюрам, в этих точках напряжения достигают своих экстремальных значений.

В точке 1 складываются нормальные напряжения от двух изгибающих моментов , и возникает одноосное напряженное состояние:

,

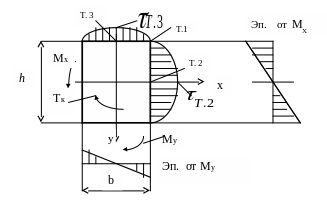
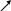точка 1 точка 2 точка 3

Рис.3.3

где , - моменты сопротивления сечения на изгиб относительно осей х и у.

Учитывая, что h = 2 b , тогда:

.

В точке 2 возникают нормальные напряжения от момента и касательные напряжения от крутящего момента :

; .

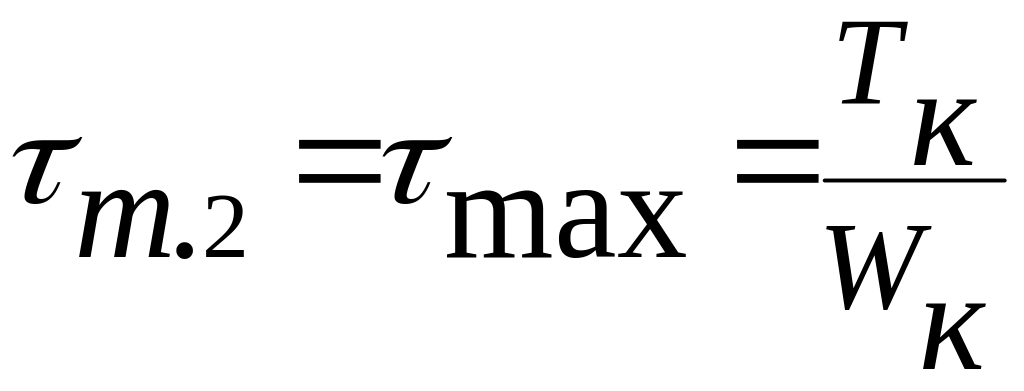Здесь - момент сопротивления сечения на кручение , где - коэффициент, определяемый по таблицам в зависимости от отношения h/b . Так, для h / b = 2, = 0.246.

Напряженное состояние в данной точке двухосное (растяжение и сдвиг). Эквивалентное напряжение по теории прочности максимальных касательных напряжений следует находить по формуле :

Аналогично вычисляем нормальные и касательные напряжения для точки 3:

; ,

где - коэффициент, определяемый так же, как и коэффициент .

Для h/b = 2 = 0.796.

Эквивалентное напряжение для этой точки:

После вычисления значений 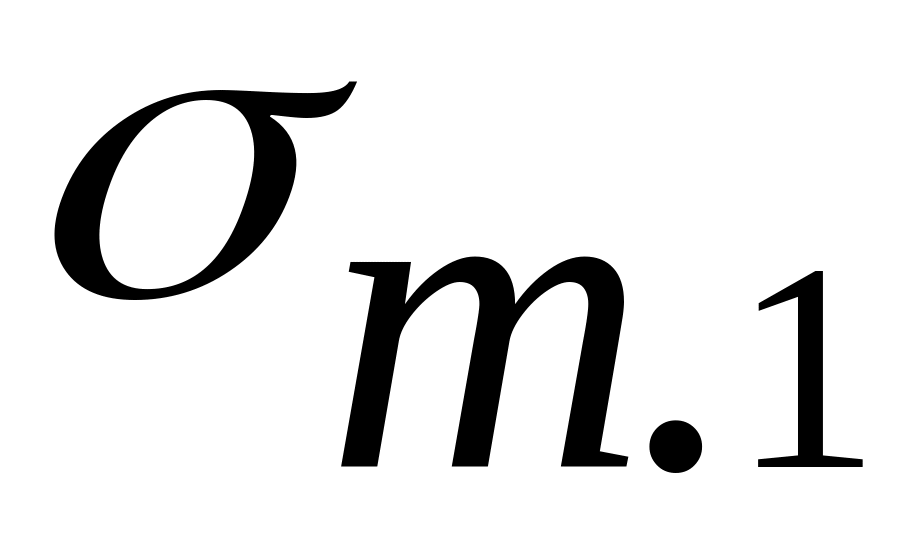, , 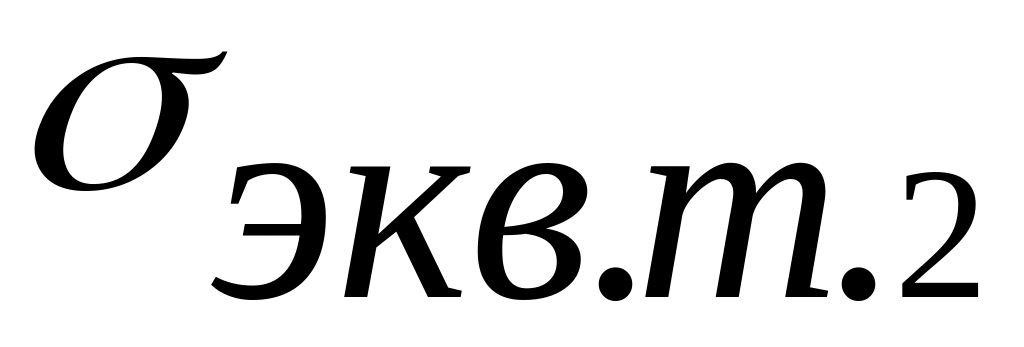следует выбрать наибольшее из них, приравнять его допускаемому напряжению = 160МПа и определить размеры сечения b и h .

В рассматриваемом примере

.

Откуда b = 32.3 мм.

Используя приложение, принимаем b =35 мм, h = 70 мм.

ЗАДАЧА 4

Тонкостенная длинная замкнутая трубка (рис.3.7,а) толщиной стенки = 2 мм и средним диаметром D = 40 мм находится под действием внутреннего давления p = 5 МПа и моментов М = 50 Нм, Т = 50 Нм. Требуется определить коэффициент запаса трубки . Материал трубки – сталь У-8 незакаленная = 250 МПа, = 430 МПа.

Определение напряжений в поперечных и продольных сечениях трубки. Решение задачи следует начинать с определения нормальных и касательных напряжений, возникающих в поперечных и продольных сечениях трубки под действием приложенных к ней внешних нагрузок. При этом следует рассматривать сечения, расположенные на достаточном удалении от концов трубки, где возникает однородное по ее продольной оси напряженное состояние. Для рассматриваемой трубки таким сечением является сечение 1-1.

Используя принцип независимости действия сил, определим напряжения в этом сечении отдельно от М , Т , а также внутреннего давления р .

От действия внешнего момента М в поперечных сечениях трубки возникает изгибающий момент = М . При этом максимальные и минимальные нормальные напряжения будут в точках С и В поперечного сечения трубки (рис.3.7,б), и их следует определять по формулам:

; .

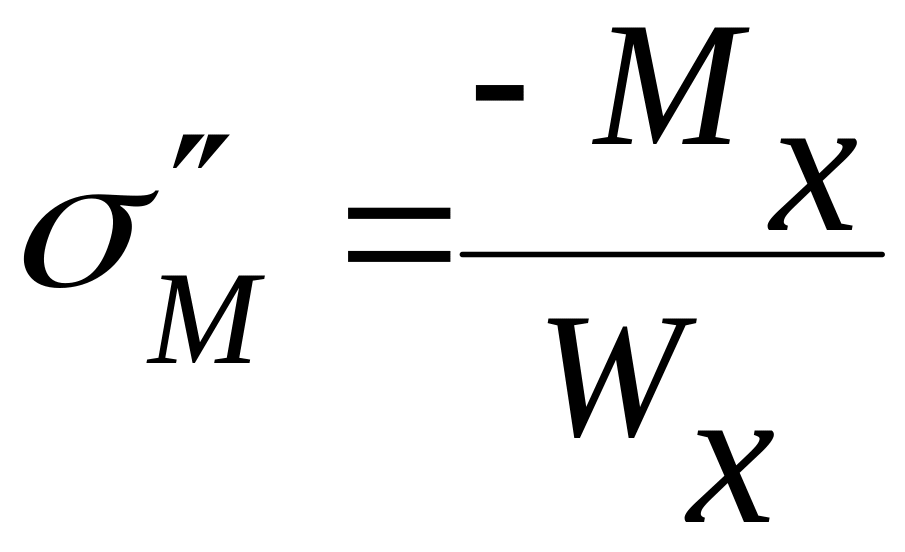где 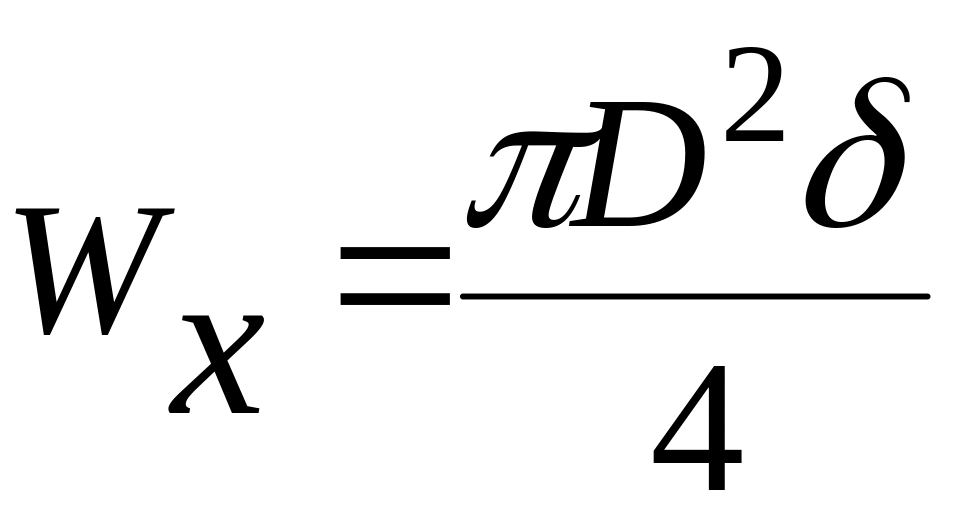- момент сопротивления поперечного сечения трубки при изгибе.

Тогда .

Рис.3.7

Внешний (скручивающий) момент Т вызывает в поперечных сечениях трубки крутящий момент = Т.

Касательные напряжения равномерно распределены по толщине стенки (рис.3.7,с), и их следует подсчитывать по формуле: ,

где - момент сопротивления сечения трубки при кручении. Величину необходимо определять как для тонкостенного кольца: .

Тогда

Под действием внутреннего давления р в продольных и поперечных сечениях трубки возникают нормальные напряжения и (рис.3.7,д).

Напряжение определим из формулы Лапласа:

+ = ,

где и - радиусы кривизны поверхности трубки по направлениям действия напряжений и .

Принимая =D/2 ; ∞, находим:

.

Напряжение установим следующим образом.

Действующее на крышку трубки давление p вызывает растяжение трубки в осевом направлении силой .

Величину напряжения получим, разделив значение этой силы на площадь поперечного сечения трубки A = :

.

После определения напряжений в стенках трубки от каждого внешнего силового фактора следует провести анализ возникающего напряженного состояния в точках рассматриваемого поперечного сечения 1–1 (см. рис.3.7,с).

Анализ напряженного состояния материала трубки

В рассматриваемом поперечном сечении трубки 1-1 касательные и нормальные , напряжения одинаковы во всех точках, а нормальные напряжения от изгибающего момента достигают экстремальных значений в точках С и В сечения. Значит опасными точками могут быть точки С и В (рис.3.7,е).

Точка С. Нормальные напряжения:

по оси трубки 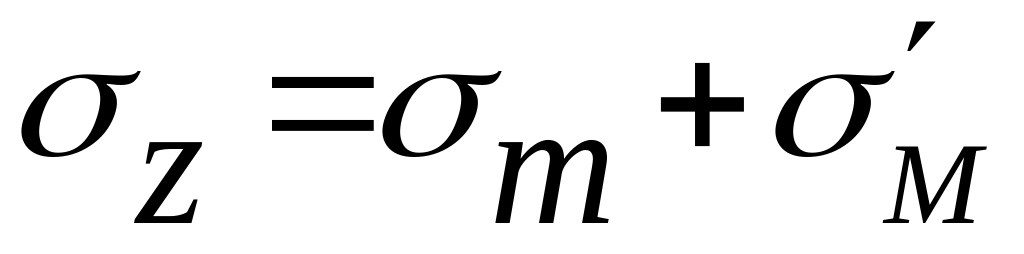= 25+20 = 45МПа.

В тангенциальном направлении = 50МПа.

Касательные напряжения: = 10МПа.

Точка В. Нормальные напряжения:

по оси трубки = 25-20 = 5МПа,

в тангенциальном направлении = 50МПа.

Касательные напряжения: = 10МПа.

Напряженное состояние рассматриваемых элементов точек – двухосное, т.к. напряжения в радиальном направлении можно принять . Сравнение полученных величин напряжений показывает, что наиболее опасной точкой поперечного сечения трубки является точка С. Максимальное и минимальное нормальные напряжения в главных площадках для этой точки находятся по формуле (см. пример решения задачи №1, п. 3.1):

=(47.5± 10.3)МПа,

или

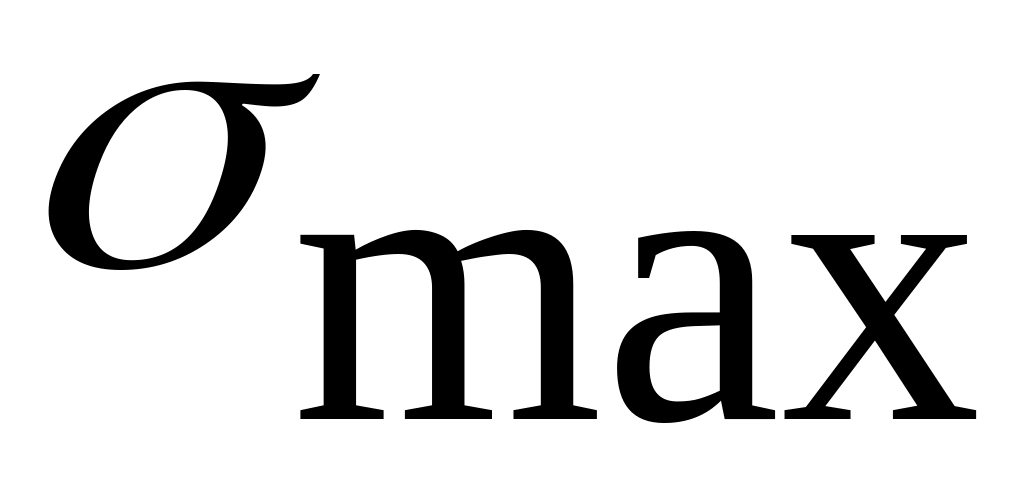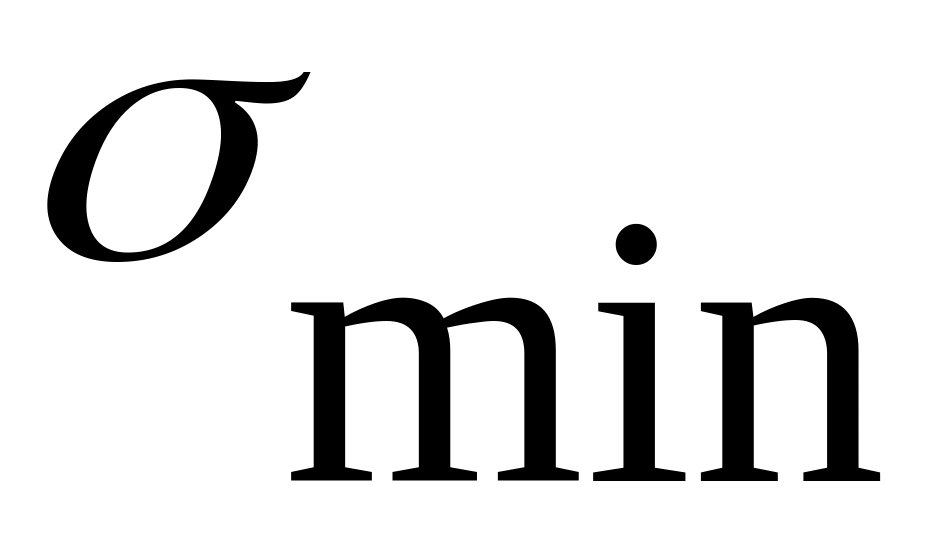= 57.8МПа, = 37.2МПа.

Главные напряжения для рассматриваемого элемента записываются в алгебраическом порядке ( ) следующим образом:

= 57.8МПа, = 37.2МПа , = 0.

Учитывая заданный материал трубки ( ), находим эквивалентное напряжение для рассматриваемой точки по теории прочности Мора (3.3):

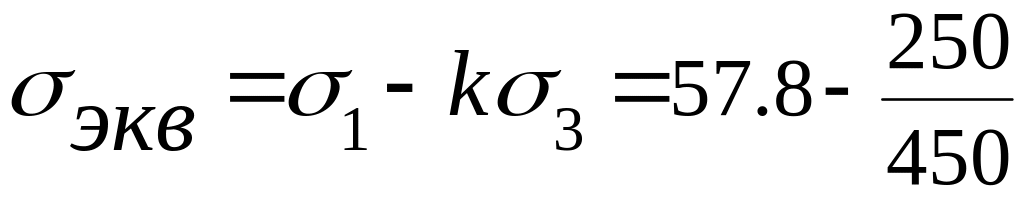·0 = 57.8МПа.

Определение коэффициента запаса

Из выше проведенных расчетов следует, что наиболее опасной точкой поперечного сечения трубки является точка С. В ней

= 57.8МПа.

Коэффициент запаса по текучести в этой точке определим по следующей формуле:

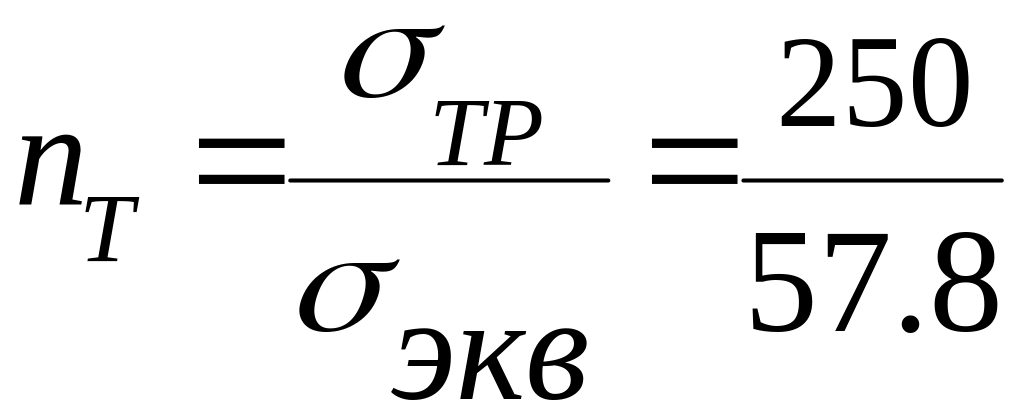= 4.33.

Если нельзя сразу указать опасную точку сечения, то следует провести расчет коэффициента запаса для каждой из точек С и В отдельно и выбрать из них наименьший.

Расчет вала на статическую прочность

и сопротивление усталости

В данной задаче студент должен решить вопросы, которые составляют следующие три раздела:

- проектировочный расчет вала на статическую прочность;

- конструирование вала;

- проверочный расчет вала на усталостную прочность.

4.1. Проектировочный расчет вала на статическую прочность

При расчете вала (рис. 4.1, а) на статическую прочность он пред-ставляется в виде двухопорной балки, нагруженной постоянными скручивающими и изгибающими моментами, поперечными и продольными усилиями от деталей, установленных на валу (рис. 4.1, б). Одна из опор выбирается шарнирно – неподвижной, другая – шарнирно-подвижной (плавающей). Это обеспечивает свободную осевую деформацию вала и делает конструкцию статически определимой. Если по условиям работы вала безразлично какая из опор будет закреплена, то в качестве плавающей опоры следует выбирать более нагруженную.

При определении нагрузок, действующих на вал, установленные на нем детали (колеса) мысленно отбрасывают и их действие на вал заменяют соответствующими нагрузками, определяемыми по известным правилам теоретической механики (рис. 4.1, в, г, д). Векторы радиальных сил F_У переносят на вал вдоль линии их действия, векторы окружных F_X и осевых F_Z усилий – параллельно самим себе. При этом от сил F_X появляются скручивающие T = F_X·R , а от F_Z – изгибающий M = F_Z·R моменты (R – радиус начальной окружности колеса). Найденные нагрузки представляются в виде составляющих в трех взаимно перпендикулярных плоскостях (вертикальной XY, горизонтальной ZX и поперечной XY).

Таким образом, вал работает на совместное действие растяжения (сжатия), кручения и изгиба, причем изгиба в двух плоскостях(ZY и ZX).Влиянием растяжения (сжатия) и поперечных сил на нагруженность вала пренебрегают.

4.1.2. Построение эпюр внутренних силовых факторов

Используя метод сечений и известные правила, строят эпюры:

-изгибающих моментов M_X(Z) и M_Y(Z) в вертикальной (ZY) и горизонтальной (ZX) плоскостях соответственно:

- суммарного изгибающего момента;

; (4.1)

- крутящего момента T_К(z);

- эквивалентного изгибающего момента М_ЭКВ(z) по гипотезе прочности максимальных касательных напряжений

. (4.2)

4.1.3. Расчет диаметра вала

Для заданной конструкции вала (см. рис. 4.1, а) наибольшие значения эквивалентного изгибающего момента могут возникать в сечениях А и С. Если построить эпюры напряжений в опасном сечении (рис. 4.2), то элемент опасной точки К будет находиться в условиях плоского напряженного состояния (рис. 4.2, в). Условие прочности должно быть записано на основе одной из гипотез (теорий) прочности. В соответствии с условием задачи следует использовать гипотезу прочности максимальных касательных напряжений, что было учтено при записи формулы (4.2).

Условие прочности запишем в виде

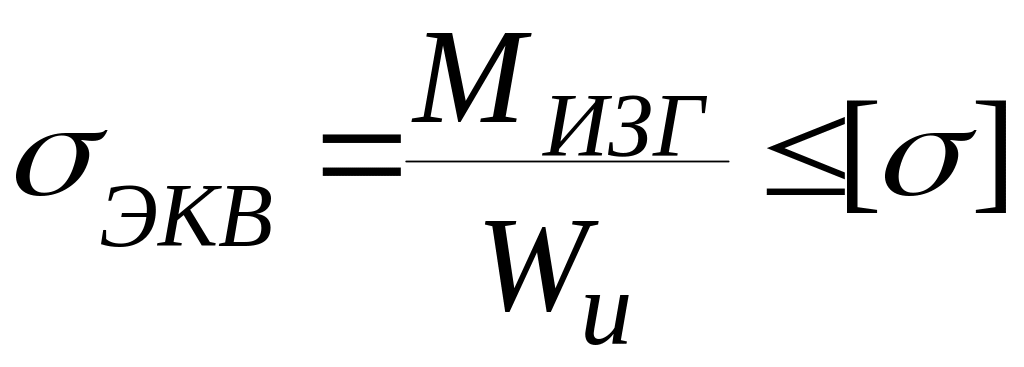. (4.3)

Где [ ] –допускаемое напряжение для вала, назначаемое по табл. П.1 (см.приложение 1);

W_И – момент сопротивления изгибу.

Для вала круглого сплошного поперечного сечения 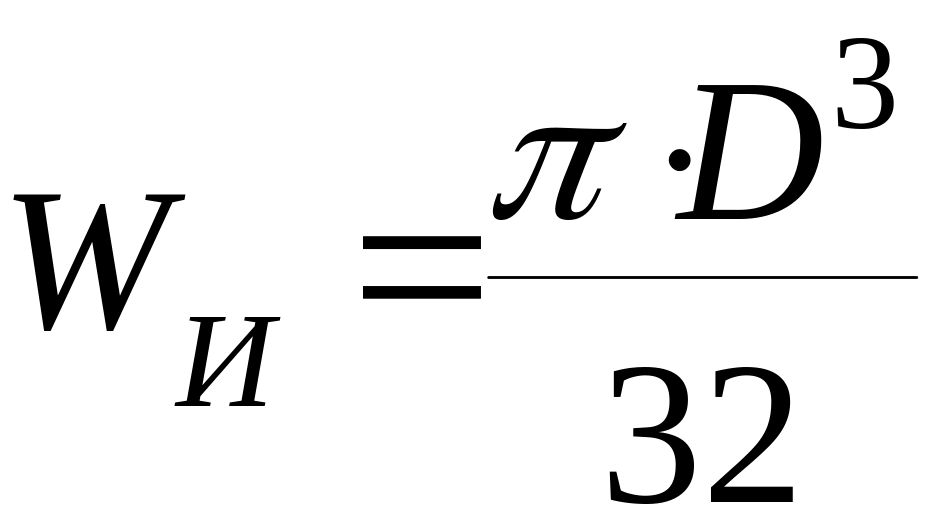, тогда из (4.3) минимально допустимое значение диаметра вала

. (4.4)

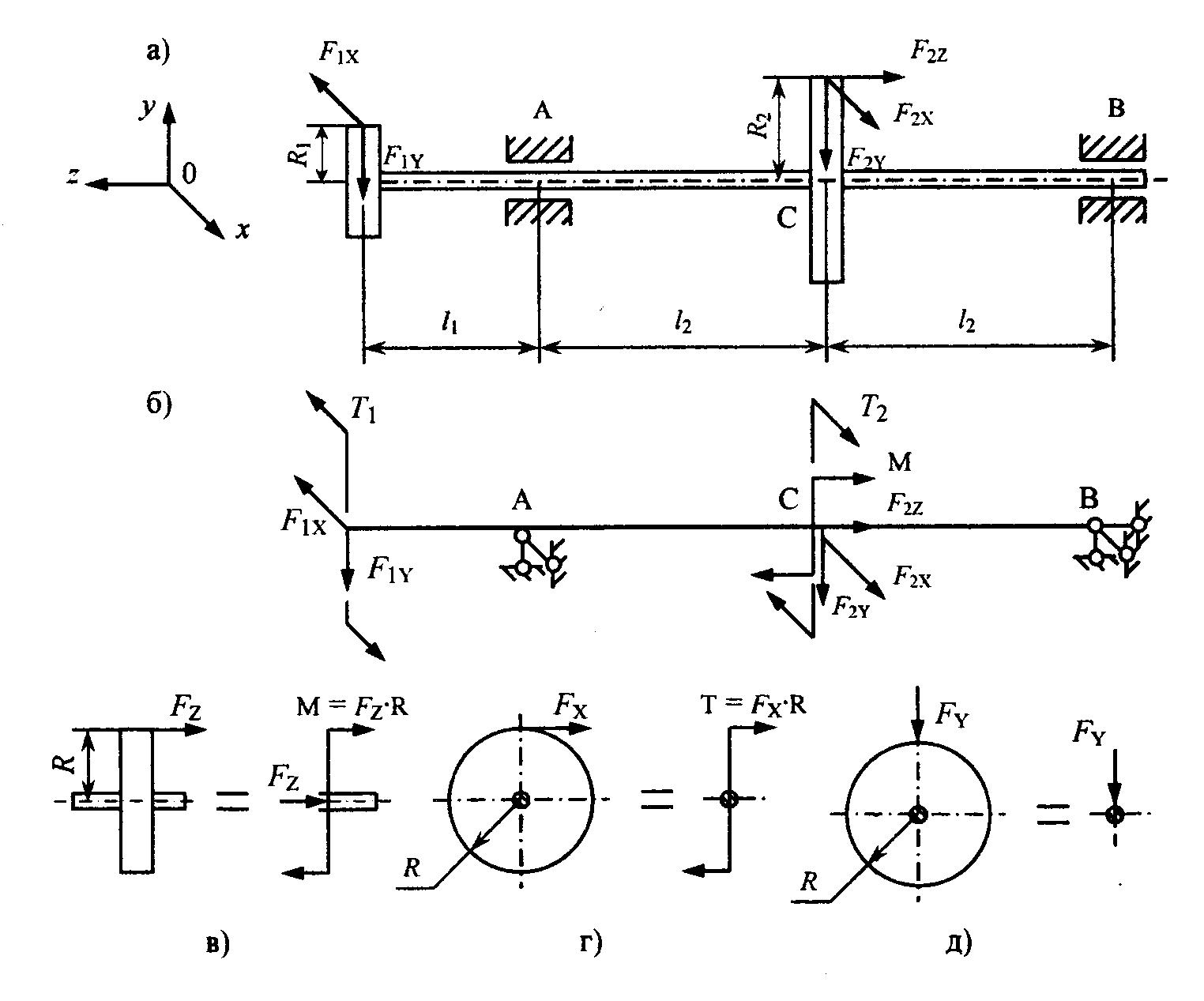
Рис. 4.1

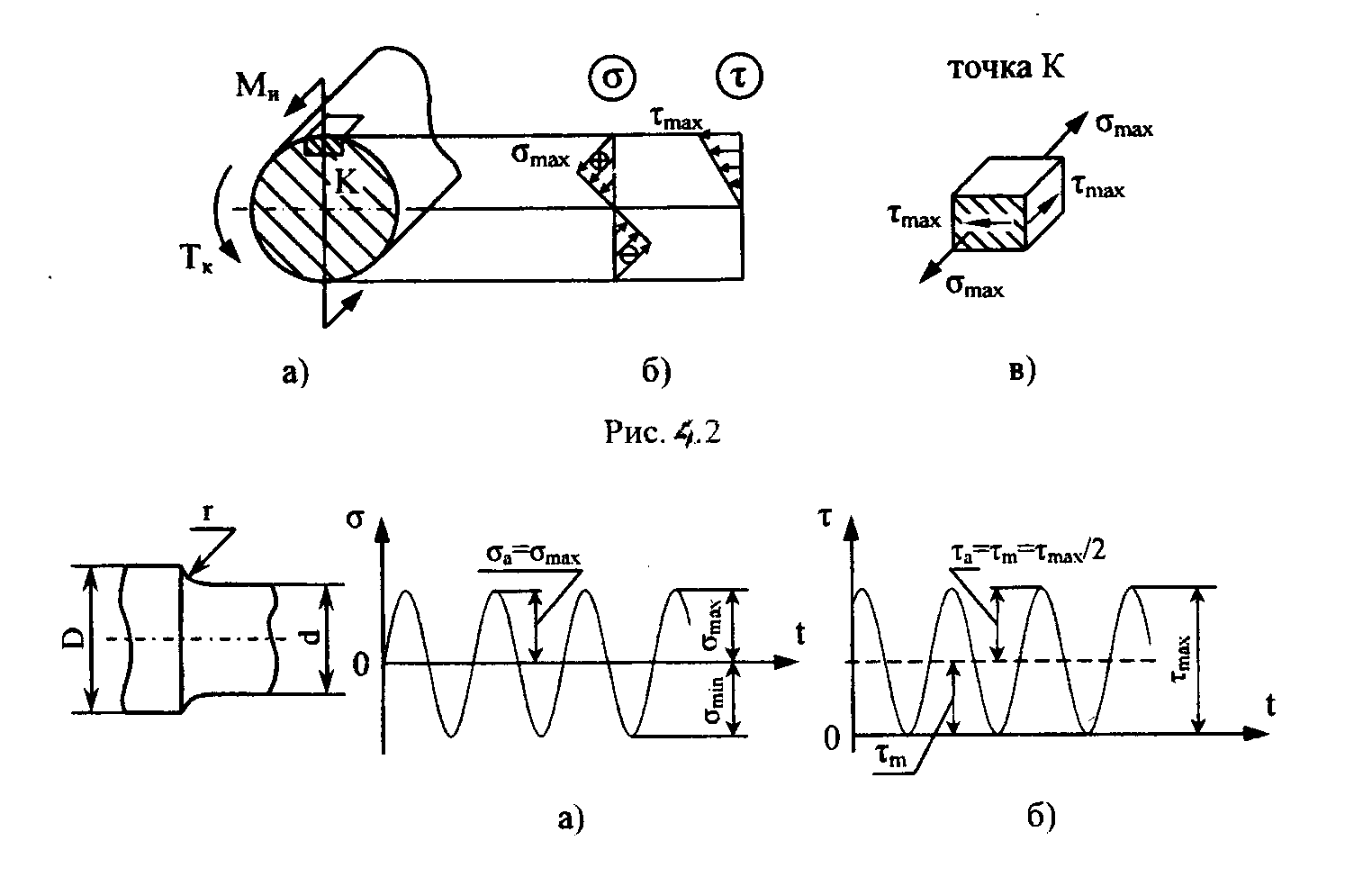
Рис. 4.3 Рис. 4.4

Диаметр D₂ в месте установки шестерни 2 (см. схему вала) следует округлить до ближайшего большего числа из стандартного ряда (ГОСТ 6636-86), включающего в себя следующие размеры: 16, 17, 18, 19, 20, 21, 22, 24, 25, 26, 28, 30, 32, 33, 34, 36, 38. 40, 42, 45, 48, 50, 52, 53, 55, 60, 63, 65, 70, 75, 80, 85, 90, 95,, 100 мм и далее через 10 мм.

Значение диаметра D₁ в месте установки подшипников нужно округлить до ближайшего числа, оканчивающегося на 0 или 5 (согласование со стандартным рядом посадочных диаметров подшипников [ 8 ]).