1.1.2 Робота виходу електронів. Електронна емісія

При температурі абсолютного нуля (Т = 0⁰К) і відсутності других джерел збудження електрони в атомах будь-якої речовини займають рівні з найменшою енергією.

N = f(W) Із графіка видно, що при температурі

абсолютного нуля немає електронів,

які мають енергію, більшу W_F (рівень

1 Фермі).

Рис. 1.3. Графік розподілення електронів за величинами

W_F W енергії в зоні провідності

Величина W_F залежить від фізичних властивостей матеріалу:

, (1.5)

де h - постійна Планка,

m_e - маса електрона,

N - число вільних електронів в 1 см³ провідника. В металах N≈10²²...10²³.

Енергія Фермі W_F має досить велике значення. Чому ж немає виходу електронів за поверхню металу?

По-перше. Ті електрони, які виходять за межу провідника, втрачають більшу частину своєї енергії і накопичуються на поверхні металу. Між цими електронами та додатніми іонами, які знаходяться всередині металу біля його поверхні, утворюється електричне поле, ж направлене від провідника до шару електронів. Дія подвійного електричного шару на електрони, які намагаються залишити межі металу, є гальмівною, т.я. електронам приходиться літати в напрямку електричних силових ліній і віддавати енергію полю.

По-друге. Метал, який залишився без частини електронів, заряджається позитивно і, таким чином, між ним і електронами виникає електричне поле, яке закриває вихід нових електронів.

Таким чином, для відриву від поверхні провідника електрони повинні затратити роботу проелектричних сил, які повертають їх назад:

W_a = W_F + W₀, (1.6)

Вихід електронів можливий також із напівпровідників та діелектриків. Але при цьому робота витрачається не лише на подолання гальмових електричних сил, але й на збудження електронів, які переходять із валентної зони в зону провідності.

Таким чином, якщо електронам металів або напівпровідників повідомити із зовні додаткову енергію, то вихід їх із тіла стає можливим. Процес надання електронам додаткової енергії для їх виходу з речовини називається електронною емісією.

В залежності від способу повідомлення електронам додаткової енергії електронна емісія буває:

• термоелектронна - при якій додаткова енергія повідомляється в результаті нагріву катода;

• фотоелектронна - під дією електромагнітного випромінювання;

• електростатична - сильне електричне поле біля поверхні речовини створює сили, які допомагають електрону вийти за її межі.

1.1.3 Рух електронів в електричних та магнітних полях

Електрон в електричному полі. На електрон, який поміщений в електричне поле з напруженістю Е, діє сила, яка дорівнює:

F = -eE, (1.7)

де E - напруженість поля в місці знаходження заряду;

е - заряд електрона.

Знак “-“ показує, що внаслідок негативного заряду електрона сила має напрям протилежний напряму вектора напруженості електричного поля.

₂ U₄ F U₄ υ₁

U F U₃ U₃

υ₀ U₂ ² υ₀ U₂ υ₀

- ¹ U₁ U₁

а) б) в)

Рис. 1.4. Рух електрона в прискорюючому (а), гальмівному (б) і поперечному (в) електричних полях

На рисунку 1.4,а показане однорідне електричне поле, яке побудоване між двома паралельними пластинами достатньо великої протяжності. Під дією сили F електрон рухається назустріч електричному полю (переміщується в сторону точок з більш високим потенціалом). Поле в даному випадку прискорююче.

Робота, яку поле затрачає на переміщення заряду із однієї точки в іншу, визначається за формулою:

А = еU = e(U₃ – U₁), (1.8)

де U - різниця потенціалів між точками 1 і 2,

е - заряд електрона.

Ця робота витрачається на повідомлення електрону кінетичної енергії:

(1.9)

де υ₀ і υ – швидкість руху електрона в точках 1 і 2. Прирівнявши рівності (1.8) і (1.9), отримуємо:

(1.10)

Визначимо кінцеву швидкість електрона в прискорюючому електричному полі при нульовій початковій швидкості (υ₀ = 0).

Із виразу (1.10) отримаємо:

(1.11)

Якщо підставити в (1.11) значення заряду і маси електрону, можна отримати вираз для швидкості електрону (км/с):

(1.12)

Таким чином, швидкість, яку отримує електрон при рухові в прискорюючому електричному полі, залежить лише від пройденої ним різниці потенціалів.

Із формули (1.12) видно, що швидкості електронів, навіть при порівняно невеликій різниці потенціалів, получаються значними. Наприклад, при U=100 В отримуємо . При такій великій швидкості всі процеси в приладах, пов̕язані з рухом електронів, протікають дуже швидко. Наприклад, час, необхідний для пролітання електронів між електродами в електронній лампі, складає долі мікросекунди. Саме тому робота більшрсті електронних приладів може вважатись безінерційною.

Розглянемо рух електрона, у якого початкова швидкість направлена проти сили, яка діє на електрон зі сторони електричного поля (рис.1.4,б). В цьому випадку електричне поле є для електрона гальмуючим. В той момент, коли електрон повністю витратить свою енергію, його швидкість буде дорівнювати нулю, і потім електрон почне рухатися в зворотному напрямі. Рух його в зворотньому напрямі є нічим іншим, як розглянутий вище рухом без початкової швидкості в прискорюючому полі. При такому русі електрону поле повертає йому ту енергію, яку він витратив при гальмуючому русі.

В розглянутих вище випадках напрям швидкості руху електрону було паралельним напряму силових електричних ліній поля. Таке електричне поле називається продольним. Поле, направлене перпендикулярно вектору початкової швидкості електрону, називається поперечним. Коли електрон влітає в електричне поле з деякою початковою швидкістю υ₀ і під прямим кутом до напрямку електричних силових ліній (рис.1.4, в), він здійснює одночасно два взаємоперпендикулярних рухи: прямолінійне рівномірне за інерцією із швидкістю υ₀ та прямолінійне рівномірноприскорене із швидкістю υ₁. під дією цих двох взаємоперпендикулярних швидкостей електрон буде рухатися по траекторії, яка являє собою параболу. Після виходу із електричного поля електрон буде рухатися за інерцією прямолінійно.

І снує подібність між законами руху електронів в електричному полі і законами світлової оптики. На основі такої аналогії науку, яка вивчає рух електронів в електричному полі, називають електронною оптикою.

Електрон в магнітному полі. Вплив магнітного поля на рухомий електрон можна розглядати за формулою:

F = Beυsinα (1.13)

Із (1.13) видно, що електрон, який рухається вздовж силових ліній магнітного поля (а = 0), не відчуває ніякого впливу поля (F = B e υ sinα = 0) і продовжує рухатись з заданою йому швидкістю.

Якщо вектор початкової швидкості електрона перпендикулярний вектору магнітної індукції, тобто (рис. 1.5), то сила, яка діє на електрон,

(1.14)

Напрям цієї сили визначається за правилом лівої руки.

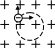
Рис. 1.5. Траєкторія руху електрона в магнітному полі

Сила F завжди перпендикулярна напряму миттєвої швидкості υ електрона і напряму магнітних силових ліній поля. У відповідності з другим законом Ньютона ця сила повідомляє електрону з масою m_e прискорення, рівне . Оскільки прискорення перпендикулярне швидкості υ, то електрон під дією цього нормального прискорення буде рухатися по колу, яке лежить в площині, перпендикулярній силовим лініям поля.

В загальному випадку початкова швидкість електрона може бути не перпендикулярна до магнітної індукції, тобто . В даному випадку траєкторію руху електрона визначають дві складові початкової швидкості: нормальна υ₁ і дотична υ₂, перша із яких направлена перпендикулярно до силових ліній магнітного поля, а друга — паралельно їм. Під дією нормальної складової електрон рухається по колу, а під дією дотичної - перемішується вздовж силових ліній поля.

В результаті одночасної дії обох складових траєкторія руху електрона приймає вигляд спіралі.

Z

υ₁ υ

B

υ₂

X

Y

Рис.1.6. Траекторія руху електрона в магітному полі при