1.Вопрос

1. Производная функции, ее геометрический и механический смысл. Производная суммы, произведения и частного.

Механический смысл производной

Пусть материальная точка движется прямолинейно и - длина пути, проходимого за время , отсчитываемого от некоторого момента времени .

Для определения скорости в данный момент придадим переменной некоторое приращение , при этом приращение пути будет равно .

Отношение называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени , и обозначается

Предел называется величиной мгновенной скорости движения в момент времени .

Таким образом, мгновенная скорость в момент времени прямолинейного движения, совершаемого по закону равна значению производной .

Геометрический смысл производной

Пусть функция определена в некоторой окрестности токи , непрерывна в этой точке и , а (рис.2).

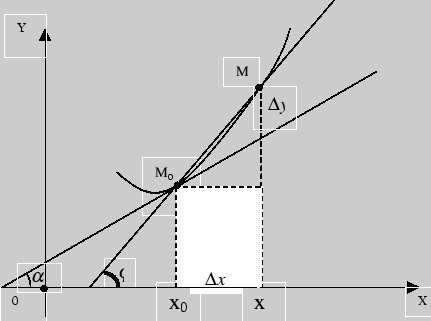
Рис. 2

Придав произвольное приращение аргументу , так чтобы , перейдем к точке с абсциссой и ординатой , где .

Уравнение прямой, проходящей через точки и (секущей графика функции , имеет вид: , где отношение представляет собой угловой коэффициент секущей ( .

Касательной к графику функции в точке называется предельное положение секущей , при стремлении точки по графику к точке .

Для того, чтобы секущая при стремилась к предельному положению, отличному от вертикальной прямой , необходимо и достаточно, чтобы существовал конечный предел , то есть , чтобы существовала конечная производная функции в точке .

Угловой коэффициент касательной получается путем перехода от к пределу при :

2.Вопрос

2. Уравнение касательной и нормали к плоской кривой. Производная сложной функции. Производная обратной функции. Производная элементарной функции. Таблица производных.

Уравнение касательной : y = f(a) + f '(a)(x – a)

Нормали к кривой : Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в данной точке

Производная сложной функции "Двухслойная" сложная функция записывается в виде

где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.

Производная обратной функции.

Для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции, т.е

3.Вопрос

3. Дифференцируемость функции. Непрерывность дифференцируемой функции. Дифференциал функции. Связь с производной.

Дифференцируемость функции

Определение. Если функция y = f(x) имеет производную в точке x = x0, то функция дифференцируема в этой точке..

Непрерывность дифференцируемой функции

   Если функция y = f (x) имеет производную в точке х = х₀, то говорят, что при данном значении аргумента х = х₀ функция дифференцируема.    Если функция дифференцируема в каждой точке интервала (a, b), то говорят, что она дифференцируема на этом интервале.    Если функция дифференцируема в некоторой точке х = х₀, то она в этой точке непрерывна.

Дифференциал функции

Определение. Дифференциалом функции (обозначается через ) называется следующее выражение:

где dx -- дифференциал x при условии, что функция имеет производную.