
- •3. Достаточные признаки сходимости рядов с положительными членами (сравнения, Даламбера, Коши).
- •3) В случае ответа о сходимости или расходимости ряда теорема не дает.
- •4. Знакочередующиеся ряды. Признак Лейбница.
- •5. Знакопеременные ряды. Теорема о сходимости знакопеременного ряда.Абсолютная и условная сходимость знакопеременных рядов. Свойства абсолютно сходящихся рядов.
- •6. Функциональные ряды. Сходимость и сумма ряда. Область сходимости.
- •7. Равномерная сходимость функциональных рядов. Признак Вейерштрасса.
- •Признак равномерной сходимости.
- •1) Признак Вейерштрасса (мажорантный признак)
- •8. Интегрирование и дифференцирование функциональных рядов.
- •9. Степенные ряды. Теорема Абеля. Радиус сходимости. Вычисление радиуса
- •10.Ряды Тейлора и Маклорена.
- •11.Достаточные условия разложения функции в ряд Тейлора.
- •13.Применение степенных рядов к вычислению интегралов, значений функций, решению ду.
- •Приближенное решение ду с помощью степенных рядов
- •1.Способ последовательного дифференцирования
- •2.Способ неопределенных коэфф.
- •14. Тригонометрическая система функций и ее свойства.
- •15. Тригонометрический ряд. Сходимость. Ряд Фурье. Коэффициенты Фурье.
- •20.Приближение в среднем функции тригонометрическими полиномами.
- •21.Неравенство Бесселя.
- •22.Интеграл Фурье. Синус и косинус преобразование Фурье.
- •23.Ряд Фурье в комплексной форме.
- •24.Интеграл Фурье в комплексной форме.
- •25.0Пределение и область существования функции комплексной переменной (фкп).
- •26.Предел и непрерывность фкп.
- •27.Дифференцирование фкп.
- •27.Дифференцирование фкп
- •28.Геометрический смысл модуля и аргумента производной фкп.
- •29.Аналитичность фкп. Условия Коши-Римана.
- •30.Интегрирование фкп.
- •3L.Интегральная формула Коши.
- •32.Степенные ряды фкп. Радиус и круг сходимости.
- •34.Ряд Лорана и область его сходимости.
- •35.0Собые точки и их классификация.
- •36.Вычеты фкп.
- •37.Применение вычетов к вычислению интегралов.
3L.Интегральная формула Коши.
. Формула Коши связывает значение аналитической функции внутри области с граничными точками .
Пусть область -односвязная с границей , -аналитическая функция. Если -внутренняя точка бласти
![]() (инт.
Формула Коши для односвязной области)
(5)
(инт.
Формула Коши для односвязной области)
(5)
Док-во:
Пусть
есть внутренняя точка области
,
тогда функция
![]() аналогична
в области
всюду, кроме точки
аналогична
в области
всюду, кроме точки
![]() .
.
Проведем
круг с радиусом
![]() с центром в
с центром в
![]()
По теореме Коши для многосвязной области
![]()
![]()
-функция
непрерывная, потому, взяв
![]()
![]()
![]() -произвольно
малое число, то
-произвольно
малое число, то
![]()
![]()
![]() .
.
32.Степенные ряды фкп. Радиус и круг сходимости.
Степенной ряд-ряд вида (1)
(1):![]() ,где
С- постоянные комплексные числа.
,где
С- постоянные комплексные числа.
Если
a=0 то (2):![]() ,подстановкой
z-a=t
можно перейти от (1) к (2).
,подстановкой
z-a=t
можно перейти от (1) к (2).
Т.Абеля:
Если ряд (2) сходится абсолютно при z=z0,
то он сходится абсолютно и при всех
|z|<|z0|.
Если ряд (2) расходится при
![]() ,
то он расходится и при всех z
,
то он расходится и при всех z
![]() .
.
Радиус сходимости:
|z-a|=R-круг включая границы
|z-a|<R-круг без границы
Область сходимости степенного ряда - круг. На границе исследовать дополнительно.
ЗЗ. Ряд Тейлора ФКП.
![]() при а=0 ряд Маклорена
при а=0 ряд Маклорена
Теорема: f(z), аналитическая внутри круга с центром в точке z=a разлагается в ряд Тейлора.
Доказательство:
По формуле Коши
![]()
z=a – центр окружности, тогда |z-a|=r(радиус центра) причем

r <σ. Т.к. t-a=σ |t-a|>|z-a| - сумма бесконечно
![]()
убывающей геометр. прогрессии, т.к.. Преобразуем:
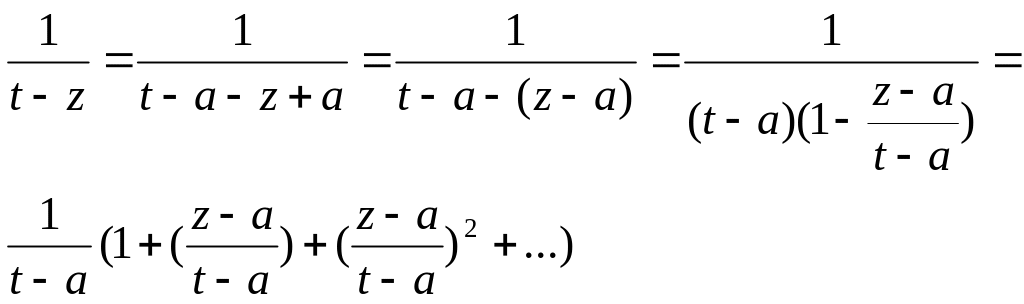
По свойству интегралов: интеграл от суммы ( ∑ ) = сумме интегралов.
Тогда

![]()
34.Ряд Лорана и область его сходимости.
Ряд
Лорана по степеням
![]() - это формула вида
- это формула вида

Правильная
часть ряда Лорана сходится в круге
![]()
Главная
часть ряда Лорана сходится в круге
![]() ,
где
,
где
![]() - внешность круга.
- внешность круга.
![]() .
Если выполняется это условие, то ряд
Лорана сходится в кольце
.
Если выполняется это условие, то ряд
Лорана сходится в кольце
![]() .
.
Теорема
Лорана. Пусть функция
является аналитической в кольце
.
Тогда
![]() ,
где
,
где
![]() - ряд Тейлора по степеням
.
Полученное разложение функции однозначно.
- ряд Тейлора по степеням
.
Полученное разложение функции однозначно.
35.0Собые точки и их классификация.
Число
а наз. нулем ф-ции f(z),
если f(a)=0.
Пусть ф-ция f(z)
аналитична в некоторой окрестности
точки а, тогда для нее имеет место
разложение
![]() .
.
Если
z=a ноль
ф-ции f(z),
то из разложения видно f(а)=C0=0.
Будем говорить, что точка z=a
явл. Нулем порядка k ф-ции
f(z), если
коэффициенты С0, С1, … ,Ск-1
равны 0, а Ск отличен от нуля.
Тогда f(z)=Ск(z-a)k
+… + Cn(z-a)n
+… . При к=1 ноль первого порядка наз.
простым нулем. Точка z=0
явл. Нулем второго порядка. Для того,
чтобы точка z=a
была нулем порядка к ф-ции f(z)
необходимо и достаточно выполнение
соотношения f(а)=0,
![]() а
f(к)(а)0.
Нули ф-ции f(z)=0
наз. изолированными, если их можно
окружить непересекающимися окрестностями.
Для аналитической ф-ции нули явл.
изолированными.
а
f(к)(а)0.
Нули ф-ции f(z)=0
наз. изолированными, если их можно
окружить непересекающимися окрестностями.
Для аналитической ф-ции нули явл.
изолированными.
Полюсы.
Предположим, что f(z) аналитична в окрестности z=a, кроме самой точки а, в этом случае точка z=a явл. Изолированной особой точкой ф-ции. В окрестности этой точки f(z) разлагается в ряд Лорана.
Пусть
все С-n равны
нулю, тогда. Если перейти к пределу,
![]() ,
но в самой точке ф-ция неопределена. В
этом случае точку а наз. устранимой
особой точкой ф-ции f(z).
,
но в самой точке ф-ция неопределена. В
этом случае точку а наз. устранимой
особой точкой ф-ции f(z).
Пусть
в главной части ряда Лорана имеется
конечное число (к) слагаемых, тогда точка
z=a наз.
полюсом к-ого порядка.
![]()
![]()
![]() .
При z=a С-к0.
правую часть обозначим (z).
Функция (z)
явл. Аналитической ф-цией всюду, кроме
точки z=a.
.
При z=a С-к0.
правую часть обозначим (z).
Функция (z)
явл. Аналитической ф-цией всюду, кроме
точки z=a.
![]() ,
где (z)0
,
где (z)0
![]() .
Если для ф-ции f(z)
z=a полюс
к-ого порядка, то для ф-ции
.
Если для ф-ции f(z)
z=a полюс
к-ого порядка, то для ф-ции
![]() ,
(а)0,
есть ноль к-ого порядка. Справедливо и
обратное: если для ф-ции
,
(а)0,
есть ноль к-ого порядка. Справедливо и
обратное: если для ф-ции
![]() z=a
полюс к-ого порядка, (а)0.
z=a
полюс к-ого порядка, (а)0.
Полюсы также явл. Изолированными особыми точками.
Если в разложении (1) главная часть содержит бесконечное число слагаемых, т точка z=a наз. существенно особой точкой.
