Прямые доказательства

Доказательства делятся на прямые и косвенные. Прямым называется такое доказательство, в котором тезис обосновывается непосредственно аргументами. Если для доказательства тезиса приводятся аргументы, из которых непосредственно вытекает истинность, или, наоборот, ложность данного тезиса, то такое доказательство является прямым.

Схема этого доказательства такова: из данных аргументов (а, в, с...) необходимо следует доказываемый К. По этому типу проводится доказательство в науке, в полемике, в судебной практике и т.д. Прямое доказательство находит широкое применение в статистических отчетах, в различного рода документах, в постановлениях, художественной и мемуарной литературе, обучении. Например, на занятиях по социальной философии при доказательстве тезиса: "Народ - решающая сила исторического процесса" преподаватель, во-первых, показывает, что народ является создателем материальных благ; во-вторых, обосновывает его значительную роль в политической сфере; в-третьих, раскрывает его вклад в создание духовных ценностей общества.

Таким образом, при прямых доказательствах задача состоит в том, чтобы найти убедительные аргументы, из которых логически вытекает тезис.

Косвенные доказательства

Косвенным называется такое доказательство, которое устанавливает истинность доказываемого тезиса, исследуя не сам тезис, а некоторые другие положения. Эти положения так связаны с доказываемым тезисом, что из установления их ложности необходимо вытекает истинность доказываемого тезиса. В косвенном доказательстве поэтому задача состоит в выяснении ложности положений, обусловливающих истинность доказываемого тезиса.

Косвенные доказательства бывают двух видов: апагогические и разделительные. В апагогическом доказательстве к истинности тезиса приходят путем доказательства ложности антитезиса. Антитезисом называется суждение, противоречащее тезису.

Апагогическое доказательство проходит следующие этапы: выдвигается антитезис, и из него выводятся следствия с намерением найти среди них хотя бы одно ложное; устанавливается, что в числе следствий действительно есть ложное; делается вывод, что антитезис неверен; из ложности антитезиса на основании закона исключенного третьего делается заключение, что выдвинутый тезис является истинным.

Косвенное апагогическое доказательство называют еще сведением к абсурду. Например, в романе И.С. Тургенева "Рудин" есть такой диалог:

"...Стало быть, по-вашему, убеждений нет?

- Нет - и не существует. - Это ваше убеждение?

-Да.

- Как же вы говорите, что их нет? Вот вам уже одно, на первый случай".

Ошибочному мнению, что никаких убеждений нет, противопоставляется его отрицание: есть по крайней мере одно убеждение, что убеждений нет. Коль скоро утверждение "Убеждения существуют" вытекает из своего собственного отрицания, то это убеждение, а не его отрицание, является истинным и доказанным.

Если число рассматриваемых возможностей не ограничивать двумя (доказываемым утверждением и его отрицанием), то это будет так называемое косвенное разделительное доказательство. Его сущность состоит в том, что доказываемый тезис рассматривается как одно из некоторого числа предположений, в своей сумме исчерпывающих все возможные по данному вопросу предположения. Разделительное доказательство применяется в тех случаях, когда можно быть уверенным, что доказываемое положение входит в число всех рассматриваемых возможностей. Антитезис является одним из членов разделительного суждения, в котором должны быть обязательно перечислены все возможные альтернативы.

Например:

Преступление могли совершить только либо А, либо В, либо С.

Доказано, что не совершали преступление ни А, ни В

Преступление совершил С

Истинность тезиса устанавливается путем последовательного доказательства ложности всех членов разделительного суждения, кроме одного.

Доказательные рассуждения различаются не только по способам аргументации, которые мы уже рассмотрели, но и по своему отношению к выдвинутому тезису. Можно или подтверждать истинность тезиса, или опровергать, доказывать его ложность. Поэтому операция опровержения столь же распространена, как и операция доказательства, и является как бы зеркальным отображением последней.

Доказательство от противного и опровержение. Опровержение тезиса, опровержение аргументов и опровержение демонстрации.

Наиболее распространенным видом косвенных доказательств является доказательство от противного.

В доказательстве от противного обосновывается ложность антитезиса.

Антитезис – суждение, противоречащее тезису.

Если ложность антитезиса обоснована, то согласно закону исключенного третьего, тезис будет истинным суждением.

Доказательство от противного - это апагогическое доказательство (см. предыдущий вопрос).

Логические ошибки в доказательстве.

Нарушение правил логики может относиться к любому элементу структуры рассуждения или доказательства. Если речь идет о дедуктивном рассуждении, то ошибки в нем могут возникнуть, во-первых, из-за отступления или подмены тезиса доказательства. Во-вторых, часто спор из-за доказательства тезиса ошибочно принимается за спор об истинности самого тезиса. В-третьих, в ходе доказательства незаметно подменяются доводы, а иногда используются произвольные или даже ложные доводы. В-четвертых, нередко прибегают к мнимым доказательствам, когда одно суждение доказывают с помощью другого, а последнее, в свою очередь, доказывают с помощью первого. В-пятых, зачастую в процессе полемики допускаются логические противоречия, в силу чего доказательства оказываются несостоятельными. Порой в качестве доводов, служащих посылками для доказательства тезиса, используют суждения, которые по логической силе слабее самого тезиса.

В-шестых, многие ошибки связаны с нечеткостью языка, путаницей в употреблении понятий, подменой смысла суждений, а также заменой логических и фактических доводов психологическими и нравственными.

Приведем основные ошибки по составляющим доказательства.

Ошибки относительно тезиса

1. Подмена тезиса (ignoratio elenchi).

2. Довод к человеку (argumentum adhominem).

3. Довод к публике (argumentum adpopulum).

4. Кто слишком много доказывает, тот ничего не доказывает (qui nimium probat, nihil probat).

Ошибки относительно аргументов

1. Ложный аргумент или основное заблуждение (error funda-mentalis).

2. Предвосхищение основания (petitio principii).

3. Не следует, не вытекает (поп sequitur).

4. От сказанного в относительном, условном смысле к сказанному безотносительно, в абсолютном смысле. Или: от сказанного в принципе к сказанному во всех без исключения случаях.

5. Круг в доказательстве (circulus in demonstrando). Или: тавтология в доказательстве, т. е. то же через то же, повторение того же самого или одного того же (idem per idem).

Ошибки, связанные с демонстрацией

1. Поспешное обобщение.

2. Учетверение терминов.

Всякое нарушение правил логики влечет за собой ошибки в рассуждении независимо от того, сознает ли это участник спора или нет. Но такие ошибки могут быть использованы вполне сознательно для достижения победы в споре. В этом случае их принято называть софизмами. Следовательно, с чисто логической точки зрения принципиального различия между ошибками и софизмами не существует, ибо они имеют единую основу, а именно: нарушение правил последовательного, доказательного рассуждения. Однако психологическое различие остается. Ошибки совершаются непреднамеренно, софизмы же являются преднамеренными, рассчитанными на победу над оппонентом в споре.

Гипотеза: структурные особенности, роль гипотезы в развитии научного знания.

Гипотеза — это закономерная форма развития знаний, представляющая собою обоснованное предположение, выдвигаемое с целью выяснения свойств и причин исследуемых явлений.

Гипотеза — это всеобщая и необходимая для любого познавательного процесса форма развития знаний. Там, где есть поиск новых идей или фактов, закономерных связей или причинных зависимостей, там всегда присутствует гипотеза. Она выступает связующим звеном между ранее достигнутым знанием и новыми истинами и одновременно познавательным средством, регулирующим логический переход от прежнего неполного и неточного знания к новому, более полному и более точному.

Гипотеза представляет собой систему понятий, суждений и умозаключений. При этом в отличие от них структура она носит сложный, синтетический характер. Ни одно отдельно взятое понятие, суждение, умозаключение в своем содержании не составляет еще гипотезы. Обратимся, например, к известной гипотезе академика А.И. Опарина о происхождении жизни на Земле. Ее положения не ограничиваются каким-либо одним суждением, например, о том, что жизнь возникла в воде или началась с появлением сложных надмолекулярных белковых структур. Данная гипотеза, как и любая другая, пытается объяснить процесс возникновения жизни на Земле во всей его сложности. Естественно, что это невозможно сделать одним суждением или умозаключением. Даже более узкая гипотеза, касающаяся какого-либо одного явления, например, гипотеза об авторстве вновь найденной художественной картины, состоит не из одного суждения, а из целой системы суждений и умозаключений, которая обосновывает вероятность выдвинутого предположения. При этом характер таких суждений обосновывается на взглядах различных экспертов (специалистов) в своей отрасли знания.

В структуре гипотезы различают следующие элементы.

Во-первых, основание гипотезы - совокупность фактов или обоснованных утверждений, на которых основывается предположение.

Во-вторых, форма гипотезы - совокупность умозаключений, которая ведет от основания гипотезы к основному предположению.

В-третьих, предположение (или гипотеза в узком смысле слова) - выводы из фактов и утверждений, обосновывающих гипотезу.

Будучи одинаковыми по логической структуре, гипотезы тем не менее различаются по своему содержанию и выполняемым функциям.

Роль метода гипотез в развитии научного знания нашла отражение в гипотетико-дедуктивных теориях, представляющих собой дедуктивно организованные системы гипотез различной степени общности. Такие теории являются неполными, что открывает возможности для их расширения и конкретизации за счет дополнительных гипотез, прикладных моделей. Все это в конечном итоге обеспечивает достаточную широту и гибкость применения гипотез и других развитых форм теоретического знания для отражения сложных объектов и процессов объективной реальности.

Практическое значение логики. Применение дедуктивной логики в обыденной жизни.

Практическое значение логики - повседневное применение. Как ни скромно выглядят простые действия арифметики, по сравнению с высшей математикой, но без них не сделаешь шагу в жизни. Логические законы играют такую же роль: без мышления невозможна даже элементарная деятельность в любой области. Решение - это всегда выбор оптимального пути движения к намеченной цели. Надежность выбора зависит от надежности прогнозов. Решения, принимаемые вслепую или с опорой на интуицию, чреваты самыми неприятными последствиями. Если решение можно свести к однозначному выбору наиболее оптимального варианта, то такая задача решается техническими средствами. От лица, принимающего ответственные решения, ожидают выбора именно тогда, когда решение нельзя считать однозначным, и здесь без знания законов логики не обойтись.

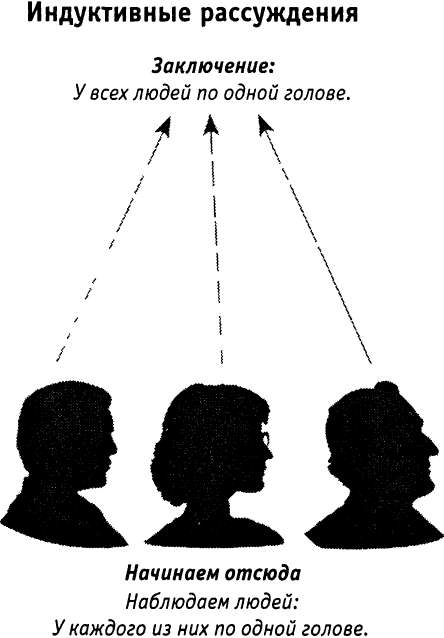
При дедуктивных рассуждениях мы начинаем с утверждений, которые являются или считаются истинными, например «у всех людей только по одной голове», а затем заключаем, что у Ла Тиши, женщины, которую мы никогда не видели, должна быть одна голова. Это заключение логически следует из предыдущего утверждения. Если мы знаем, что утверждение о том, что у всех людей по одной голове, верно, то тогда должно быть верным и то, что у любого конкретного человека имеется только одна голова. Такой вывод неизбежно следует из утверждения; если утверждение верно, то верным должно быть и заключение. Иногда дедуктивные рассуждения описывают, как рассуждения, «нисходящие» от общих представлений о природе мира к конкретным примерам или наблюдениям. Рипс (Rips, 1988) утверждал, что дедукция является общим механизмом, применимым для решения всех когнитивных задач. Он считает, что дедукция «позволяет нам отвечать на вопросы, основываясь на информации, хранящейся в памяти, планировать действия по достижению целей и решать некоторые виды головоломок».

Несмотря на то что между индуктивными и дедуктивными рассуждениями часто проводят разграничение (Neubert & Binko, 1992), оно не имеет большого значения при описании того, как люди рассуждают в действительности. В обыденной ситуации мы переключаемся в процессе мышления с индуктивных рассуждений на дедуктивные и наоборот. Наши гипотезы и убеждения управляют нашими наблюдениями, а наши наблюдения, в свою очередь, приводят к изменению наших гипотез и убеждений. Часто этот процесс представляет собой непрерывное переплетение индуктивных и дедуктивных рассуждений. В действительности мышление почти всегда происходит с применением методов различных типов.

Практическое значение логики. Применение индуктивной логики в науке.

*Практическое значение логики. Применение диалектической логики в общественной жизни

*Принципы и законы диалектической логики. Пример одного из законоы или принципов.