2.3. Исследование нелинейных систем методом фазовой плоскости
2.3.1. Основные понятия
Метод фазовой
плоскости обычно применяется для анализа
нелинейных систем второго порядка при
исследовании в них собственных процессов
или вынужденных при
.
Пусть в нелинейной системе рис. 2.2
передаточная функция имеет вид
. (2.10)
Используем модели (2.7), (2.8) для данного случая и запишем уравнения (2.7) в нормальной форме [1]:
,
.
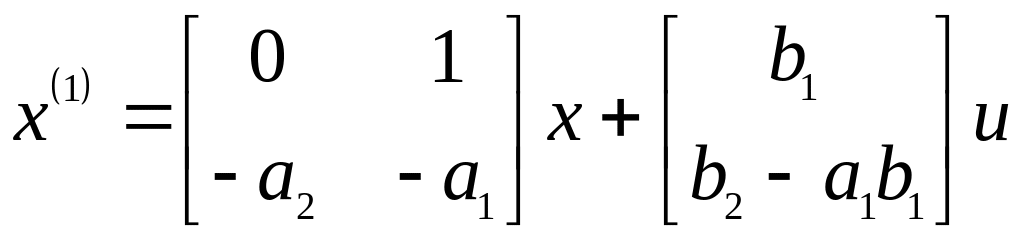Уравнение замкнутой системы (2.8) будет
,
.
Будем полагать,
что
,
а нелинейность обладает свойством
симметрии относительно начала координат
(рис 2.3, 2,4), т.е.
.
В этом случае уравнения примут вид:
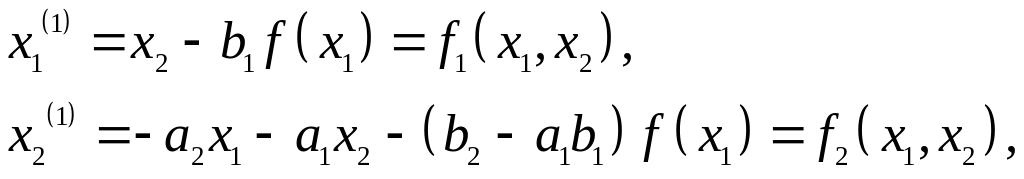(2.11)
где
,
– нелинейные функции.
Частным случаем
уравнения (2.11) является случай, когда
:
(2.12)
который встречается довольно часто.
Характерной
особенностью (2.11), (2.12) является то, что
координата
является скоростью изменения координаты
,
т.е.
.
Пусть при заданных
начальных условиях
,
определено конкретное (частное) решение
уравнения
(2.11). В трехмерном пространстве с
координатами
,
,
это решение можно изобразить в виде
некоторой кривой, которую называют
интегральной
кривой.
Проекция этой кривой на плоскость с
координатами
,
также будет некоторой кривой или
траекторией, которую будем называть
траекторией
состояния
или фазовой
траекторией.
Совокупность фазовых траекторий на плоскости с координатами , будем называть фазовым портретом системы, а саму плоскость – фазовой плоскостью.
При
все вышесказанное можно обобщить, однако
ввиду сложной геометрической интерпретации
фазовое пространство и фазовые траектории
для этого случая применяются редко.
Найдем уравнения,
определяющие фазовые траектории. Для
этого в (2.11) разделим почленно второе
уравнение на первое, тогда с учетом
,
получим
. (2.13)
Уравнение (2.13) является нелинейным дифференциальным уравнением первого порядка, в котором является аргументом (независимой переменной). Решение этого уравнения ( ) и является искомой фазовой траекторией. Так как в конечном итоге координаты и зависят от времени , то с течением времени точка на фазовой траектории, которую назовем изображающей точкой, будет двигаться по фазовой траектории.
Для частного случая (2.12) уравнения фазовых траекторий будут иметь вид
. (2.14)
Правила движения
изображающей точки по фазовым траекториям
на фазовой плоскости
,
где
– ось абсцисс,
– ось ординат:
а) если
,
то по фазовой траектории изображающая
точка движется слева направо в сторону
увеличения
,
т.к. скорость
;
б) если
,
то наоборот – справа налево;
в) ось фазовая траектория пересекает под прямым углом (свойство справедливо только для уравнения (2.14)).
Рассмотрим
качественное соответствие характера
поведения интегральной кривой (координат
,
)
и соответствующих фазовых траекторий.
На рис. 2.3 показаны 5 видов процессов
:
1 − периодический, 2 − возрастающий
колебательный, 3 − затухающий
колебательный, 4 − монотонный
возрастающий, 5 − монотонный
затухающий. На рис. 4 для каждого из
них показаны фазовые траектории.
Рис. 2.3
Рис. 2.4
Итак, если известен
фазовый портрет системы, то можно
качественно оценить характер протекающих
в системе процессов: являются ли они
затухающими и стремятся к нулю при
либо нет; как затухают – с колебаниями,
либо монотонно; являются ли периодическими
и т.п.