VIII. Проецирование контуров отверстий в различных геометрических телах

Приступая к построению проекций контуров отверстий, следует, прежде всего, уяснить:

1) Каким поверхностями образовано отверстие или «пробивающее» его тело, что то же самое (В вашем задании отверстия «пробиваются» призмами, следователь­но, стенки их будут плоскими). Если стенки отвер­стия плоские, сразу уточните положение этих плоскостей от­носительно плоскостей проекций.

2) С какими поверхностями, ограничивающими снаружи и изнутри заданную фигуру, будут пересекаться стенки от­верстия. Здесь же уточните, какого вида линии (прямые, ок­ружности, параболы и т. д.) должны получиться в пересече­нии каждой стенки отверстия с пересекаемыми поверхностя­ми фигуры.

Исходя из выясненного, выбирается метод построения проекций контура отверстия.

Когда стенки отверстия плоские и пересекаются только с плоскостями, контур отверстия будет образован отрезками прямых линий, и его можно строить, определив точки на концах этих отрезков. На рис. 10 показана четырехгранная пирамида с призматическим отверстием. Его контур построен по точкам Е, F, G и Н, представляющим собой точки выхода ребер отверстия на грани пирамиды.

Исходя из того, что контур отверстия задан на фронталь­ной проекции, т. е. заданы фронтальные проекции точек Е₂, G₂ и Н₂, найти их горизонтальные проекции можно одним из указанных в разделе VII способов. Точки лежат на пло­скостях, на которых можно провести прямые через эти точ­ки, отметив затем на их проекциях недостающие проекции точек.

Можно использовать в качестве вспомогательных прямые общего положения, как например, прямая 1—2 для точки Σ, или прямые частного положения, как например, горизонталь H-3 для точки H. Горизонталь H-3 проводилась параллельно горизонтальному ребру ВС. Через точки Е и G была прове­дена горизонтальная плоскость Σ, пересекающая грани по квадрату, подобному основанию. На горизонтальной проекции вспомогательной линии пересечения были отмечены про­екции Е₁ и G₁.

На рис.11 показан прямой круговой конус, с призматиче­ским отверстием. Выясним два исходных положения, о кото-

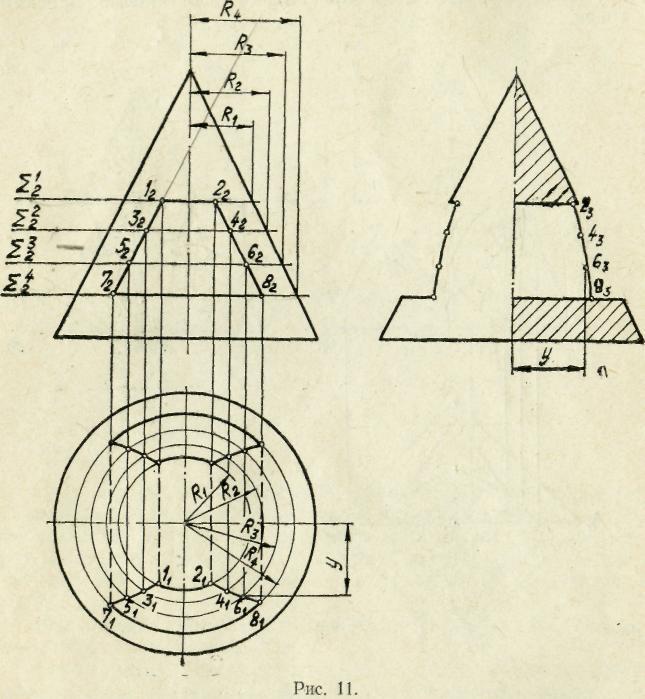
рых говорилось выше. Верхняя и нижняя стенки отверстия представляют горизонтальные плоскости, перпендикулярные к оси конуса и поэтому пересекающие его по окружностям соответствующих радиусов. Боковые стенки являются фрон­тально-проецирующими плоскостями, параллельными контур­ным образующим конуса и поэтому пересекающими его по параболам. Для определения точек, по которым можно будет построить эти параболы, используем вспомогательные секущие плоскости (в данном примере — горизонтальные), так как в пересечении с конусом они, подобно верхней и нижней стенкам отверстия, дадут окружности, проецирующиеся на горизонтальную плоскость проекций в натуральную величи­ну. Плоскости Σ¹ и Σ⁴ образуют на конусе окружности соот­ветственно радиусов R₁ и R₄. На этих окружностях отмечаем точки 1 и 2, 7 и 8. Эти точки будут крайними на участках парабол и они же ограничат входящие в контур отверстия дуги окружностей. Точки 3 и 4, 5 и б, расположенные на па­раболических участках контура, определялись аналогично, с помощью вспомогательных плоскостей Σ² и Σ³.

Профильные проекции всех определяемых точек можно построить по двум другим проекциям, причем опять-таки без введения внешних осей проекций. (Обратите внимание на размер «Y» на рис. 10 и 11).

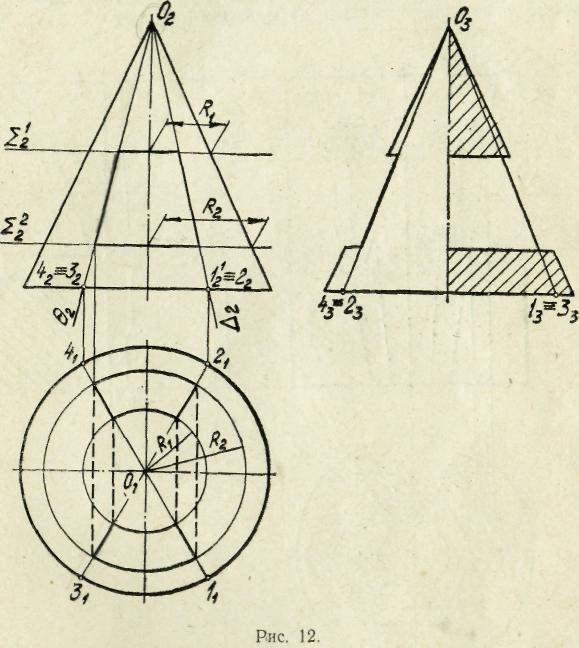
На рис. 12 показан пример, когда контур отверстия обра­зован заведомо известными простыми линиями. Прямой кру­говой конус имеет отверстие, верхняя и нижняя стенки кото­рого горизонтальны и перпендикулярны к оси конуса, как в предыдущем примере, а боковые стенки представляют фрон­тально-проецирующие плоскости, проходящие через вершину конуса. Последнее обстоятельство упрощает построения, так как плоскости, проходящие через вершину конуса, пересека­ют его по прямолинейным образующим. Расширив участки с конусом (плоскости Σ¹ и Σ²), получим в сечениях окружнос­ти соответственно радиусов R₁ и R₂. На этих окружностях по ширине отверстия отметим дуги, входящие в его контур. Сое-

динив концы дуг прямыми, можно получить участки образу­ющих конуса, по которым его пересекают боковые стенки отверстия. Эти же образующие можно построить, расширив участии боковых стенок до полного пересечения конуса (пло­скости и , проходящие через вершину 0). Образующие проходят через точки 1, 2, 3 и 4, в которых плоскости Т и S пересекают основание конуса. Определяются также профиль­ные проекции этих образующих и на них выделяются участ­ки по высоте отверстия.

На рис. 13 показан пример, когда стенки отверстия в пе­ресечении с поверхностями модели образуют контур, в кото­рый наряду с заранее известными простейшими линиями вхо­дят целые заведомо известные участки. Здесь цилиндрическое тело с внутренним вертикальным пирамидальным отвер­стием имеет поперечное призматическое отверстие. Верхняя и нижняя стенки последнего горизонтальны и пересекают на­ружный цилиндр по дугам окружностей, которые на горизон­тальной проекции сливаются с контуром цилиндра. Поверх­ность внутренней пирамиды эти же стенки, если их расши­рить до полного пересечения (плоскости Σ¹ и Σ²), будут пе­ресекать по правильным шестиугольникам, подобным основа­ниям пирамиды. Построения горизонтальных проекций этих шестиугольников показаны на чертеже. В контур отверстия войдут участки шестиугольников, взятые по ширине отвер­стия: 1—-2—3—4 (у верхнего края) и 5—6—7—8 (у нижнего края). Соединив на горизонтальной проекции точки 1 с 5 и 4 с 8, получим прямолинейные участки контура отверстия, образованные пересечением его боковых стенок с гранями пирамиды. Таким образом, будет закончена горизонтальная проекция контура отверстия при его выходе на поверхность внутренней пирамиды. Профильная проекция этого контура строится по двум другим проекциям и будет видна только в разрезе.

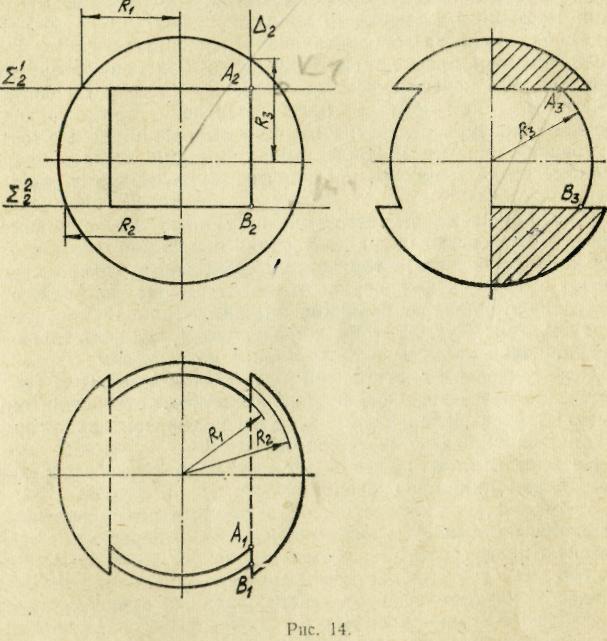
Рис. 14 показывает построение проекций контура призма­тического отверстия в шаре. Верхняя и нижняя стенки от­верстия, образованные горизонтальными плоскостями, пересекают сферическую поверхность по дугам окружностей, ви­димым в натуральную величину на горизонтальной проекции. Радиусы этих дуг, R₁ и R₂, определяются на фронтальной проекции, как радиусы окружностей в пересечении сфериче­ской поверхности с плоскостями Σ¹ и Σ², проведенными соот­ветственно через верхнюю и нижнюю стенки отверстия; они измеряются на следах Σ¹₂ и Σ²₂. Дуги на горизонтальной про­екции ограничиваются шириной отверстия.

На виде слева эти дуги будут проецироваться в отрезки прямых, как и на виде спереди.

Боковые стенки отверстия, образованные двумя профиль­ными плоскостями: и симметричной ей, — пересекают сфе­рическую поверхность по дугам одинакового радиуса R₃. Ра­венство радиусов вытекает из равенства удалений левой и правой стенок отверстия от центра шара (Радиус окружности в пересечении заданной сферы с плоскостью зависит только от расстояния между секущей плоскостью и центром сфе­ры; он равен радиусу сферы, если плоскость проходит через центр, и об­ращается в мюль, когда плоскость только касается сферы). Радиус R₃ изме­ряется на проекции плоскости . Дуги на вид слева проеци­руются в натуральную величину и сливаются попарно в одну дугу в силу симметрии. На виде сверху эти дуги проециру­ются в отрезки прямых, как лежащие в горизонтально-прое­цирующих (профильных) плоскостях.