VII. Построение проекций точек, расположенных на различных поверхностях

Часто, строя проекции предмета, можно сразу опреде­лить форму какого-либо элемента изображения, если его очертания состоят из прямых линий или окружностей. Но по­ложение такого элемента относительно остального изобра­жения или сами очертания элемента (когда они криволиней­ные) приходится определять по проекциям одной или не­скольких точек на поверхности предмета.

Общий метод определения точки на проекциях участка поверхности, несущей эту точку, состоит в следующем:

Через точку на поверхности проводят вспомогательную линию, проекции которой легко определяются на данной по­верхности.

На проекциях вспомогательной линии находят с по­мощью проекционной связи недостающую проекцию точки.

Вспомогательная линия должна быть простейшей для данной поверхности. Для плоскости это всегда отрезок пря­мой, опирающейся концами на края плоского участка или на ребра грани. Для поверхности вращения, если ось враще­ния перпендикулярна к одной из плоскостей проекций, мо­жет быть использована окружность, полученная в пересече­нии этой поверхности с плоскостью, перпендикулярной к оси вращения. Разумеется, вспомогательная плоскость прово­дится через рассматриваемую точку.

На конусе или цилиндре, в частности, также можно воспользоваться прямолинейной образующей.

Рассмотрим сказанное на примерах. На гранях пирами­ды, показанной на рис. 5, даны фронтальная проекция точки М и горизонтальная проекция точки. N. Найдем недостаю­щие проекции этих точек.

Через точку N проведем прямую 1—2, начав с ее фрон­тальной проекции 1₂—2₂. Найдя затем горизонтальную про­екцию 1₁—2₁, проведем вниз линию связи и отметим недо­стающую проекцию.

Для точки М был выбран отрезок, пересекающийся с бо­ковым ребром AD и нижним ребром АВ. Через ребро BD проводить вспомогательную прямую было бы нежелательно, так как BD — профильная прямая и проекцию точки на ней пришлось бы находить путем дополнительных построений, используя пропорциональное деление проекций отрезка про­екциями принадлежащей ему точки.

Для точки N, заданной своей горизонтальной проекцией N₁ используем вспомогательную прямую 3 — D, одним из концов которой будет вершина пирамиды. Построения будут такими же, как для точки М, но начнутся они с горизонталь­ной проекции.

На рис. 6 точки А задана своей фронтальной проекцией на поверхности сферы. Проведя через эту точку горизонталь­ную плоскость Σ (проекция Σ₂ проходит через А₂), получим в пересечении со сферой окружность, радиус г которой изме­ряется прямо на проекции Σ₂, как показано на чертеже. Са­ма окружность проецируется в натуральную величину на виде сверху. Проведя окружность, отмечаем на ней недоста­ющую проекцию А₁.

На рис. 7 показан усеченный конус, а точка К задана на горизонтальной проекции. Если бы через точку К была про­ведена плоскость, перпендикулярная оси конуса, она дала бы в пересечении с конусом окружность, проецирующуюся в на­туральную величину на виде сверху и проходящую через горизонтальную проекцию К. Проведем эту окружность, из­мерим ее радиус, и тогда несложно будет найти на фронталь­ной проекции уровень вспомогательной горизонтальной пло­скости, дающей в пересечении с конусом эту самую окружность. Отменив этот уровень, обозначим на нем недостаю­щую проекцию K₂ как показано на чертеже.

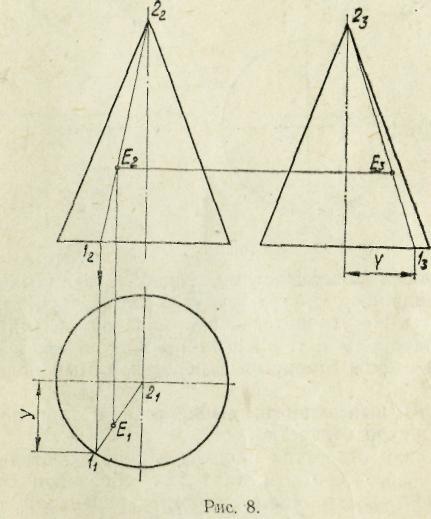
На рис. 8 и 9 показано, как строятся недостающие гори­зонтальная и профильная проекция точки Е на конусе и ци­линдре с помощью образующих (прямая 1—2 на обоих чер­тежах). Построения начинаются с фронтальной проекции об­разующей, проходящей через заданную фронтальную проек­цию точки Е. Затем строятся горизонтальная и профильная проекции образующей, а на них отмечаются одноименные проекции точки Е. Здесь следует обратить внимание, что про­фильные проекции указанной образующей и самой точки при наличии двух других проекций легко определяются без про­ведения внешних осей проекций (например, 1₃—2₃ на рис. 8 и Е₃ на рис. 9).